Diskussionspapier: Modell für Zeit und Raum
-
nicole6

- ModeratorIn

- Beiträge: 2333
- Registriert: 11.09.2009, 13:01
- Wohnort: München
- Ich bin: ehemalige SexarbeiterIn
Diskussionspapier: Modell für Zeit und Raum
Vor zwanzig Jahren schrieb ich eine Arbeit über ein alternatives Modell für
Zeit und Raum, und wollte es mit Physikprofessoren der Uni München
diskutieren. Aber alle Versuche schlugen fehl. Deshalb gab ich diese
Aktivität auf. Jetzt aber las ich das Buch von Unzicker über den Betrug
mit dem Higgs-Teilchen, und stellte fest, dass sich seither nichts geändert hat.
Es wird immer noch der gleich Unsinn geglaubt, obwohl das offizielle Bild,
das die Physik der Öffentlichkeit präsentiert, den eigenen Vorgaben widerspricht.
Jetzt entschloss ich mich, meine Theorie der bekanntesten Zeitschrift für Physik
zur Veröffentlichung anzubieten. Die Chance angenommen zu werden sind
sehr gering. Aber wenn ich es nicht einmal versuche, ist die Chance gleich Null.
Da besteht nur ein kleines Problem: falls meine Theorie wirklich angenommen
würde, dann würde das die ganzen bisherigen Theorien über den Haufen werfen!
Das was bisher als "Wahrheit" ausgegeben wird, müsste alles aufgegeben werden!
Meine Sorge hier ist, dass die Arbeit einfach abgelehnt wird, und danach
veröffentlich jemand meine Aussagen unter seinem Namen! Um dem vorzubeugen,
muss ich die Arbeit irgendwo niederlegen, wo man das Datum sehen kann, und wo
es Zeugen gibt, dass die Arbeit an dem Tag deponiert wurde. So kann ich dann
einem eventuellen Plagiatsversuch vorbeugen.
So kam mir die Idee, dass ich die Arbeit hier hochlade, wenn's recht ist.
Ich gehe nicht davon aus, dass der Inhalt irgend jemanden interessiert.
Aber es steht natürlich jeder frei sich einzulesen!
Ich kann nicht alles auf einmal hochladen, sondern in mehreren
Teilen, da ich die Arbeit umformatieren muss.
im folgenden Beitrag geht es los:
#############################################################
Zeit und Raum, und wollte es mit Physikprofessoren der Uni München
diskutieren. Aber alle Versuche schlugen fehl. Deshalb gab ich diese
Aktivität auf. Jetzt aber las ich das Buch von Unzicker über den Betrug
mit dem Higgs-Teilchen, und stellte fest, dass sich seither nichts geändert hat.
Es wird immer noch der gleich Unsinn geglaubt, obwohl das offizielle Bild,
das die Physik der Öffentlichkeit präsentiert, den eigenen Vorgaben widerspricht.
Jetzt entschloss ich mich, meine Theorie der bekanntesten Zeitschrift für Physik
zur Veröffentlichung anzubieten. Die Chance angenommen zu werden sind
sehr gering. Aber wenn ich es nicht einmal versuche, ist die Chance gleich Null.
Da besteht nur ein kleines Problem: falls meine Theorie wirklich angenommen
würde, dann würde das die ganzen bisherigen Theorien über den Haufen werfen!
Das was bisher als "Wahrheit" ausgegeben wird, müsste alles aufgegeben werden!
Meine Sorge hier ist, dass die Arbeit einfach abgelehnt wird, und danach
veröffentlich jemand meine Aussagen unter seinem Namen! Um dem vorzubeugen,
muss ich die Arbeit irgendwo niederlegen, wo man das Datum sehen kann, und wo
es Zeugen gibt, dass die Arbeit an dem Tag deponiert wurde. So kann ich dann
einem eventuellen Plagiatsversuch vorbeugen.
So kam mir die Idee, dass ich die Arbeit hier hochlade, wenn's recht ist.
Ich gehe nicht davon aus, dass der Inhalt irgend jemanden interessiert.
Aber es steht natürlich jeder frei sich einzulesen!
Ich kann nicht alles auf einmal hochladen, sondern in mehreren
Teilen, da ich die Arbeit umformatieren muss.
im folgenden Beitrag geht es los:
#############################################################
-
nicole6

- ModeratorIn

- Beiträge: 2333
- Registriert: 11.09.2009, 13:01
- Wohnort: München
- Ich bin: ehemalige SexarbeiterIn
RE: Diskussionspapier: Modell für Zeit und Raum
Diskussionspapier: Modell für Zeit und Raum
MODELL FÜR ZEIT UND RAUM
1. AXIOMATISCHE BASIS.
Der Ansatz hier ist wie folgt: 'Zeit' hat etwas mit Veränderung zu tun, mit 'Werden'. Selbst das mysteriöse 'Sein', von dem die Philosophen reden, kann von ihnen selbst nur im Bezug auf ihr eigenes Werden wahrgenommen werden. 'Sein' und 'Werden' sind keine Gegensätze, sondern sich ergänzende Komplementaritäten.
Die minimale Grundannahme als erstes Axiom sei:
Axiom 1: Es gibt Objekte die beobachtbar sind.
Für das zweite Axiom sind zwei Versionen angeboten, um sprachliche Mißverständnisse zu vermeiden. Die erste Formulierung ist
Axiom 2a: Objekte verändern sich
was in dem Sinne gemeint ist
Axiom 2b: Objekte erscheinen und werden durch andere ersetzt
Nun braucht man noch ein drittes Axiom, dessen Grundlage am Anfang dieses Jahrhunderts von POINCARÉ auf allgemeiner Ebene bewiesen wurde .
Axiom 3: Objekte ändern sich in Quanten
2. DEFINITION VON ‘ZEIT’.
Mit Hilfe der Axiome des vorherigen Abschnitts ist eine Definition von 'Zeit' möglich, die keinen Kreisschluß beinhaltet. In der Philosophie ist dies oft geschehen, wenn dabei auf den Begriff 'Bewegung' zurückgegriffen wurde. Dies ist nach Regeln der Logik natürlich unzulässig, da das zu Definierende in der Definition nicht schon vorausgesetzt werden darf.
Definition 1: "Zeit" ist die Lücke zwischen dem Erscheinen eines Objektes und dem Ersatz durch ein anderes.
Im Zusammenhang mit dieser Zeitdefinition läßt sich auch der komplementäre Begriff 'Dauer' definieren.
Ein Objekt ist demnach bei einer linearen Entwicklung durch zwei Zeitschritte eingerahmt und ein Zeitschritt durch zwei unterschiedliche Objekte von Dauer. Hier wird klar, daß 'Dauer' und 'Zeit' (von Philosophen oft mit 'Sein' und 'Werden' bezeichnet) keine Gegensätze sind, sondern komplementäre Aspekte eines Geschehens.
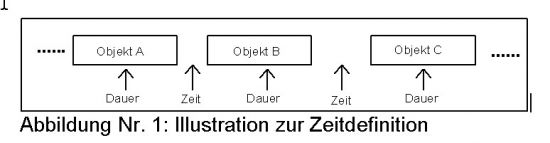
In Abbildung 1 ist illustriert, was man sich darunter vorstellen kann. Unter 'Objekt A' kann man alles einsetzen, was man als Zeitstruktur betrachten will. Ob es komplex ist oder einfach spielt keine Rolle. Wichtig ist nur, daß die Aspekte, deren Zeitablauf man untersuchen will, sich innerhalb des Bereiches, der mit 'Dauer' bezeichnet wird, nicht ändern.
3. GEOMETRISCHE MODELLE FÜR ZEIT.
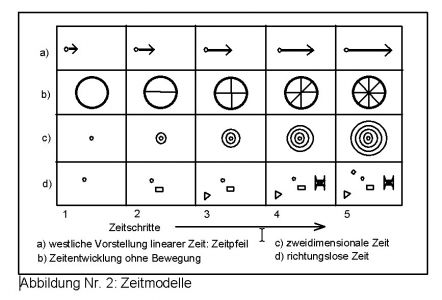
In westlichen Kulturen der Neuzeit wird zeitliche Entwicklung meist zuerst auf eine Gerade projiziert und dann im Nachhinein wird die Behauptung aufgestellt, die Zeit verlaufe linear, weil sie geradlinig sei (Abb. 2a). Das ist natürlich genauso unlogisch wie die Behauptung, daß zeitliche Entwicklung ohne Bewegung, d.h. ohne Ortsänderung, nicht möglich sei. Die Folge 2b zeigt das Gegenteil.
In Abbildung 2b wird der Kreis mit jedem Schritt weiter unterteilt. Dabei bewegt sich kein einziger Punkt des Kreises. Trotzdem ist das Objekt einer eindeutigen Veränderung unterworfen und eignet sich somit als Zählmechanismus für Zeiteinheiten. Innerhalb der Kreise von 2b findet man 'Dauer'. Dauer ist somit an Inhalt gebunden. Die Lücken zwischen den Schritten entsprechen der 'Zeit'. Etwas ähnliches kann man auch mit einer Kugel machen, die dann dementsprechend durch Ebenen geschnitten wird. In Abbildung 2c ist das Prinzip einer zweidimensionalen und in 2d einer richtungslosen Zeitausbreitung skizziert. Im letzten Fall wurden die Zeitschritte mit unterschiedlichen Symbolen gekennzeichnet.
4. ZUM BEGRIFF 'DIMENSION'
Der Begriff 'Dimension' wird verwendet, wenn man voneinander unabhängige Variable innerhalb eines Kontextes untersuchen und darstellen will. Allgemein gesehen, benötigt man zur Darstellung für jede unabhängige Größe eine separate Dimension.
Meist wird zur Darstellung von Dimensionen ein Koordinatensystem verwendet, bei dem die Achsen aufeinander senkrecht stehen. Die geometrische Darstellung von Unabhängigkeit ist der 90º Winkel. Algebraisch kann man es mit der Multiplikation von i machen, der Wurzel aus minus Eins.
Dimensionslos ist ein System, dessen Elemente zueinander in keiner zyklischen Beziehung stehen. Die Dimensionszahl läßt sich auch feststellen, indem man die kleinste Zahl an Elementen feststellt, mit denen sich das System durch zyklische Wiederholungen erzeugen läßt. Die Dimensionszahl kann dabei recht groß werden: "Man denke an die für verschiedene Spektralbereiche empfindlichen Stäbchen in der Retina oder an Untersuchungen der erstaunlichen Differentiation der Geruchszellen. Die Resultate legen nahe, daß der 'Geruchsraum' etwa so viele Dimensionen hat, wie es Sinneszellen im Riechepithelium gibt. Das geht in die Millionen."
5. ZEITRICHTUNG.
Es gibt theoretische Fälle, wo die Zeitrichtung keine Rolle spielt, wie z.B. in der klassischen Physik. Die Formeln sind zwar mathematisch klar und korrekt, aber auf die Realität bezogen falsch, genauso wie die Annahme der klassischen Physik von punktförmigen Körpern. "Es gibt nämlich den Punkt, das unendlich Kleine nicht. Ein wesentliches Merkmal der Newtonschen Mechanik ist die Differential- und Integralrechnung, die idealiter annimmt, daß etwas gegen Null geht und man deswegen Kurven oder Bahnen berechnen kann. Das geht aber nicht ganz genau. Auch in der makroskopischen Welt muß man sich immer für einen Standort entscheiden, der unter Umständen haarscharf neben dem Punkt liegt. Aber in einer dynamischen Theorie der Welt kann eben dies der Ausgangspunkt für viele Entwicklungen sein, die letzten Endes zu einer Störung oder zu einem Zusammenbruch des Systems führen, wenn dies hoch rückgekoppelt ist." .
"Ein Photon, das sich in der Zeit vorwärts bewegt, ist dasselbe wie ein Antiphoton, das sich in der Zeit rückwärts bewegt, doch da ein Antiphoton ein Photon ist, ist ein Photon, das sich in der Zeit vorwärts bewegt, dasselbe, wie ein Photon, das sich in der Zeit rückwärts bewegt." Teilchen und Antiteilchen unterscheiden sich durch die Zeitrichtung ihrer Existenz im Universum. Da Photonen ihre eigenen Antiteilchen sind, gibt es keine Zeit für sie; sie befinden sich außerhalb des Geschehens des dreidimensionalen Raumes, weshalb man im FEYNMAN-Diagramm bei Lichtteilchen die Zeitrichtung wegläßt.
6. DEFINITION VON PHASE.
Definition 3: 'Phase' ist die Übereinstimmung von Lücken bei simultanem Erscheinen von Objekten und dem Ersatz durch Andere.
7. ZEIT IN DER PHYSIK.
Wenn in Physikformeln die Größe 't' auftaucht, so sprechen die Forscher von 'Zeit'. Rein buchstabenmäßig ist es das gleiche Wort, welches man in der Alltagssprache verwendet. Doch inhaltlich unterscheiden sich die Begriffe. Die Größe 't' als Parameter steht nicht für den Ablauf der Ereignisse, sondern umfaßt das gesamte Geschehen. 'Zeit' im Alltag entspricht dem Ablaufen eines Kinofilms oder einer Videokassette im Fernsehen. Der Zeitparameter't' jedoch entspricht in diesem Beispiel der gesamten Filmrolle, oder der Videokassette, die auch im Regal stehen kann. Man kann sie vor- und zurückspulen, wiederholen und Einzelbilder schalten. Sie bleibt wie sie ist.
In manchen Büchern steht, daß die physikalische Zeit die vierte Dimension sei. Dies ist offensichtlich nicht richtig, denn sie erzeugt zwar eine höhere Dimension, wie Einsteins Formel t x c x i = x4 zeigt, aber sie ist es nicht. Die Größe i ist dimensionslos, c ist eine Geschwindigkeit und wird in Meter-pro-Sekunde gemessen und der Parameter t wird in Sekunden angegeben. Die Sekunden kürzen sich heraus und übrig bleibt Meter.
EINSTEINS Formel bezog sich auf die Konstruktion einer vierten Raumdimension. Geht man eine Stufe tiefer, so findet man in der Kinofilmprojektion ein Beispiel dafür. Bei Filmaufnahmen werden Ereignisse (xe) durch ein Aufnahmeobjektiv in der Zeit (t) in konstanten Einheiten (k) (Quanten) auf einen Film projiziert. Die Wurzel aus minus Eins (i) erzeugt algebraisch eine neue Dimension und bedeutet den rechten Winkel zwischen dem Licht der Ereignisfolgen und dem Film als Objekt verräumlichter Zeit.
Bei der Projektion im Kino geschieht das Umgekehrte. Hier wird der gequantelte (zweidimensionale) Raum (xe) mit Hilfe von konstanten Phasenschüben (k) in der Zeit (t) im rechten Winkel (i) am Projektionsobjektiv vorbeigeführt und die Zuschauer haben dadurch den Eindruck von bewegtem Geschehen.
In der Physik trennt eine Nullgegenwart als scharfe Grenze Vergangenheit und Zukunft voneinander. Beim Menschen ist der Übergang von Zukunft zu Gegenwartsbewußtsein zu Vergangenheit ausgedehnt und fließend. Entfernt man bei Personen durch Hypnose die ausgedehnte Gegenwart, fallen sie in schizophrenes Verhalten, werden aggressiv und haben Todesgefühle .
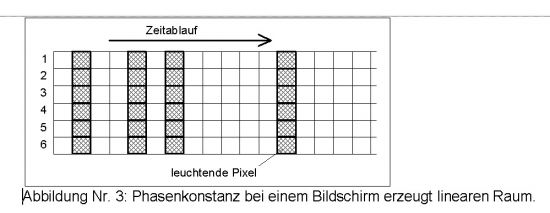
8. PRINZIP DER ERZEUGUNG VON RAUM-DIMENSIONEN.
Man geht von einem Energiesystem aus, zum Beispiel die Bildröhre eines Fernsehers, bei dem diskrete Energieeinheiten beliebig aktiviert werden können. Will man einen einzigen Punkt (die 'Nullte' Dimension) auf dem Bildschirm erzeugen, so muß nach konstanten Zeitabschnitten die Energie aktiviert werden. Die Zeit erweist sich somit als grundlegendere Einheit als der Raum, der von ihr abgeleitet ist . Da der Raum von der Zeit abgeleitet und die Zeit diskret ist, muß auch der Raum aus diskreten Elementen aufgebaut sein, wie winzig sie auch sein mögen. RICHARD FEYNMANs Einstellung dazu ist ähnlich: "Ich glaube, daß die Theorie von kontinuierlichem Raum falsch ist, weil wir diese Unendlichkeiten und andere Schwierigkeiten bekommen, und wir stehen mit der Frage da, was die Größe der Partikel bestimmt. Ich vermute eher, daß die simplen Ideen der Geometrie, auf unendlich kleine Bereiche ausgedehnt, falsch sind."
Um ein Linie zu erzeugen, muß dieser Vorgang mit einer zusätzlichen Phase wiederholt werden. Diese zweite Phase ist von der ersten unabhängig. Die Lage der erzeugten Geraden wird von der gewählten Konstanten bestimmt. Mathematisch gesehen, wird die Zeit t zur Erzeugung gleicher Zeitabstände mit einer Konstanten k multipliziert und einem Faktor i, der Unabhängigkeit garantiert. In einer geometrischen Darstellung liegt die unabhängige Größe rechtwinklig zur abhängigen. Sie bilden zusammen das allseits bekannte Koordinatenkreuz mit x- und y-Achse. Algebraisch benutzt man die imaginäre Grösse 'i'. Zusammengefaßt erhält man:
t x k x i
Setzt man für die Konstante k die 'Lichtgeschwindigkeit' c, so erhält man die EINSTEIN-MINKOWSKI Formel zur Erzeugung einer höheren Raumdimension auf der Basis einer gegebenen Zeitabfolge: t x c x i .
Aufgrund historischen Gegebenheiten hat sich die Konvention eingebürgert, einer Linie die Dimension '1' zuzuschreiben. Aber wie EINSTEIN richtig bemerkte, läßt sich die Linie aus der nächst niederen Dimension des Punktes mit Hilfe der Zeit herstellen:
"Betrachten wir z.B. einen beliebig bewegten materiellen Punkt! Hätte derselbe nur eine momentane Existenz ohne Dauer, so wäre er raumzeitlich beschrieben durch ein einziges Wertesystem x1, x2, x3, x4. Seine bleibende Existenz ist also durch eine unendlich große Zahl von solchen Wertsystemen charakterisiert, deren Koordinatenwerte sich stetig aneinanderreihen; dem Massenpunkte entspricht also eine (eindimensionale) Linie im vierdimensionalen Kontinuum."
EINSTEIN führte hier offensichtlich eine zweite Zeitachse ein. Die erste ist die Zeit in welcher der Punkt existiert, um Dauer zu haben. Die zweite ist dann die Zeit, in der dieser Punkt seine Bewegung vollführt. Diese Zeiten müssen voneinander unabhängig sein, sonst würde der Punkt bei einem Halt verschwinden, wenn mit der Bewegungszeit auch die Existenzzeit gekoppelt wäre.
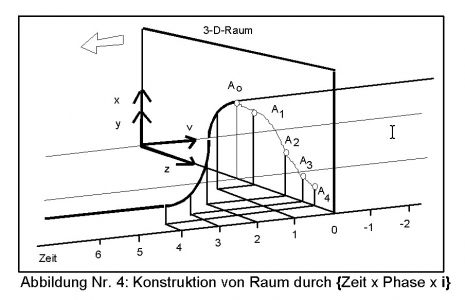
Zur Visualisierung dient die Abb.4. Zur Darstellung von vier Dimensionen in einem Diagramm, wurden drei Raumdimensionen zu einer Ebene zusammen geschoben. Die x-y-Ebene wird durch die Vertikale abgekürzt, die z-Richtung bleibt erhalten. Die v-Achse ist nun die Zeit. Betrachten wir nun einen Punkt A0, der bis zum Zeitpunkt t0 ruhen soll. Dadurch beschreibt er in v-Richtung eine Gerade. Ab dem Zeitpunkt t0 soll sich der Punkt über A1 bis A4 bewegen, und dann wieder ruhen. Dadurch entsteht, wie man aus der Skizze entnehmen kann, eine gekrümmte Kurve, die dann wieder in eine Gerade übergeht. Man kann es aber auch umgekehrt betrachten. Jetzt sei die Linie stillstehend und die Raum-'Ebene' bewegt sich in Richtung des weißen Pfeiles. Dann haben wir an den Schnittstellen den gleichen Effekt wie vorher.
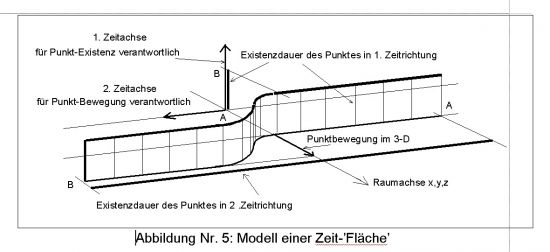
In Abb.4 kann man nur eine Zeitachse eintragen, weil die Raum-'Fläche' die beiden anderen wegnimmt. Faßt man aber alle drei Raumachsen zu einer zusammen, so ergibt sich ein Bild wie in Abb.5. Die Kurve, die der Punkt A in der höheren Dimension einnimmt, wird nun auf die Grundfläche projiziert. Die Zeitachse für die Existenz des Punktes muß auf allen anderen senkrecht stehen und zeigt demnach nach oben. Die 'Existenz an sich' bildet sich mit der ersten Zeitachse als stehendes Band ab. In dieser Darstellung sind die Zeitskalen auf den Zeitachsen 1 und 2 unterschiedlich. Beide Zeitachsen erzeugen zwischen den Punkten A und B die Zeitfläche. Die Punktbewegung im 3-D formt die Kurve ins Band.
EINSTEIN machte den Schritt in eine höhere Dimension vom dreidimensionalen Raum aus. Aber dieselbe Logik läßt sich auch schon von unten her anwenden. In einem mehrdimensionalen Energiesystem, wie es von J.A.WHEELER vorgeschlagen wurde, bedarf es einer gewissen Zahl an Energieschwingungen in Phase, damit die Energie sich zu etwas Materiellem 'kondensiert'. Wenn die Übereinstimmungen der Phasen verschwinden, löst sich das Objekt wieder auf.
Die Abstände zwischen den Zeitschritten wurden ungleichmäßig gewählt, um zu zeigen, daß es nicht auf die Darstellungsweise ankommt. In kurzen Stichworten zusammengefaßt ergibt sich also:
1. Zeitdimension: Veränderungen allgemeiner Art (siehe Zeitdefinition).
2. Zeitdimension: Veränderungen von 1.) sind in Phase: ein Punkt entsteht.
3. Zeitdimension: Veränderungen von 2.) sind in Phase: der Punkt erzeugt eine Linie.
4. Zeitdimension: Veränderungen von 3.) sind in Phase: die Linie erzeugt eine Fläche.
5. Zeitdimension: Veränderungen von 4.) sind in Phase: die Fläche erzeugt den Raum.
Tabelle Nr. 1: Zeitdimensionen
MODELL FÜR ZEIT UND RAUM
1. AXIOMATISCHE BASIS.
Der Ansatz hier ist wie folgt: 'Zeit' hat etwas mit Veränderung zu tun, mit 'Werden'. Selbst das mysteriöse 'Sein', von dem die Philosophen reden, kann von ihnen selbst nur im Bezug auf ihr eigenes Werden wahrgenommen werden. 'Sein' und 'Werden' sind keine Gegensätze, sondern sich ergänzende Komplementaritäten.
Die minimale Grundannahme als erstes Axiom sei:
Axiom 1: Es gibt Objekte die beobachtbar sind.
Für das zweite Axiom sind zwei Versionen angeboten, um sprachliche Mißverständnisse zu vermeiden. Die erste Formulierung ist
Axiom 2a: Objekte verändern sich
was in dem Sinne gemeint ist
Axiom 2b: Objekte erscheinen und werden durch andere ersetzt
Nun braucht man noch ein drittes Axiom, dessen Grundlage am Anfang dieses Jahrhunderts von POINCARÉ auf allgemeiner Ebene bewiesen wurde .
Axiom 3: Objekte ändern sich in Quanten
2. DEFINITION VON ‘ZEIT’.
Mit Hilfe der Axiome des vorherigen Abschnitts ist eine Definition von 'Zeit' möglich, die keinen Kreisschluß beinhaltet. In der Philosophie ist dies oft geschehen, wenn dabei auf den Begriff 'Bewegung' zurückgegriffen wurde. Dies ist nach Regeln der Logik natürlich unzulässig, da das zu Definierende in der Definition nicht schon vorausgesetzt werden darf.
Definition 1: "Zeit" ist die Lücke zwischen dem Erscheinen eines Objektes und dem Ersatz durch ein anderes.
Im Zusammenhang mit dieser Zeitdefinition läßt sich auch der komplementäre Begriff 'Dauer' definieren.
Ein Objekt ist demnach bei einer linearen Entwicklung durch zwei Zeitschritte eingerahmt und ein Zeitschritt durch zwei unterschiedliche Objekte von Dauer. Hier wird klar, daß 'Dauer' und 'Zeit' (von Philosophen oft mit 'Sein' und 'Werden' bezeichnet) keine Gegensätze sind, sondern komplementäre Aspekte eines Geschehens.
In Abbildung 1 ist illustriert, was man sich darunter vorstellen kann. Unter 'Objekt A' kann man alles einsetzen, was man als Zeitstruktur betrachten will. Ob es komplex ist oder einfach spielt keine Rolle. Wichtig ist nur, daß die Aspekte, deren Zeitablauf man untersuchen will, sich innerhalb des Bereiches, der mit 'Dauer' bezeichnet wird, nicht ändern.

3. GEOMETRISCHE MODELLE FÜR ZEIT.
In westlichen Kulturen der Neuzeit wird zeitliche Entwicklung meist zuerst auf eine Gerade projiziert und dann im Nachhinein wird die Behauptung aufgestellt, die Zeit verlaufe linear, weil sie geradlinig sei (Abb. 2a). Das ist natürlich genauso unlogisch wie die Behauptung, daß zeitliche Entwicklung ohne Bewegung, d.h. ohne Ortsänderung, nicht möglich sei. Die Folge 2b zeigt das Gegenteil.
In Abbildung 2b wird der Kreis mit jedem Schritt weiter unterteilt. Dabei bewegt sich kein einziger Punkt des Kreises. Trotzdem ist das Objekt einer eindeutigen Veränderung unterworfen und eignet sich somit als Zählmechanismus für Zeiteinheiten. Innerhalb der Kreise von 2b findet man 'Dauer'. Dauer ist somit an Inhalt gebunden. Die Lücken zwischen den Schritten entsprechen der 'Zeit'. Etwas ähnliches kann man auch mit einer Kugel machen, die dann dementsprechend durch Ebenen geschnitten wird. In Abbildung 2c ist das Prinzip einer zweidimensionalen und in 2d einer richtungslosen Zeitausbreitung skizziert. Im letzten Fall wurden die Zeitschritte mit unterschiedlichen Symbolen gekennzeichnet.

4. ZUM BEGRIFF 'DIMENSION'
Der Begriff 'Dimension' wird verwendet, wenn man voneinander unabhängige Variable innerhalb eines Kontextes untersuchen und darstellen will. Allgemein gesehen, benötigt man zur Darstellung für jede unabhängige Größe eine separate Dimension.
Meist wird zur Darstellung von Dimensionen ein Koordinatensystem verwendet, bei dem die Achsen aufeinander senkrecht stehen. Die geometrische Darstellung von Unabhängigkeit ist der 90º Winkel. Algebraisch kann man es mit der Multiplikation von i machen, der Wurzel aus minus Eins.
Dimensionslos ist ein System, dessen Elemente zueinander in keiner zyklischen Beziehung stehen. Die Dimensionszahl läßt sich auch feststellen, indem man die kleinste Zahl an Elementen feststellt, mit denen sich das System durch zyklische Wiederholungen erzeugen läßt. Die Dimensionszahl kann dabei recht groß werden: "Man denke an die für verschiedene Spektralbereiche empfindlichen Stäbchen in der Retina oder an Untersuchungen der erstaunlichen Differentiation der Geruchszellen. Die Resultate legen nahe, daß der 'Geruchsraum' etwa so viele Dimensionen hat, wie es Sinneszellen im Riechepithelium gibt. Das geht in die Millionen."
5. ZEITRICHTUNG.
Es gibt theoretische Fälle, wo die Zeitrichtung keine Rolle spielt, wie z.B. in der klassischen Physik. Die Formeln sind zwar mathematisch klar und korrekt, aber auf die Realität bezogen falsch, genauso wie die Annahme der klassischen Physik von punktförmigen Körpern. "Es gibt nämlich den Punkt, das unendlich Kleine nicht. Ein wesentliches Merkmal der Newtonschen Mechanik ist die Differential- und Integralrechnung, die idealiter annimmt, daß etwas gegen Null geht und man deswegen Kurven oder Bahnen berechnen kann. Das geht aber nicht ganz genau. Auch in der makroskopischen Welt muß man sich immer für einen Standort entscheiden, der unter Umständen haarscharf neben dem Punkt liegt. Aber in einer dynamischen Theorie der Welt kann eben dies der Ausgangspunkt für viele Entwicklungen sein, die letzten Endes zu einer Störung oder zu einem Zusammenbruch des Systems führen, wenn dies hoch rückgekoppelt ist." .
"Ein Photon, das sich in der Zeit vorwärts bewegt, ist dasselbe wie ein Antiphoton, das sich in der Zeit rückwärts bewegt, doch da ein Antiphoton ein Photon ist, ist ein Photon, das sich in der Zeit vorwärts bewegt, dasselbe, wie ein Photon, das sich in der Zeit rückwärts bewegt." Teilchen und Antiteilchen unterscheiden sich durch die Zeitrichtung ihrer Existenz im Universum. Da Photonen ihre eigenen Antiteilchen sind, gibt es keine Zeit für sie; sie befinden sich außerhalb des Geschehens des dreidimensionalen Raumes, weshalb man im FEYNMAN-Diagramm bei Lichtteilchen die Zeitrichtung wegläßt.
6. DEFINITION VON PHASE.
Definition 3: 'Phase' ist die Übereinstimmung von Lücken bei simultanem Erscheinen von Objekten und dem Ersatz durch Andere.

7. ZEIT IN DER PHYSIK.
Wenn in Physikformeln die Größe 't' auftaucht, so sprechen die Forscher von 'Zeit'. Rein buchstabenmäßig ist es das gleiche Wort, welches man in der Alltagssprache verwendet. Doch inhaltlich unterscheiden sich die Begriffe. Die Größe 't' als Parameter steht nicht für den Ablauf der Ereignisse, sondern umfaßt das gesamte Geschehen. 'Zeit' im Alltag entspricht dem Ablaufen eines Kinofilms oder einer Videokassette im Fernsehen. Der Zeitparameter't' jedoch entspricht in diesem Beispiel der gesamten Filmrolle, oder der Videokassette, die auch im Regal stehen kann. Man kann sie vor- und zurückspulen, wiederholen und Einzelbilder schalten. Sie bleibt wie sie ist.
In manchen Büchern steht, daß die physikalische Zeit die vierte Dimension sei. Dies ist offensichtlich nicht richtig, denn sie erzeugt zwar eine höhere Dimension, wie Einsteins Formel t x c x i = x4 zeigt, aber sie ist es nicht. Die Größe i ist dimensionslos, c ist eine Geschwindigkeit und wird in Meter-pro-Sekunde gemessen und der Parameter t wird in Sekunden angegeben. Die Sekunden kürzen sich heraus und übrig bleibt Meter.
EINSTEINS Formel bezog sich auf die Konstruktion einer vierten Raumdimension. Geht man eine Stufe tiefer, so findet man in der Kinofilmprojektion ein Beispiel dafür. Bei Filmaufnahmen werden Ereignisse (xe) durch ein Aufnahmeobjektiv in der Zeit (t) in konstanten Einheiten (k) (Quanten) auf einen Film projiziert. Die Wurzel aus minus Eins (i) erzeugt algebraisch eine neue Dimension und bedeutet den rechten Winkel zwischen dem Licht der Ereignisfolgen und dem Film als Objekt verräumlichter Zeit.
Bei der Projektion im Kino geschieht das Umgekehrte. Hier wird der gequantelte (zweidimensionale) Raum (xe) mit Hilfe von konstanten Phasenschüben (k) in der Zeit (t) im rechten Winkel (i) am Projektionsobjektiv vorbeigeführt und die Zuschauer haben dadurch den Eindruck von bewegtem Geschehen.
In der Physik trennt eine Nullgegenwart als scharfe Grenze Vergangenheit und Zukunft voneinander. Beim Menschen ist der Übergang von Zukunft zu Gegenwartsbewußtsein zu Vergangenheit ausgedehnt und fließend. Entfernt man bei Personen durch Hypnose die ausgedehnte Gegenwart, fallen sie in schizophrenes Verhalten, werden aggressiv und haben Todesgefühle .
8. PRINZIP DER ERZEUGUNG VON RAUM-DIMENSIONEN.
Man geht von einem Energiesystem aus, zum Beispiel die Bildröhre eines Fernsehers, bei dem diskrete Energieeinheiten beliebig aktiviert werden können. Will man einen einzigen Punkt (die 'Nullte' Dimension) auf dem Bildschirm erzeugen, so muß nach konstanten Zeitabschnitten die Energie aktiviert werden. Die Zeit erweist sich somit als grundlegendere Einheit als der Raum, der von ihr abgeleitet ist . Da der Raum von der Zeit abgeleitet und die Zeit diskret ist, muß auch der Raum aus diskreten Elementen aufgebaut sein, wie winzig sie auch sein mögen. RICHARD FEYNMANs Einstellung dazu ist ähnlich: "Ich glaube, daß die Theorie von kontinuierlichem Raum falsch ist, weil wir diese Unendlichkeiten und andere Schwierigkeiten bekommen, und wir stehen mit der Frage da, was die Größe der Partikel bestimmt. Ich vermute eher, daß die simplen Ideen der Geometrie, auf unendlich kleine Bereiche ausgedehnt, falsch sind."
Um ein Linie zu erzeugen, muß dieser Vorgang mit einer zusätzlichen Phase wiederholt werden. Diese zweite Phase ist von der ersten unabhängig. Die Lage der erzeugten Geraden wird von der gewählten Konstanten bestimmt. Mathematisch gesehen, wird die Zeit t zur Erzeugung gleicher Zeitabstände mit einer Konstanten k multipliziert und einem Faktor i, der Unabhängigkeit garantiert. In einer geometrischen Darstellung liegt die unabhängige Größe rechtwinklig zur abhängigen. Sie bilden zusammen das allseits bekannte Koordinatenkreuz mit x- und y-Achse. Algebraisch benutzt man die imaginäre Grösse 'i'. Zusammengefaßt erhält man:
t x k x i
Setzt man für die Konstante k die 'Lichtgeschwindigkeit' c, so erhält man die EINSTEIN-MINKOWSKI Formel zur Erzeugung einer höheren Raumdimension auf der Basis einer gegebenen Zeitabfolge: t x c x i .
Aufgrund historischen Gegebenheiten hat sich die Konvention eingebürgert, einer Linie die Dimension '1' zuzuschreiben. Aber wie EINSTEIN richtig bemerkte, läßt sich die Linie aus der nächst niederen Dimension des Punktes mit Hilfe der Zeit herstellen:
"Betrachten wir z.B. einen beliebig bewegten materiellen Punkt! Hätte derselbe nur eine momentane Existenz ohne Dauer, so wäre er raumzeitlich beschrieben durch ein einziges Wertesystem x1, x2, x3, x4. Seine bleibende Existenz ist also durch eine unendlich große Zahl von solchen Wertsystemen charakterisiert, deren Koordinatenwerte sich stetig aneinanderreihen; dem Massenpunkte entspricht also eine (eindimensionale) Linie im vierdimensionalen Kontinuum."
EINSTEIN führte hier offensichtlich eine zweite Zeitachse ein. Die erste ist die Zeit in welcher der Punkt existiert, um Dauer zu haben. Die zweite ist dann die Zeit, in der dieser Punkt seine Bewegung vollführt. Diese Zeiten müssen voneinander unabhängig sein, sonst würde der Punkt bei einem Halt verschwinden, wenn mit der Bewegungszeit auch die Existenzzeit gekoppelt wäre.

Zur Visualisierung dient die Abb.4. Zur Darstellung von vier Dimensionen in einem Diagramm, wurden drei Raumdimensionen zu einer Ebene zusammen geschoben. Die x-y-Ebene wird durch die Vertikale abgekürzt, die z-Richtung bleibt erhalten. Die v-Achse ist nun die Zeit. Betrachten wir nun einen Punkt A0, der bis zum Zeitpunkt t0 ruhen soll. Dadurch beschreibt er in v-Richtung eine Gerade. Ab dem Zeitpunkt t0 soll sich der Punkt über A1 bis A4 bewegen, und dann wieder ruhen. Dadurch entsteht, wie man aus der Skizze entnehmen kann, eine gekrümmte Kurve, die dann wieder in eine Gerade übergeht. Man kann es aber auch umgekehrt betrachten. Jetzt sei die Linie stillstehend und die Raum-'Ebene' bewegt sich in Richtung des weißen Pfeiles. Dann haben wir an den Schnittstellen den gleichen Effekt wie vorher.
In Abb.4 kann man nur eine Zeitachse eintragen, weil die Raum-'Fläche' die beiden anderen wegnimmt. Faßt man aber alle drei Raumachsen zu einer zusammen, so ergibt sich ein Bild wie in Abb.5. Die Kurve, die der Punkt A in der höheren Dimension einnimmt, wird nun auf die Grundfläche projiziert. Die Zeitachse für die Existenz des Punktes muß auf allen anderen senkrecht stehen und zeigt demnach nach oben. Die 'Existenz an sich' bildet sich mit der ersten Zeitachse als stehendes Band ab. In dieser Darstellung sind die Zeitskalen auf den Zeitachsen 1 und 2 unterschiedlich. Beide Zeitachsen erzeugen zwischen den Punkten A und B die Zeitfläche. Die Punktbewegung im 3-D formt die Kurve ins Band.

EINSTEIN machte den Schritt in eine höhere Dimension vom dreidimensionalen Raum aus. Aber dieselbe Logik läßt sich auch schon von unten her anwenden. In einem mehrdimensionalen Energiesystem, wie es von J.A.WHEELER vorgeschlagen wurde, bedarf es einer gewissen Zahl an Energieschwingungen in Phase, damit die Energie sich zu etwas Materiellem 'kondensiert'. Wenn die Übereinstimmungen der Phasen verschwinden, löst sich das Objekt wieder auf.

Die Abstände zwischen den Zeitschritten wurden ungleichmäßig gewählt, um zu zeigen, daß es nicht auf die Darstellungsweise ankommt. In kurzen Stichworten zusammengefaßt ergibt sich also:
1. Zeitdimension: Veränderungen allgemeiner Art (siehe Zeitdefinition).
2. Zeitdimension: Veränderungen von 1.) sind in Phase: ein Punkt entsteht.
3. Zeitdimension: Veränderungen von 2.) sind in Phase: der Punkt erzeugt eine Linie.
4. Zeitdimension: Veränderungen von 3.) sind in Phase: die Linie erzeugt eine Fläche.
5. Zeitdimension: Veränderungen von 4.) sind in Phase: die Fläche erzeugt den Raum.
Tabelle Nr. 1: Zeitdimensionen
-
nicole6

- ModeratorIn

- Beiträge: 2333
- Registriert: 11.09.2009, 13:01
- Wohnort: München
- Ich bin: ehemalige SexarbeiterIn
RE: Diskussionspapier: Modell für Zeit und Raum
Der nulldimensionale Raum 0-D
Die Eigenschaften des Punktes werden in Raumkonstruktionen meist vernachlässigt. Es mag sein, daß sich hier psychologische Wertungen einschleichen, die dem Punkt etwas 'niederes' und 'wertloses' zuschreiben.
Wie wir oben sahen, muß Energie mit sich selbst in Phase sein, um selbst in einem dimensionslosen Feld eine Punktdimension zu konstituieren. 'Phase' ist aber eine Existenzdimension der Punktdimension und kann z.B. geometrisch dargestellt werden. Für eine endlose Existenz dieser Punktdimension 0-D muß der Algorithmus 'Phase' beliebig oft angewendet werden können. Diese Phasenentwicklung kann man als Gerade darstellen, solange man sich bewußt bleibt, daß es keine Raumgerade ist! Das eine Ende dieser Phasengeraden ist der nulldimensionale Raum 0-D. Unter dieser Annahme macht es Sinn zu fragen wie ein gekrümmter 0-D aussieht.
Allgemein wird zur Konstruktion gekrümmter Räume eine zweite Phasenentwicklung angenommen, die von der ersten unabhängig ist, graphisch wird sie also rechtwinklig zur ersten Phase aufgetragen.
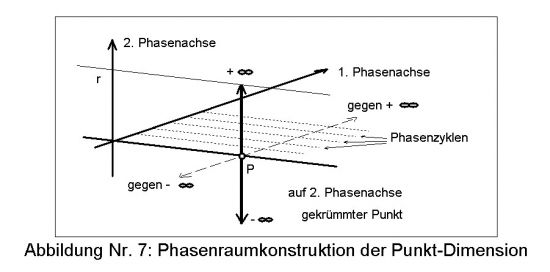
Die graphische Darstellung von Abb. 7 soll keinen 3-D-Raum postulieren in dem der Punkt erscheint. Diese visuelle Präsentation der Konstruktion wurde gewählt, weil sie einfacher nachzuvollziehen ist, als der rein algebraische Weg. Die Existenz des Punktes P ist durch die Phasenzyklen der ersten Phasenachse gesichert. Postuliert man eine zweite Phasenachse, so kann man auf ihr die Entwicklung der ersten komprimiert darstellen, was der Krümmung des Punktes in sich selbst entspricht. Der Abstand der Komprimierung ist in Abb. 7 mit r angegeben, auf den Plus-Unendlich projiziert wird und in der anderen Richtung entsprechend die Minuswerte der negativen Zyklen. Der gekrümmte Punkt erscheint als Phasen-Strecke, unterscheidet sich von einer normalen Strecke allerdings durch die Unendlichwerte an den Enden und dem Nullpunkt in der Mitte. Eine normale Strecke auf einer eindimensionalen Geraden ist 'ein Objekt im Raum', wogegen die obige Konstruktion 'einen gekrümmten Raum' herstellt. Dieser Unterschied wird noch mehrfach in den höheren Dimensionen auftauchen. Hier wird auch die Differenz zwischen dem Punkt als 'Dimension' und als 'Objekt' klar. Die Punktdimension braucht keine höheren Strecken-Räume zur Existenz, ein Punktobjekt aber schon.
Der eindimensionale Raum 1-D.
Die Dimension der Linie kann als Objekte Punkte oder Strecken enthalten. In der Regel wird zur Skalierung eine Metrik darauf angewendet, die nach beiden Seiten beliebige Werte annehmen kann. Sieht man eine Gerade nicht nur als Linie an, sondern auch als eindimensionalen Raum, so kann man untersuchen, was bei einer Raumkrümmung des 1-D geschieht; Voraussetzung der Krümmung ist die Einbettung in einen 2-D. In der Mathematik wird oft behauptet, daß die Krümmung auch ohne Einbettung in einen höher dimensionalen Raum gehe. Doch wenn man genau hinschaut was gemacht wird, so erkennt man, daß kein gekrümmter Raum erzeugt wird, sondern ein gekrümmtes Objekt im Raum. Der Unterschied wird im Folgenden deutlich.

Abbildung 8a zeigt die übliche Darstellung des eindimensionalen Raumes (1-D) mit dem Nullpunkt und den beiden Richtungen plus und minus Unendlich, meist nach links und rechts orientiert. Um den 1-D zu krümmen, muß er in einere höhere Dimension eingebettet sein, in den 2-D. Dann kann man 2 Seiten des 1-D feststellen und sie beispielsweise mit plus und minus-Seite benennen. Die plus-Seite wurde in der Abbildung schraffiert, um deutlich zu machen, was bei der Krümmung geschieht. Sie ist auf 2 Weisen möglich, einmal zur plus-Seite hin (b) und einmal nach Minus (c). Der Unendlich-'Punkt' liegt dann irgendwo gegenüber des Nullpunktes, abhängig davon, welche Skalierung man benutzt. Ist sie symmetrisch, liegt Unendlich im 180* Winkel zum Nullpunkt.

Oft wird bei der Darstellung gekrümmter Räume gepfuscht und es wird nicht nur ‘Unendlich’ einfach weggelassen, sondern auch die zweite Krümmung. Dadurch allerdings wird aus der eindimensionalen gekrümmten Dimension ein einfaches gekrümmtes Objekt. Doch es besteht ein fundamentaler Unterschied zwischen
a) gekrümmten Objekten im Raum und
b) gekrümmtem Raum.
Im obigen Beispiel fällt unter a) der Kreis und unter b) der gekrümmte 1-D. Die offensichtlichste Differenz ist die doppelte Existenz des gekrümmten 1-D. Die Darstellungen Abb. 8b und 8c haben unterschiedliche Parität. Geht man in b) vom Nullpunkt aus im Uhrzeigersinn der Linie entlang, bewegt man sich nach minus Unendlich, in c aber nach plus Unendlich! Im Gegenuhrzeigersinn ist es umgekehrt. Ein Kreis dagegen hat keine Parität und alle Punkte auf dem Kreis sind gleichwertig, was im Falle des gekrümmten 1-D nicht der Fall ist.
Angenommen, es gäbe eindimensionale Wesen, wie könnten sie höherdimensionale Objekte erkennen? Als Objekte sind für sie nur Punkte und Strecken erkennbar. Somit würde die Projektion eines Rechtecks parallel zur x-Achse die gleiche Strecke B ergeben, wie die Strecke A in Abb. 9. Doch das ändert sich, wenn das Rechteck gedreht wird. Dann verlängert sich die Strecke und hat innere Endpunkte. Die vorher parallele Seiten erscheinen als C und D. In der Abbildung wurden sie zur Verdeutlichung ein wenig seitlich verschoben. Ein Kreisschnitt mit dem 1-D ergibt zwei Punkte.
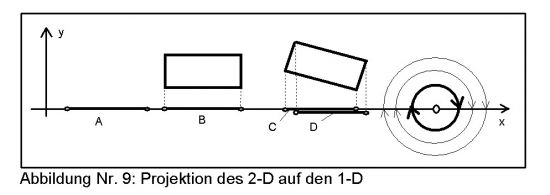
Dreht man den Kreis, so bekommen die Schnittpunkte eine zusätzliche Eigenschaft der Gerichtetheit, die zwar nicht direkt im 1-D erkennbar ist, die aber indirekt gewisse Auswirkungen zeigt. Die Ausrichtung der beiden Schnittpunkte ist entweder */* oder */* oder Null/Null. Was nicht möglich ist, sind die Kombinationen */* und */*. Wenn die 1-D-Wesen die Möglichkeit hätten die Ausrichtung zu ändern, dann könnten sie aus ihrer Sicht eine 'Fernwirkung' erfahren. Wenn sie die Richtung der einen Seite von * auf * ändern, wechselt der andere Punkt ebenfalls seine Ausrichtung. Die Verbundenheit der Punkte würde sich auch dadurch zeigen, daß diese Eigenschaft erhalten bleibt, selbst wenn sich die Punkte voneinander entfernen.
Der zweidimensionale Raum 2-D
Um die unterschiedlich verwendeten Begriffe 'Fläche', 'Ebene' und 'Zweidimensionaler Raum' auseinanderzuhalten, treffen wir folgende Konvention: 'Zweidimensionaler Raum' ist der Oberbegriff und umschließt auch nicht-euklidische Konstruktionen. Abgekürzt steht dafür 2-D-Raum, oder wenn es klar ist, daß 'Raum' gemeint ist und nicht 'Zeit', auch nur 2-D. Ein Teilbereich davon sei eine 'Fläche', z.B. eine Oberfläche und wenn sie plan ist, soll sie 'Ebene' heißen.
In Abb. 10a ist ein 2-D mit den beiden Achsen x und y skizziert. Zur Raumkrümmung des 2-D bedarf es einer Einbettung in den 3-D. Man beginnt beispielsweise mit der Krümmung um die y-Achse und erhält die Form einer Röhre (Abb. 10b). Was geschieht dabei mit Unendlich von y? Es kann ja nicht verschwinden, sonst ist es kein gekrümmter 2-D-Raum mehr, sondern nur noch ein gekrümmtes 3-D-Objekt im 3-D-Raum.
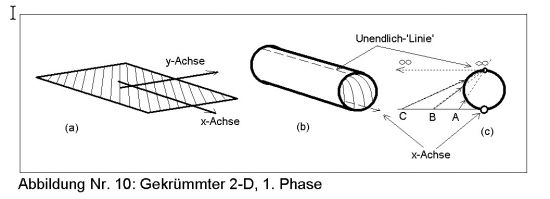
Unendlich von y bildet auf der Gegenseite der x-Achse eine Linie. Für die Skalierung der Werte dazwischen bietet sich eine Methode an, die der RIEMANNschen Zahlenkugel verwandt ist. Zieht man von der Unendlich-Linie zur ursprünglichen x/y-Ebene Geraden, so schneiden diese das Rohr an bestimmten Stellen. Auf diese Schnittpunkte werden alle Ebenenpunkte projiziert. In c sind die Punkte A, B, und C als Beispiel gegeben. Bezeichnet man die obere schraffierte Seite der Fläche mit '+', dann kommt in diesem Fall die Plusseite nach innen und die unschraffierte nach außen. Biegt man die Fläche nach unten, so zeigt die schraffierte Fläche nach außen. Wie schon bei der Linie, haben die beiden Versionen unterschiedliche Parität.
Doch nun haben wir erst die Hälfte erledigt, denn eine Ebene hat ja zwei Achsen! Als nächstes muß man noch die x-Achse biegen. Aus dem Rohr wird nun ein Torus’ genannt wird (Abb. 11).
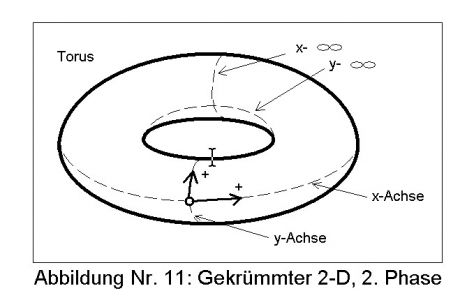
Auch bei diesem Schritt sind zwei Krümmungsrichtungen möglich. In der oben gezeigten Version kommt die Unendlichlinie von y nach innen, im anderen Fall wäre die x-Achse innen gelegen. Insgesamt gibt es also vier Möglichkeiten. Bezeichnet man die Krümmungen mit Minus (-) und Plus (+) so sind die Kombinationen unterschiedlicher Parität : +/+. +/-, -/+ und -/-.
Es gibt noch eine weitere Krümmungsmöglichkeit. Verdreht man eine Seite eines Rechtecks um 180º und verbindet es mit der anderen Seite, so erhält man ein sogenanntes Möbiusband. Die Einhüllende des Möbiusbandes ist ein Torus, den man erhält, wenn man das Band um die x-Achse rotieren läßt.

Die 'Klebestelle' des Rechtecks in Abb. 12 ist die Strecke AB. Wenn man das Möbiusband entlang der Linie x auseinanderschneidet, zerfällt es nicht in zwei Teile, sondern es bleibt eines. Wiederholt man den Vorgang, gibt es zwar zwei Ringe, aber sie sind untrennbar ineinander verflochten. Das läßt sich leicht mit einem Papierstreifen nachvollziehen.
Wenn es zweidimensionale Wesen gäbe, wie könnten sie feststellen, ob sich in ihrem 2-D-Raum Objekte mit mehr als 2 Raumdimensionen befinden? Nehmen wir dazu einmal den Kreis auf der linken Seite von Abb. 13.
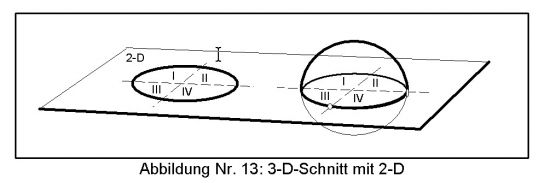
Der Kugelschnitt und der Kreis bilden mit der Ebene die gleiche Figur. Von der 2-D-Ebene aus haben beide Objekte gleiche Form. Nun aber entschließt sich ein 2-D Wesen mit Einsicht in die Dimensionstheorie, den Kreis überkreuz zu zerschneiden. Dann ergeben sich die vier Felder I, II, III und IV, welche nun auseinander gezogen werden können, da sie nicht mehr zusammenhängen.
Das gleiche macht das Wesen nun mit dem anderen Objekt und stellt fest, daß es immer noch ein einziges Objekt geblieben ist, obwohl es wie der Kreis innerhalb des 2-D überkreuz auseinander geschnitten wurde. Die Teile I, II, III und IV lassen sich nicht auseinander ziehen. Aus der Sicht des 3-D wurden in die Kugel nur Löcher gebohrt. Wenn man statt der Kugel einen Torus genommen hätte, wäre der Schnitt mit der Ebene ebenfalls ein Kreis gewesen, mit dem Unterschied, daß er innen ein Loch gehabt hätte.
Ein ähnliches Experiment wie die 2-D-Wesen in ihrem 2-D-Raum können Sie in Ihrem dreidimensionalen Raum ausführen. Nehmen Sie ein Blatt Papier und zeichnen Sie über die Mitte ein Kreuz wie in Abb. 14a. Die eine Linie soll die x-Achse und die andere die y-Achse repräsentieren.
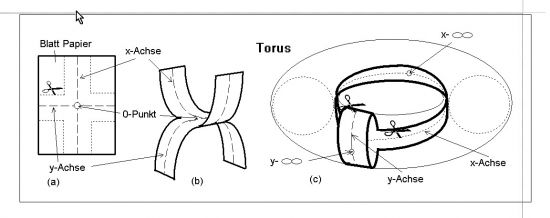
Dann schneiden Sie die Ecken der gepunkteten Linien entlang ab und es entsteht ein Papierkreuz. Nun biegen Sie die gegenüberliegenden Enden wie in Abb. 14b paarweise nach oben und unten und kleben die Enden zusammen. Es entsteht ein Figur wie die in Abb. 14c. Was wir haben, ist ein Teilaspekts eines Torus, der einen gekrümmten 2-D darstellt.
Den gesamten Torus mit planem Papier herzustellen ist zu aufwendig. Die wichtigsten Bestimmungsstücke sind aber bei diesem Modell gegeben. Die Klebestellen entsprechen dem Unendlich von x- und y-Achse. Das vorher aufgezeichnete Kreuz ist immer noch erhalten, nur ist es nun gekrümmt. Jetzt schneiden wir, wie die 2-D-Wesen aus dem vorigen Beispiel, die überkreuz laufenden Achsen mit der Schere auseinander. Das Ergebnis: Obwohl die Linien sich kreuzen, bleibt es 1 Objekt. Und nicht nur das, es hat auch noch exakt die gleiche Größe wie das ursprüngliche Papier.
Die Eigenschaften des Punktes werden in Raumkonstruktionen meist vernachlässigt. Es mag sein, daß sich hier psychologische Wertungen einschleichen, die dem Punkt etwas 'niederes' und 'wertloses' zuschreiben.
Wie wir oben sahen, muß Energie mit sich selbst in Phase sein, um selbst in einem dimensionslosen Feld eine Punktdimension zu konstituieren. 'Phase' ist aber eine Existenzdimension der Punktdimension und kann z.B. geometrisch dargestellt werden. Für eine endlose Existenz dieser Punktdimension 0-D muß der Algorithmus 'Phase' beliebig oft angewendet werden können. Diese Phasenentwicklung kann man als Gerade darstellen, solange man sich bewußt bleibt, daß es keine Raumgerade ist! Das eine Ende dieser Phasengeraden ist der nulldimensionale Raum 0-D. Unter dieser Annahme macht es Sinn zu fragen wie ein gekrümmter 0-D aussieht.
Allgemein wird zur Konstruktion gekrümmter Räume eine zweite Phasenentwicklung angenommen, die von der ersten unabhängig ist, graphisch wird sie also rechtwinklig zur ersten Phase aufgetragen.

Die graphische Darstellung von Abb. 7 soll keinen 3-D-Raum postulieren in dem der Punkt erscheint. Diese visuelle Präsentation der Konstruktion wurde gewählt, weil sie einfacher nachzuvollziehen ist, als der rein algebraische Weg. Die Existenz des Punktes P ist durch die Phasenzyklen der ersten Phasenachse gesichert. Postuliert man eine zweite Phasenachse, so kann man auf ihr die Entwicklung der ersten komprimiert darstellen, was der Krümmung des Punktes in sich selbst entspricht. Der Abstand der Komprimierung ist in Abb. 7 mit r angegeben, auf den Plus-Unendlich projiziert wird und in der anderen Richtung entsprechend die Minuswerte der negativen Zyklen. Der gekrümmte Punkt erscheint als Phasen-Strecke, unterscheidet sich von einer normalen Strecke allerdings durch die Unendlichwerte an den Enden und dem Nullpunkt in der Mitte. Eine normale Strecke auf einer eindimensionalen Geraden ist 'ein Objekt im Raum', wogegen die obige Konstruktion 'einen gekrümmten Raum' herstellt. Dieser Unterschied wird noch mehrfach in den höheren Dimensionen auftauchen. Hier wird auch die Differenz zwischen dem Punkt als 'Dimension' und als 'Objekt' klar. Die Punktdimension braucht keine höheren Strecken-Räume zur Existenz, ein Punktobjekt aber schon.
Der eindimensionale Raum 1-D.
Die Dimension der Linie kann als Objekte Punkte oder Strecken enthalten. In der Regel wird zur Skalierung eine Metrik darauf angewendet, die nach beiden Seiten beliebige Werte annehmen kann. Sieht man eine Gerade nicht nur als Linie an, sondern auch als eindimensionalen Raum, so kann man untersuchen, was bei einer Raumkrümmung des 1-D geschieht; Voraussetzung der Krümmung ist die Einbettung in einen 2-D. In der Mathematik wird oft behauptet, daß die Krümmung auch ohne Einbettung in einen höher dimensionalen Raum gehe. Doch wenn man genau hinschaut was gemacht wird, so erkennt man, daß kein gekrümmter Raum erzeugt wird, sondern ein gekrümmtes Objekt im Raum. Der Unterschied wird im Folgenden deutlich.

Abbildung 8a zeigt die übliche Darstellung des eindimensionalen Raumes (1-D) mit dem Nullpunkt und den beiden Richtungen plus und minus Unendlich, meist nach links und rechts orientiert. Um den 1-D zu krümmen, muß er in einere höhere Dimension eingebettet sein, in den 2-D. Dann kann man 2 Seiten des 1-D feststellen und sie beispielsweise mit plus und minus-Seite benennen. Die plus-Seite wurde in der Abbildung schraffiert, um deutlich zu machen, was bei der Krümmung geschieht. Sie ist auf 2 Weisen möglich, einmal zur plus-Seite hin (b) und einmal nach Minus (c). Der Unendlich-'Punkt' liegt dann irgendwo gegenüber des Nullpunktes, abhängig davon, welche Skalierung man benutzt. Ist sie symmetrisch, liegt Unendlich im 180* Winkel zum Nullpunkt.

Oft wird bei der Darstellung gekrümmter Räume gepfuscht und es wird nicht nur ‘Unendlich’ einfach weggelassen, sondern auch die zweite Krümmung. Dadurch allerdings wird aus der eindimensionalen gekrümmten Dimension ein einfaches gekrümmtes Objekt. Doch es besteht ein fundamentaler Unterschied zwischen
a) gekrümmten Objekten im Raum und
b) gekrümmtem Raum.
Im obigen Beispiel fällt unter a) der Kreis und unter b) der gekrümmte 1-D. Die offensichtlichste Differenz ist die doppelte Existenz des gekrümmten 1-D. Die Darstellungen Abb. 8b und 8c haben unterschiedliche Parität. Geht man in b) vom Nullpunkt aus im Uhrzeigersinn der Linie entlang, bewegt man sich nach minus Unendlich, in c aber nach plus Unendlich! Im Gegenuhrzeigersinn ist es umgekehrt. Ein Kreis dagegen hat keine Parität und alle Punkte auf dem Kreis sind gleichwertig, was im Falle des gekrümmten 1-D nicht der Fall ist.
Angenommen, es gäbe eindimensionale Wesen, wie könnten sie höherdimensionale Objekte erkennen? Als Objekte sind für sie nur Punkte und Strecken erkennbar. Somit würde die Projektion eines Rechtecks parallel zur x-Achse die gleiche Strecke B ergeben, wie die Strecke A in Abb. 9. Doch das ändert sich, wenn das Rechteck gedreht wird. Dann verlängert sich die Strecke und hat innere Endpunkte. Die vorher parallele Seiten erscheinen als C und D. In der Abbildung wurden sie zur Verdeutlichung ein wenig seitlich verschoben. Ein Kreisschnitt mit dem 1-D ergibt zwei Punkte.

Dreht man den Kreis, so bekommen die Schnittpunkte eine zusätzliche Eigenschaft der Gerichtetheit, die zwar nicht direkt im 1-D erkennbar ist, die aber indirekt gewisse Auswirkungen zeigt. Die Ausrichtung der beiden Schnittpunkte ist entweder */* oder */* oder Null/Null. Was nicht möglich ist, sind die Kombinationen */* und */*. Wenn die 1-D-Wesen die Möglichkeit hätten die Ausrichtung zu ändern, dann könnten sie aus ihrer Sicht eine 'Fernwirkung' erfahren. Wenn sie die Richtung der einen Seite von * auf * ändern, wechselt der andere Punkt ebenfalls seine Ausrichtung. Die Verbundenheit der Punkte würde sich auch dadurch zeigen, daß diese Eigenschaft erhalten bleibt, selbst wenn sich die Punkte voneinander entfernen.
Der zweidimensionale Raum 2-D
Um die unterschiedlich verwendeten Begriffe 'Fläche', 'Ebene' und 'Zweidimensionaler Raum' auseinanderzuhalten, treffen wir folgende Konvention: 'Zweidimensionaler Raum' ist der Oberbegriff und umschließt auch nicht-euklidische Konstruktionen. Abgekürzt steht dafür 2-D-Raum, oder wenn es klar ist, daß 'Raum' gemeint ist und nicht 'Zeit', auch nur 2-D. Ein Teilbereich davon sei eine 'Fläche', z.B. eine Oberfläche und wenn sie plan ist, soll sie 'Ebene' heißen.
In Abb. 10a ist ein 2-D mit den beiden Achsen x und y skizziert. Zur Raumkrümmung des 2-D bedarf es einer Einbettung in den 3-D. Man beginnt beispielsweise mit der Krümmung um die y-Achse und erhält die Form einer Röhre (Abb. 10b). Was geschieht dabei mit Unendlich von y? Es kann ja nicht verschwinden, sonst ist es kein gekrümmter 2-D-Raum mehr, sondern nur noch ein gekrümmtes 3-D-Objekt im 3-D-Raum.

Unendlich von y bildet auf der Gegenseite der x-Achse eine Linie. Für die Skalierung der Werte dazwischen bietet sich eine Methode an, die der RIEMANNschen Zahlenkugel verwandt ist. Zieht man von der Unendlich-Linie zur ursprünglichen x/y-Ebene Geraden, so schneiden diese das Rohr an bestimmten Stellen. Auf diese Schnittpunkte werden alle Ebenenpunkte projiziert. In c sind die Punkte A, B, und C als Beispiel gegeben. Bezeichnet man die obere schraffierte Seite der Fläche mit '+', dann kommt in diesem Fall die Plusseite nach innen und die unschraffierte nach außen. Biegt man die Fläche nach unten, so zeigt die schraffierte Fläche nach außen. Wie schon bei der Linie, haben die beiden Versionen unterschiedliche Parität.
Doch nun haben wir erst die Hälfte erledigt, denn eine Ebene hat ja zwei Achsen! Als nächstes muß man noch die x-Achse biegen. Aus dem Rohr wird nun ein Torus’ genannt wird (Abb. 11).

Auch bei diesem Schritt sind zwei Krümmungsrichtungen möglich. In der oben gezeigten Version kommt die Unendlichlinie von y nach innen, im anderen Fall wäre die x-Achse innen gelegen. Insgesamt gibt es also vier Möglichkeiten. Bezeichnet man die Krümmungen mit Minus (-) und Plus (+) so sind die Kombinationen unterschiedlicher Parität : +/+. +/-, -/+ und -/-.
Es gibt noch eine weitere Krümmungsmöglichkeit. Verdreht man eine Seite eines Rechtecks um 180º und verbindet es mit der anderen Seite, so erhält man ein sogenanntes Möbiusband. Die Einhüllende des Möbiusbandes ist ein Torus, den man erhält, wenn man das Band um die x-Achse rotieren läßt.

Die 'Klebestelle' des Rechtecks in Abb. 12 ist die Strecke AB. Wenn man das Möbiusband entlang der Linie x auseinanderschneidet, zerfällt es nicht in zwei Teile, sondern es bleibt eines. Wiederholt man den Vorgang, gibt es zwar zwei Ringe, aber sie sind untrennbar ineinander verflochten. Das läßt sich leicht mit einem Papierstreifen nachvollziehen.
Wenn es zweidimensionale Wesen gäbe, wie könnten sie feststellen, ob sich in ihrem 2-D-Raum Objekte mit mehr als 2 Raumdimensionen befinden? Nehmen wir dazu einmal den Kreis auf der linken Seite von Abb. 13.

Der Kugelschnitt und der Kreis bilden mit der Ebene die gleiche Figur. Von der 2-D-Ebene aus haben beide Objekte gleiche Form. Nun aber entschließt sich ein 2-D Wesen mit Einsicht in die Dimensionstheorie, den Kreis überkreuz zu zerschneiden. Dann ergeben sich die vier Felder I, II, III und IV, welche nun auseinander gezogen werden können, da sie nicht mehr zusammenhängen.
Das gleiche macht das Wesen nun mit dem anderen Objekt und stellt fest, daß es immer noch ein einziges Objekt geblieben ist, obwohl es wie der Kreis innerhalb des 2-D überkreuz auseinander geschnitten wurde. Die Teile I, II, III und IV lassen sich nicht auseinander ziehen. Aus der Sicht des 3-D wurden in die Kugel nur Löcher gebohrt. Wenn man statt der Kugel einen Torus genommen hätte, wäre der Schnitt mit der Ebene ebenfalls ein Kreis gewesen, mit dem Unterschied, daß er innen ein Loch gehabt hätte.
Ein ähnliches Experiment wie die 2-D-Wesen in ihrem 2-D-Raum können Sie in Ihrem dreidimensionalen Raum ausführen. Nehmen Sie ein Blatt Papier und zeichnen Sie über die Mitte ein Kreuz wie in Abb. 14a. Die eine Linie soll die x-Achse und die andere die y-Achse repräsentieren.

Dann schneiden Sie die Ecken der gepunkteten Linien entlang ab und es entsteht ein Papierkreuz. Nun biegen Sie die gegenüberliegenden Enden wie in Abb. 14b paarweise nach oben und unten und kleben die Enden zusammen. Es entsteht ein Figur wie die in Abb. 14c. Was wir haben, ist ein Teilaspekts eines Torus, der einen gekrümmten 2-D darstellt.
Den gesamten Torus mit planem Papier herzustellen ist zu aufwendig. Die wichtigsten Bestimmungsstücke sind aber bei diesem Modell gegeben. Die Klebestellen entsprechen dem Unendlich von x- und y-Achse. Das vorher aufgezeichnete Kreuz ist immer noch erhalten, nur ist es nun gekrümmt. Jetzt schneiden wir, wie die 2-D-Wesen aus dem vorigen Beispiel, die überkreuz laufenden Achsen mit der Schere auseinander. Das Ergebnis: Obwohl die Linien sich kreuzen, bleibt es 1 Objekt. Und nicht nur das, es hat auch noch exakt die gleiche Größe wie das ursprüngliche Papier.
-
Aoife

- Senior Admin

- Beiträge: 7067
- Registriert: 20.09.2008, 21:37
- Wohnort: Ludwigshafen am Rhein
- Ich bin: Keine Angabe
Re: Diskussionspapier: Modell für Zeit und Raum

Klar ist das Recht Nicole, und ich finde deine Arbeit auch durchaus interessantnicole6 hat geschrieben:Meine Sorge hier ist, dass die Arbeit einfach abgelehnt wird, und danach
veröffentlich jemand meine Aussagen unter seinem Namen! Um dem vorzubeugen,
muss ich die Arbeit irgendwo niederlegen, wo man das Datum sehen kann, und wo
es Zeugen gibt, dass die Arbeit an dem Tag deponiert wurde. So kann ich dann
einem eventuellen Plagiatsversuch vorbeugen.
So kam mir die Idee, dass ich die Arbeit hier hochlade, wenn's recht ist.
Deshalb nur um eine Alternative anzudenken, die vielleicht auch interessant sein könnte für dich: Wenn du deine Arbeit als e-book bei Kindle veröffentlichst kostet dich das nichts, und zusätzlich könntest du auch noch ein wenig daran verdienen ... vorausgesetzt dass jemand sie kauft.
Da es sich um eine Orginalarbeit handelt könntest du dich sogar für die höchste Verdienstklasse mit 70% des Listenpreises eintragen, in diesem Fall müsstest du die Beiträge hier allerdings entfernen, da diese Preisklasse voraussetzt dass du Kindle das Alleinvertretungsrecht für die elektronische Version einräumst ... deine Rechte an zusätzlicher physischer Veröffentlichung bleiben hiervon unberührt. Ansonsten bliebe noch die 35% Version für die du weder die alleinigen Rechte am Text benötigst noch du sie auf Kindle überträgst.
Wenn du Kindle-Veröffentlichungen auf dem amazon website aufrufst (beispielsweise meine
Liebe Grüße, Aoife
It's not those who inflict the most, but those who endure the most, who will conquer. MP.Vol.Bobby Sands
'I know kung fu, karate, and 37 other dangerous words'
Misspellings are *very special effects* of me keyboard
'I know kung fu, karate, and 37 other dangerous words'
Misspellings are *very special effects* of me keyboard
-
nicole6

- ModeratorIn

- Beiträge: 2333
- Registriert: 11.09.2009, 13:01
- Wohnort: München
- Ich bin: ehemalige SexarbeiterIn
danke Aoife für den Hinweis!
Aber ich denke, dass so eine Theorie eigentlich nur für
Spezialisten im Physikbereich interessant ist! Ich kann mir
beim besten Willen nicht vorstellen, dass "Normalbürger"
sich damit beschäftigen.
Wie ich schon anfangs schrieb, hatte ich nicht die ganze
Theorie, sondern Teile davon bei Physikkonferenzen
Fachwissenschaftlern der speziellen Bereich vorgestellt,
und bisher konnte mir niemand den kleinsten Fehler
nachweisen! Im Gegenteil, ich konnte jeweils nachweisen,
dass die bisherigen Vorstellungen der akademischen Physik
in sich widersprüchlich sind!
An der Fakultät der Physik in München wollte ich darüber mit
einem der bekanntesten Physikern Deutschlands diskutieren.
Der steigerte sich aber so in Rage und brüllte mich an, was ich
mir als Studentin erlaube die Theorien in Frage zu stellen!
Wenn das so und so in den Büchern stehe, dann sei da so!
Ich verabredete mich dann mit einem anderen Professor.
Der hörte mir zwar zu, sagte aber, dass ich damit wenig
Erfolg haben werde, da die Physiker keinen Bedarf sehen,
eine neue Theorie anzuerkennen, wenn sie nicht auf ihrem
eigenen Mist gewachsen sind!
Ein paar Jahre danach, 1997, las ich einen Artikel in Spektrum
der Wissenschaft, über einen Versuch der Quantenoptik.
So viel ich es auch versuchte, dar gab es einen Punkt darin,
den ich nicht verstand, und ich hatte das Gefühl, dass da an
der Statistik herum gemurkst wurde. So schrieb ich einen der
drei Autoren, Herrn Kwiat an, und er antwortete sogar!
Das interessante an dem Emailwechsel ist, dass ich ihn dazu
brachte, zu schreiben, dass die Mathematik manipuliert wurde!
Anstatt zuzugebem dass die Theorie nicht stimmt, werden
die Gesetze der Mathematik "justiert" !
In der folgenden Mail habe ich den Emailwechsel hochgeladen.
Den "Offenbarumgseid" der Manipulation ist am Ende von mir fett formatiert
Nicole
Aber ich denke, dass so eine Theorie eigentlich nur für
Spezialisten im Physikbereich interessant ist! Ich kann mir
beim besten Willen nicht vorstellen, dass "Normalbürger"
sich damit beschäftigen.
Wie ich schon anfangs schrieb, hatte ich nicht die ganze
Theorie, sondern Teile davon bei Physikkonferenzen
Fachwissenschaftlern der speziellen Bereich vorgestellt,
und bisher konnte mir niemand den kleinsten Fehler
nachweisen! Im Gegenteil, ich konnte jeweils nachweisen,
dass die bisherigen Vorstellungen der akademischen Physik
in sich widersprüchlich sind!
An der Fakultät der Physik in München wollte ich darüber mit
einem der bekanntesten Physikern Deutschlands diskutieren.
Der steigerte sich aber so in Rage und brüllte mich an, was ich
mir als Studentin erlaube die Theorien in Frage zu stellen!
Wenn das so und so in den Büchern stehe, dann sei da so!
Ich verabredete mich dann mit einem anderen Professor.
Der hörte mir zwar zu, sagte aber, dass ich damit wenig
Erfolg haben werde, da die Physiker keinen Bedarf sehen,
eine neue Theorie anzuerkennen, wenn sie nicht auf ihrem
eigenen Mist gewachsen sind!
Ein paar Jahre danach, 1997, las ich einen Artikel in Spektrum
der Wissenschaft, über einen Versuch der Quantenoptik.
So viel ich es auch versuchte, dar gab es einen Punkt darin,
den ich nicht verstand, und ich hatte das Gefühl, dass da an
der Statistik herum gemurkst wurde. So schrieb ich einen der
drei Autoren, Herrn Kwiat an, und er antwortete sogar!
Das interessante an dem Emailwechsel ist, dass ich ihn dazu
brachte, zu schreiben, dass die Mathematik manipuliert wurde!
Anstatt zuzugebem dass die Theorie nicht stimmt, werden
die Gesetze der Mathematik "justiert" !
In der folgenden Mail habe ich den Emailwechsel hochgeladen.
Den "Offenbarumgseid" der Manipulation ist am Ende von mir fett formatiert
Nicole
Zuletzt geändert von nicole6 am 02.03.2014, 21:14, insgesamt 1-mal geändert.
-
nicole6

- ModeratorIn

- Beiträge: 2333
- Registriert: 11.09.2009, 13:01
- Wohnort: München
- Ich bin: ehemalige SexarbeiterIn
RE: Diskussionspapier: Modell für Zeit und Raum
Hier der Emailwechsel mit Herrn Paul G. Kwiat
(http://physics.illinois.edu/people/profile.asp?kwiat)
die interessanteste Aussage ist am Schluss, von mir in fett markiert,
wo er zugibt geschummelt zu haben!
Morgen geht es dann mit dem anderen Artikel weiter.
Nicole
########################################
Dear Mr. P. G. Kwiat
Concerning an experiment published in "Spektrum der
Wissenschaft (Germany), October 1993: " R. Y. CHIAO, P. G.
KWIAT UND AEPHRAIM. M. STEINBERG; 1993; Schneller als
Licht ?; Spektrum d.W. 10/1993;" I have the following question.
As it is explained in the text, before the final experiment was
done, the distances for the two photons had to be adjusted to
have exactly the same length. The photons are created by
spontaneous parametric down-conversion, that means that they
must be absolutely parallel at the start. Because of the
Heisenberg uncertainty law one might not know the exact place,
but as a pair inside the Gauss distribution the two photons are
parallel
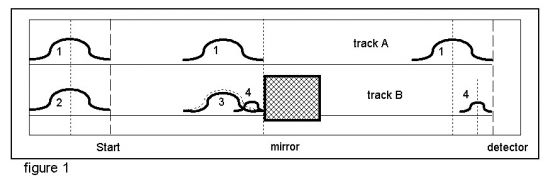
In the text it is written that at the mirror the probability to find
the photons (2) is changing, so the Gauss curve for the
tunneling photon (4) becomes smaller. The bigger part (3) gets
reflected and the maximum of the smaller hump (4) is farther
forward, so it seems that the tunneling photon is faster. (figure
1)
The problem with this explanation is the following:
Sometimes an analogy helps understanding but it can be
misleading too. In this case the Gauss distribution is not
running. For every photon on track A you will find a photon on
track B exactly in the same distance from the start to the
mirror! If the graphic would be correct then the Gauss curve
should be drawn into another (third) dimension forming a three
dimensional tunnel. The length of the tunnel is the distance
between the objects, the height is the point with the heighest
probability to find a photon and the width refers to the
uncertainty gap. So it is clear that there is no movement of the curve.
In the moment photon B arrives at the mirror, photon A is
exactly in the same distance from the start (figure 2). Thus:
both distribution curves have the maximum at the same point!
In the case of tunneling at the entrance of the mirror the
smaller distribution curve must have the maximum exactly at
the same point as photon A. In case there is a measured
difference at the detectors, this cannot be caused by a supposed
shape change of the distribution curve because this would mean
that there is an accumulation of photons on track B with a
distance to the prior maximum with no reference on track A and
no explanation for it. But because of the photon pair production
by spontaneous parametric down-conversion the distribution
on both tracks must be equal between start and mirror.

Now, the experiment shows a difference at the end. For an
explanation, without violating statistical laws and other laws of
nature one can find a solution in changing one basic root
assumption. But in the present moment of scientific politics it is
a heresy because it would suppose a space structure with four
space dimensions instead of three. Then one does not need
any tricks to explain the differences away but the observed
facts would be a necessity.
In case of interest I will write you the basic idea of an
alternative explanation of your experiment.
A copy of this letter is send to
Arthur Jabs, Universidade Federal da Paraiba CCEN , João Pessoa, Brasil
jabs@fisica.ufpb.br
with best regards
A.C.Hofmann
Via Pasina 1, 38066 Riva, Italia
fax: (39) 464 556051
annabella@tecnoprogress.it
__________________________________________________________________________
From: Paul Kwiat[SMTP:kwiat@lanl.gov]
Sent: Mittwoch, 26. November 1997 01:33
To: ABC MAGIC ART; jabs@fisica.ufpb.br
Subject: Re: experiment published 10/1993
Received: from mailhost.lanl.gov (mailhost.lanl.gov
[128.165.3.12]) by tecnop1.tecnoprogress.it (NTMail 3.02.13) with ESMTP id annabella for <annabella>;
Wed, 26 Nov 1997 01:50:37 +0100
Received: from [128.165.51.248] (kwiat.lanl.gov [128.165.51.248])
by mailhost.lanl.gov (8.8.8/(cic-5, 10/28/97)) with ESMTP id RAA08936;
Tue, 25 Nov 1997 17:21:21 -0700 (MST)
X-Sender: kwiat@physics.lanl.gov
Message-Id: <v0311070bb0a0fb8c74e3>
In-Reply-To: <01BCEA47>
Mime-Version: 1.0
Content-Type: text/plain; charset="us-ascii"
Date: Tue, 25 Nov 1997 17:33:31 -0700
To: ABC MAGIC ART <annabella>, jabs@fisica.ufpb.br
From: Paul Kwiat <kwiat>
Subject: Re: experiment published 10/1993
______________________________________________________________________
>Dear Mr. P. G. Kwiat
Hello,
Thank your for your interest in our work. I am afraid, however, that you have a fairly basic incorrect assumption in your
understanding of the phenomenon we describe, as I will point out below.
>As it is explained in the text, before the final experiment was
done, the >distances for the two photons had to be adjusted
to have exacly the same length. The photons are created by
spontaneous parametric down-conversion, that means that
they must be absolutly parallel at the start. Because of the
Heisenberg uncertainty law one might not know the exact place,
but as a pair inside the Gauss distribution the two photons are parallel
But because of the photon pair production by spontaneous
parametric down-conversion the distribution on both tracks
must be equal between start and mirror.
It is not entirely clear by what you mean by "parallel" above,
but it sounds as if you mean that the two photons are
*exactly* the same distance from the crystal, i.e., they
are born at *exactly* the same time. In other words,
they are at precisely the same point under their respective
gaussian probability envelopes. All of your arguments seem
to start with this assumption. This is not a correct statement, however.
The reason is the uncertainty principle. Because each of
the photons has some spread in energy, it also has a small
spread in the time of emission, *relative* to its conjugate
photon (because it is a continuous process, the pair as a
whole has a very very large spread as to when they can be
emitted). But even relatively speaking, there is a spread.
Let me define this "experimentally". Let us assume that we
have infinitely fast detectors, one looking at each of the two
down-conversion directions.
If your conception were correct, than the two detectors would
always fire at *exactly* the same time. This does not happen,
however. Even with perfectly fast detectors, the time between
firings will still give the gaussian distribution. Physically,
the uncertainty principle is the origin of this intrinsic spread:
the photons have a finite bandwidth, which means their
"time" (of origin) cannot be exactly specified. Once one allows
that the photons do not always arrive at exactly the same
time, there is no problem with our description of our experiment, and no need to invoke novel physical theories.
Hope this was comprehensible,
Paul Kwiat
__________________________________________________________
dear Mr. Paul Kwiat,
Thanks for your answer! I appreciate your comments!
Your notes have been very comprehensible, but the arguments
you bring forth do not touch the core of the problem:
the spatial forward shift of the maximum of the gaussian curve.
First the points we both agree:
Inside a certain bandwidth one has the possibility to "find" a
photon. The highest probability is symbolized by the top of the
gauss curve. That means here we have the highest possibility
to find most of the photons. Towards both ends the probability reaches zero.
Because of the uncertainty principle for every single run,
the photons on each track are inside a certain range.
Added together after many thousand runs, the probability
to find a photon on a certain place inside the uncertainty
range is described by the gaussian curve.
Once a photon arrives at the mirror, it might go through or not.
But even if the place of reflection/passing at the mirror is
microscopically stretched out and has to be treated within
the uncertainty principle, statistically the medium of the
place of the maximum number of reflections is fixed.
The problem:
The change of the height of the gauss distribution does not
change the placement of the maximum!
The reason:
The single photons going through the mirror are a selection
of the whole distribution, and not only from the front part of
the curve! The way it is explained in the article will make
one believe that only photons from the first part of the gauss
curve enter the selection to pass the mirror and all the rest
of the curve behind that part has to be reflected. The gauss
curve is the result of the runs of the photons and not vice versa!
As you wrote to me, every photon has a small spread in the
time of emission. The size of this spread is equal for all photons
, and not only for the reflected ones. But that means that all
of the photons passing the mirror take part in the measure
of this spread. So the maximum of the gauss curve becomes
smaller, but the outer limits remain the same. But then it is
not allowed to move the maximum forward! And this is the
real problem I was writing about.
with best regards
A.C.Hofmann
annabella@tecnoprogess.it
________________________________________________________________________________________________________________________
From: Paul Kwiat[SMTP:kwiat@lanl.gov]
Sent: Donnerstag, 27. November 1997 03:02
To: ABC MAGIC ART
Cc: jabs@fisica.ufpb.br
Subject: Re: reply 26.Nov97
Dear Ms. Hofman,
It is good that you seem to understand that intrinsic spread
issues associated with the relative timing of the photons.
Your point, if I understand it correctly, is that there is no
mechanism by which the "back" of the gaussian tale can be
"eaten away" without reducing the rest of the pulse just as
much. In fact, this is exactly what happens in the tunneling
phenomenon, and arises due to the time it takes for the
interference to build up. That is, we can have a tunnel barrier
that basically has destructive interference in the transmitted
direction, which is why most of the incident particles (e.g.
photons) are reflected. However, when a pulse is incident on
the barrier, it takes some time for the coherence to build up (it
is like the time it takes for an optical cavity to "ring down", if
that is any help). During this time (the front of the incident
gaussian), the destructive interference is not so much in effect,
so that any photon in this part of the pulse (although I am
speaking very loosely to ascribe a position to a photon in the
pulse; strictly speaking, we cannot do this) has some higher
probability of being transmitted. After a short time, however,
the coherence is built up, so that basically all of the rest of the
pulse is reflected. In this way, it is possible to have a pulse
reshaping of the sort we describe in the article. The theory for
this has now been worked out at many levels of detail in
many papers, which you might want to look at.
Sincerely,
Paul Kwiat
___________________________________________________________
dear Mr. Paul Kwiat,
first, honestly thanks for spending your time in answering my
questions! It is very difficult to find someone in the scientific
world answering basic questions like this. The reason I mailed
copies to Mr. Arthur Jabs in Brazil is because once he said
starting a lecture in quantum physics at the University of
Munich that one has to be able to ask children's questions,
then one is on the right way to understand physics.
Because of this and his open attitude to problems in
physics I highly esteem Mr. Jabs.
Now to your reply.
To be open, after your last message I am more confused
than before. You are using several terms where the content
is not clear for me.
1.) "pulse" : I know this term used as an energy form
composed by single energy units. For instance "a light pulse"
is composed by single photons as units. The energy of the
single photons taking part in the "pulse" are strictly defined by
the frequency. In case there is only one photon, then there
cannot be any other energy unit "inside" the photon.
2.) "gaussian (distribution)" : I know this term as a statistical term as a (geometrical-numerical) distribution of a theoretically
infinite number of events. One (1) object alone cannot have a gaussian.
You wrote : " ... However, when a pulse is incident on the barrier, ...".
What do you mean by this?
1.) is this a single photon? Obviously not, because then you
write: " ...,so that any photon in this part of the pulse....".
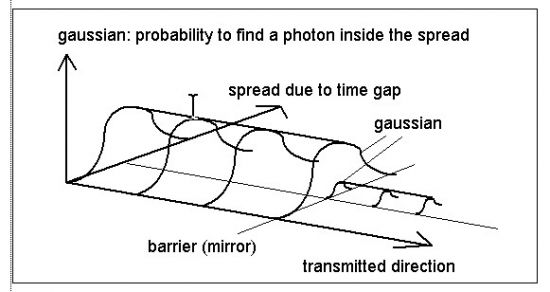
2.) is this the gaussian? The distribution curve does not move either in respect to the transmitted direction.
It is an independent value, occupies an independent dimension
and it has the same value along the track between the
emission point and the barrier and the barrier and detector.
As far as I know, the quantum physics says that absorption
and emission of photons succeed in quantum jumps,
thus the name of the whole part of physics.
If there would not be the jumps, then the absorption lines
could not be so sharp because the only energy parameter of
photons is given by the frequency. "half of a photon" absorbed
"in finite time" cannot exist because it would mean a change
of color due to half of the energy left.
I hope I have been clear where I have the problem in understanding.
You wrote: " ... although I am speaking very loosely to ascribe
a position to a photon in the pulse, strictly speaking, we cannot
do this) ..."
In this way I got the impression that with "pulse" you do not
talk about a single photon nor about the gaussian but a group
of photons. But then, the experiment is about single photons passing a barrier.
Sincerely
Annabella C. Hofmann
________________________________________________________
From: Paul Kwiat[SMTP:kwiat@lanl.gov]
Sent: Montag, 1. Dezember 1997 16:41
To: ABC MAGIC ART
Subject: Re: reply27.Nov97
>dear Mr. Paul Kwiat,
Now to your reply.
To be open, after your last message I am more confused than
before. You are using several terms where the content is not
clear for me.
Sorry to have caused more confusion. It is because I tried to
short-cut the correct but sometimes tedious language.
1.) "pulse" : I know this term used as an energy form composed
by single energy units. For instance "a light pulse" is composed
by single photons as units. The energy of the single photons
taking part in the "pulse" are strictly defined by the frequency.
In case there is only one photon, then there cannot be any
other energy unit "inside" the photon.
By "pulse" I meant "wavepacket", which I hope is more familiar
, and less confusing, to you.
2.) "gaussian (distribution)" : I know this term as a statistical
term as a (geometrical-numerical) distribution of a theoretically
infinite number of events. One (1) object alone cannot have a gaussian.
Well, this is a good topic. I think that in quantum mechanics,
a single photon is in fact described by a probability distribution.
So, for example, I can have a gaussian wavepacket that
describes the probability distribution of a single photon.
You wrote : " ... However, when a pulse is incident on the
barrier, ...". What do you mean by this?
1.) is this a single photon? Obviously not, because then you
write: " ...,so that any photon in this part of the pulse....".
2.) is this the gaussian? The distribution curve does not move
either in respect to the transmitted direction. It is an
independent value, occupies an independent dimension and it
has the same value along the track between the emission point
and the barrier and the barrier and detector.
It is the gaussian wavepacket/wavefunction of a single photon.
It is the probability distribution for an ensemble of such single photons.
You wrote: " ... although I am speaking very loosely to ascribe
a position to a photon in the pulse, strictly speaking, we cannot
do this) ..." In this way I got the impression that with "pulse"
you do not talk about a single photon nor about the gaussian
but a group of photons. But then, the experiment is about single photons passing a barrier.
As above, I am talking about the probability distribution
(or more correctly, the probability amplitude == the
wavefunction) of a single photon. And in fact, this is why
"strictly speaking, we cannot ascribe a position to a photon in
the wavepacket,
because this then means that the wavepacket is *not* the
correct distribution. Nevertheless, I thought it might help you
to think about the problem *as though* the pulse describes
many photons, and some of them sit at the front side, and it is
these that tunnel. But in the orthodox description of QM we
really cannot do this, and one ends up with a superluminal
propagation of the photons. However, this results directly
from the behavior of the gaussian wavepacket undergoing
tunneling, namely, the peak is shifted forward (but the whole
distribution is reduced in amplitude so as to always "fit under"
the unattenuated distribution).
Paul Kwiat
(http://physics.illinois.edu/people/profile.asp?kwiat)
die interessanteste Aussage ist am Schluss, von mir in fett markiert,
wo er zugibt geschummelt zu haben!
Morgen geht es dann mit dem anderen Artikel weiter.
Nicole
########################################
Dear Mr. P. G. Kwiat
Concerning an experiment published in "Spektrum der
Wissenschaft (Germany), October 1993: " R. Y. CHIAO, P. G.
KWIAT UND AEPHRAIM. M. STEINBERG; 1993; Schneller als
Licht ?; Spektrum d.W. 10/1993;" I have the following question.
As it is explained in the text, before the final experiment was
done, the distances for the two photons had to be adjusted to
have exactly the same length. The photons are created by
spontaneous parametric down-conversion, that means that they
must be absolutely parallel at the start. Because of the
Heisenberg uncertainty law one might not know the exact place,
but as a pair inside the Gauss distribution the two photons are
parallel

In the text it is written that at the mirror the probability to find
the photons (2) is changing, so the Gauss curve for the
tunneling photon (4) becomes smaller. The bigger part (3) gets
reflected and the maximum of the smaller hump (4) is farther
forward, so it seems that the tunneling photon is faster. (figure
1)
The problem with this explanation is the following:
Sometimes an analogy helps understanding but it can be
misleading too. In this case the Gauss distribution is not
running. For every photon on track A you will find a photon on
track B exactly in the same distance from the start to the
mirror! If the graphic would be correct then the Gauss curve
should be drawn into another (third) dimension forming a three
dimensional tunnel. The length of the tunnel is the distance
between the objects, the height is the point with the heighest
probability to find a photon and the width refers to the
uncertainty gap. So it is clear that there is no movement of the curve.
In the moment photon B arrives at the mirror, photon A is
exactly in the same distance from the start (figure 2). Thus:
both distribution curves have the maximum at the same point!
In the case of tunneling at the entrance of the mirror the
smaller distribution curve must have the maximum exactly at
the same point as photon A. In case there is a measured
difference at the detectors, this cannot be caused by a supposed
shape change of the distribution curve because this would mean
that there is an accumulation of photons on track B with a
distance to the prior maximum with no reference on track A and
no explanation for it. But because of the photon pair production
by spontaneous parametric down-conversion the distribution
on both tracks must be equal between start and mirror.

Now, the experiment shows a difference at the end. For an
explanation, without violating statistical laws and other laws of
nature one can find a solution in changing one basic root
assumption. But in the present moment of scientific politics it is
a heresy because it would suppose a space structure with four
space dimensions instead of three. Then one does not need
any tricks to explain the differences away but the observed
facts would be a necessity.
In case of interest I will write you the basic idea of an
alternative explanation of your experiment.
A copy of this letter is send to
Arthur Jabs, Universidade Federal da Paraiba CCEN , João Pessoa, Brasil
jabs@fisica.ufpb.br
with best regards
A.C.Hofmann
Via Pasina 1, 38066 Riva, Italia
fax: (39) 464 556051
annabella@tecnoprogress.it
__________________________________________________________________________
From: Paul Kwiat[SMTP:kwiat@lanl.gov]
Sent: Mittwoch, 26. November 1997 01:33
To: ABC MAGIC ART; jabs@fisica.ufpb.br
Subject: Re: experiment published 10/1993
Received: from mailhost.lanl.gov (mailhost.lanl.gov
[128.165.3.12]) by tecnop1.tecnoprogress.it (NTMail 3.02.13) with ESMTP id annabella for <annabella>;
Wed, 26 Nov 1997 01:50:37 +0100
Received: from [128.165.51.248] (kwiat.lanl.gov [128.165.51.248])
by mailhost.lanl.gov (8.8.8/(cic-5, 10/28/97)) with ESMTP id RAA08936;
Tue, 25 Nov 1997 17:21:21 -0700 (MST)
X-Sender: kwiat@physics.lanl.gov
Message-Id: <v0311070bb0a0fb8c74e3>
In-Reply-To: <01BCEA47>
Mime-Version: 1.0
Content-Type: text/plain; charset="us-ascii"
Date: Tue, 25 Nov 1997 17:33:31 -0700
To: ABC MAGIC ART <annabella>, jabs@fisica.ufpb.br
From: Paul Kwiat <kwiat>
Subject: Re: experiment published 10/1993
______________________________________________________________________
>Dear Mr. P. G. Kwiat
Hello,
Thank your for your interest in our work. I am afraid, however, that you have a fairly basic incorrect assumption in your
understanding of the phenomenon we describe, as I will point out below.
>As it is explained in the text, before the final experiment was
done, the >distances for the two photons had to be adjusted
to have exacly the same length. The photons are created by
spontaneous parametric down-conversion, that means that
they must be absolutly parallel at the start. Because of the
Heisenberg uncertainty law one might not know the exact place,
but as a pair inside the Gauss distribution the two photons are parallel
But because of the photon pair production by spontaneous
parametric down-conversion the distribution on both tracks
must be equal between start and mirror.
It is not entirely clear by what you mean by "parallel" above,
but it sounds as if you mean that the two photons are
*exactly* the same distance from the crystal, i.e., they
are born at *exactly* the same time. In other words,
they are at precisely the same point under their respective
gaussian probability envelopes. All of your arguments seem
to start with this assumption. This is not a correct statement, however.
The reason is the uncertainty principle. Because each of
the photons has some spread in energy, it also has a small
spread in the time of emission, *relative* to its conjugate
photon (because it is a continuous process, the pair as a
whole has a very very large spread as to when they can be
emitted). But even relatively speaking, there is a spread.
Let me define this "experimentally". Let us assume that we
have infinitely fast detectors, one looking at each of the two
down-conversion directions.
If your conception were correct, than the two detectors would
always fire at *exactly* the same time. This does not happen,
however. Even with perfectly fast detectors, the time between
firings will still give the gaussian distribution. Physically,
the uncertainty principle is the origin of this intrinsic spread:
the photons have a finite bandwidth, which means their
"time" (of origin) cannot be exactly specified. Once one allows
that the photons do not always arrive at exactly the same
time, there is no problem with our description of our experiment, and no need to invoke novel physical theories.
Hope this was comprehensible,
Paul Kwiat
__________________________________________________________
dear Mr. Paul Kwiat,
Thanks for your answer! I appreciate your comments!
Your notes have been very comprehensible, but the arguments
you bring forth do not touch the core of the problem:
the spatial forward shift of the maximum of the gaussian curve.
First the points we both agree:
Inside a certain bandwidth one has the possibility to "find" a
photon. The highest probability is symbolized by the top of the
gauss curve. That means here we have the highest possibility
to find most of the photons. Towards both ends the probability reaches zero.
Because of the uncertainty principle for every single run,
the photons on each track are inside a certain range.
Added together after many thousand runs, the probability
to find a photon on a certain place inside the uncertainty
range is described by the gaussian curve.
Once a photon arrives at the mirror, it might go through or not.
But even if the place of reflection/passing at the mirror is
microscopically stretched out and has to be treated within
the uncertainty principle, statistically the medium of the
place of the maximum number of reflections is fixed.
The problem:
The change of the height of the gauss distribution does not
change the placement of the maximum!
The reason:
The single photons going through the mirror are a selection
of the whole distribution, and not only from the front part of
the curve! The way it is explained in the article will make
one believe that only photons from the first part of the gauss
curve enter the selection to pass the mirror and all the rest
of the curve behind that part has to be reflected. The gauss
curve is the result of the runs of the photons and not vice versa!
As you wrote to me, every photon has a small spread in the
time of emission. The size of this spread is equal for all photons
, and not only for the reflected ones. But that means that all
of the photons passing the mirror take part in the measure
of this spread. So the maximum of the gauss curve becomes
smaller, but the outer limits remain the same. But then it is
not allowed to move the maximum forward! And this is the
real problem I was writing about.
with best regards
A.C.Hofmann
annabella@tecnoprogess.it
________________________________________________________________________________________________________________________
From: Paul Kwiat[SMTP:kwiat@lanl.gov]
Sent: Donnerstag, 27. November 1997 03:02
To: ABC MAGIC ART
Cc: jabs@fisica.ufpb.br
Subject: Re: reply 26.Nov97
Dear Ms. Hofman,
It is good that you seem to understand that intrinsic spread
issues associated with the relative timing of the photons.
Your point, if I understand it correctly, is that there is no
mechanism by which the "back" of the gaussian tale can be
"eaten away" without reducing the rest of the pulse just as
much. In fact, this is exactly what happens in the tunneling
phenomenon, and arises due to the time it takes for the
interference to build up. That is, we can have a tunnel barrier
that basically has destructive interference in the transmitted
direction, which is why most of the incident particles (e.g.
photons) are reflected. However, when a pulse is incident on
the barrier, it takes some time for the coherence to build up (it
is like the time it takes for an optical cavity to "ring down", if
that is any help). During this time (the front of the incident
gaussian), the destructive interference is not so much in effect,
so that any photon in this part of the pulse (although I am
speaking very loosely to ascribe a position to a photon in the
pulse; strictly speaking, we cannot do this) has some higher
probability of being transmitted. After a short time, however,
the coherence is built up, so that basically all of the rest of the
pulse is reflected. In this way, it is possible to have a pulse
reshaping of the sort we describe in the article. The theory for
this has now been worked out at many levels of detail in
many papers, which you might want to look at.
Sincerely,
Paul Kwiat
___________________________________________________________
dear Mr. Paul Kwiat,
first, honestly thanks for spending your time in answering my
questions! It is very difficult to find someone in the scientific
world answering basic questions like this. The reason I mailed
copies to Mr. Arthur Jabs in Brazil is because once he said
starting a lecture in quantum physics at the University of
Munich that one has to be able to ask children's questions,
then one is on the right way to understand physics.
Because of this and his open attitude to problems in
physics I highly esteem Mr. Jabs.
Now to your reply.
To be open, after your last message I am more confused
than before. You are using several terms where the content
is not clear for me.
1.) "pulse" : I know this term used as an energy form
composed by single energy units. For instance "a light pulse"
is composed by single photons as units. The energy of the
single photons taking part in the "pulse" are strictly defined by
the frequency. In case there is only one photon, then there
cannot be any other energy unit "inside" the photon.
2.) "gaussian (distribution)" : I know this term as a statistical term as a (geometrical-numerical) distribution of a theoretically
infinite number of events. One (1) object alone cannot have a gaussian.
You wrote : " ... However, when a pulse is incident on the barrier, ...".
What do you mean by this?
1.) is this a single photon? Obviously not, because then you
write: " ...,so that any photon in this part of the pulse....".
2.) is this the gaussian? The distribution curve does not move either in respect to the transmitted direction.
It is an independent value, occupies an independent dimension
and it has the same value along the track between the
emission point and the barrier and the barrier and detector.

As far as I know, the quantum physics says that absorption
and emission of photons succeed in quantum jumps,
thus the name of the whole part of physics.
If there would not be the jumps, then the absorption lines
could not be so sharp because the only energy parameter of
photons is given by the frequency. "half of a photon" absorbed
"in finite time" cannot exist because it would mean a change
of color due to half of the energy left.
I hope I have been clear where I have the problem in understanding.
You wrote: " ... although I am speaking very loosely to ascribe
a position to a photon in the pulse, strictly speaking, we cannot
do this) ..."
In this way I got the impression that with "pulse" you do not
talk about a single photon nor about the gaussian but a group
of photons. But then, the experiment is about single photons passing a barrier.
Sincerely
Annabella C. Hofmann
________________________________________________________
From: Paul Kwiat[SMTP:kwiat@lanl.gov]
Sent: Montag, 1. Dezember 1997 16:41
To: ABC MAGIC ART
Subject: Re: reply27.Nov97
>dear Mr. Paul Kwiat,
Now to your reply.
To be open, after your last message I am more confused than
before. You are using several terms where the content is not
clear for me.
Sorry to have caused more confusion. It is because I tried to
short-cut the correct but sometimes tedious language.
1.) "pulse" : I know this term used as an energy form composed
by single energy units. For instance "a light pulse" is composed
by single photons as units. The energy of the single photons
taking part in the "pulse" are strictly defined by the frequency.
In case there is only one photon, then there cannot be any
other energy unit "inside" the photon.
By "pulse" I meant "wavepacket", which I hope is more familiar
, and less confusing, to you.
2.) "gaussian (distribution)" : I know this term as a statistical
term as a (geometrical-numerical) distribution of a theoretically
infinite number of events. One (1) object alone cannot have a gaussian.
Well, this is a good topic. I think that in quantum mechanics,
a single photon is in fact described by a probability distribution.
So, for example, I can have a gaussian wavepacket that
describes the probability distribution of a single photon.
You wrote : " ... However, when a pulse is incident on the
barrier, ...". What do you mean by this?
1.) is this a single photon? Obviously not, because then you
write: " ...,so that any photon in this part of the pulse....".
2.) is this the gaussian? The distribution curve does not move
either in respect to the transmitted direction. It is an
independent value, occupies an independent dimension and it
has the same value along the track between the emission point
and the barrier and the barrier and detector.
It is the gaussian wavepacket/wavefunction of a single photon.
It is the probability distribution for an ensemble of such single photons.
You wrote: " ... although I am speaking very loosely to ascribe
a position to a photon in the pulse, strictly speaking, we cannot
do this) ..." In this way I got the impression that with "pulse"
you do not talk about a single photon nor about the gaussian
but a group of photons. But then, the experiment is about single photons passing a barrier.
As above, I am talking about the probability distribution
(or more correctly, the probability amplitude == the
wavefunction) of a single photon. And in fact, this is why
"strictly speaking, we cannot ascribe a position to a photon in
the wavepacket,
because this then means that the wavepacket is *not* the
correct distribution. Nevertheless, I thought it might help you
to think about the problem *as though* the pulse describes
many photons, and some of them sit at the front side, and it is
these that tunnel. But in the orthodox description of QM we
really cannot do this, and one ends up with a superluminal
propagation of the photons. However, this results directly
from the behavior of the gaussian wavepacket undergoing
tunneling, namely, the peak is shifted forward (but the whole
distribution is reduced in amplitude so as to always "fit under"
the unattenuated distribution).
Paul Kwiat
-
Aoife

- Senior Admin

- Beiträge: 7067
- Registriert: 20.09.2008, 21:37
- Wohnort: Ludwigshafen am Rhein
- Ich bin: Keine Angabe

Hast du schon einmal die physikalische Fakultät der Université de Liège/Belgium als Ansprechpartner in Betracht gezogen?nicole6 hat geschrieben:Ich verabredete mich dann mit einem anderen Professor.
Der hörte mir zwar zu, sagte aber, dass ich damit wenig
Erfolg haben werde, da die Physiker keinen Bedarf sehen,
eine neue Theorie anzuerkennen, wenn sie nicht auf ihrem
eigenen Mist gewachsen sind!
Wer Haramein's Berechnungen zum Schwarzschildproton für preiswürdig erachtet kann IMHO nicht ganz so engstirnig sein
Liebe Grüße, Aoife
It's not those who inflict the most, but those who endure the most, who will conquer. MP.Vol.Bobby Sands
'I know kung fu, karate, and 37 other dangerous words'
Misspellings are *very special effects* of me keyboard
'I know kung fu, karate, and 37 other dangerous words'
Misspellings are *very special effects* of me keyboard
-
nicole6

- ModeratorIn

- Beiträge: 2333
- Registriert: 11.09.2009, 13:01
- Wohnort: München
- Ich bin: ehemalige SexarbeiterIn
wie schon gesagt, bzw. geschrieben, versuchte ich es an der
Fakultät Physik in München, wo ich studierte.
Ich war meist bei Professor Arthur Jabs, von der Universidade
Federal da Paraiba CCEN , João Pessoa, Brasil, der damals
in München eine Gastprofesssur hatte. Der war eigentlich offen.
Aber leider nicht konsequent. Ich wies ihn darauf hin, dass die
Theorie zum Brechungsgesetz falsch sei. Dort wird behauptet,
dass Licht im Prisma aufgespalten wird, aber an planem Glas nicht.
Woher soll aber das Licht beim Eintritt wissen, welchen
Winkel die andere Seite hat?
Jabs meinte, dass die Brechunm immer stattfinde, aber bei
planem Glas so winzig sei, dass man es nicht sehe.
Dann berechnet ich ihm für 1cm dickes Glas die angebliche Aufspaltung,
und legte ihm die Rechnung vor. Er schaute sie an, runzelte die Stirn,
und meinte, tja, das ist ja interessant !
Das wars dann.
Nicole
Fakultät Physik in München, wo ich studierte.
Ich war meist bei Professor Arthur Jabs, von der Universidade
Federal da Paraiba CCEN , João Pessoa, Brasil, der damals
in München eine Gastprofesssur hatte. Der war eigentlich offen.
Aber leider nicht konsequent. Ich wies ihn darauf hin, dass die
Theorie zum Brechungsgesetz falsch sei. Dort wird behauptet,
dass Licht im Prisma aufgespalten wird, aber an planem Glas nicht.
Woher soll aber das Licht beim Eintritt wissen, welchen
Winkel die andere Seite hat?
Jabs meinte, dass die Brechunm immer stattfinde, aber bei
planem Glas so winzig sei, dass man es nicht sehe.
Dann berechnet ich ihm für 1cm dickes Glas die angebliche Aufspaltung,
und legte ihm die Rechnung vor. Er schaute sie an, runzelte die Stirn,
und meinte, tja, das ist ja interessant !
Das wars dann.
Nicole
-
nicole6

- ModeratorIn

- Beiträge: 2333
- Registriert: 11.09.2009, 13:01
- Wohnort: München
- Ich bin: ehemalige SexarbeiterIn
RE: Diskussionspapier: Modell für Zeit und Raum
FORTSETZUNG DER THEORIE
################################
Den gesamten Torus mit planem Papier herzustellen ist zu aufwendig. Die wichtigsten Bestimmungsstücke sind aber bei diesem Modell gegeben. Die Klebestellen entsprechen dem Unendlich von x- und y-Achse. Das vorher aufgezeichnete Kreuz ist immer noch erhalten, nur ist es nun gekrümmt. Jetzt schneiden wir, wie die 2-D-Wesen aus dem vorigen Beispiel, die überkreuz laufenden Achsen mit der Schere auseinander. Das Ergebnis: Obwohl die Linien sich kreuzen, bleibt es 1 Objekt. Und nicht nur das, es hat auch noch exakt die gleiche Größe wie das ursprüngliche Papier.
Was geschieht nun, wenn ein Torus den 2-D schneidet? In Abb. 15 ergibt der vertikale Schnitt eines Torus mit einer Ebene zwei Kreise. Von der Ebene aus gesehen, unterscheidet sich dieser Schnitt nicht von einem Kreis, außer, wenn sich der Torus dreht. Dann bekommen die 'Kreise' Eigenschaften, die normale Kreise nicht haben. Vor allem ist offensichtlich, daß diese Eigenheiten, wenn man sie mit einem Pfeil kennzeichnet, paarweise entgegengesetzt sind. Wenn der eine Pfeil nach 'oben' zeigt, ist der anderen nach unten gerichtet. Diese Orientierung ist natürlich im 2-D nur indirekt feststellbar. Eine weitere Version der Orientierung des Torus zum 2-D ist in Abb. 16 gegeben.
Vom 2-D aus bildet nun der Schnitt des Torus einen Kreis und nicht zwei, wie vorher, obwohl es das selbe Objekt ist. Die Kombinationsmöglichkeiten der Drehbewegungen wurden schon im Abschnitt der Raumkonstruktion mit 9 Dimensionen angegeben. Hier möchte ich noch eine Variation präsentieren, die in der Atomphysik eine Rolle spielt. Bis heute werden die Elementarteilchen als kugelförmig angesehen, und da ist es unmöglich sich ein Objekt vorzustellen, welches 'sich zweimal drehen muß, um eine volle Drehung zu vollziehen'. Das klingt paradox, ist es aber nicht, da diese Bewegung mit einem Torus möglich ist. Eine 'volle Drehung' eines Objekts ist gegeben, wenn alle Punkte des Objekts vorher und nachher wieder am gleichen Ort sind.
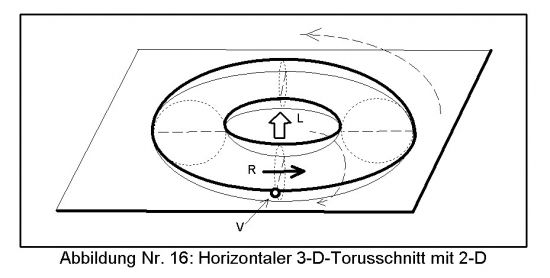
Jetzt stellt man sich den Torus als Fahrradschlauch vor, bei dem die beiden Drehungen um die Achsen R und L im Verhältnis 1 zu 2 stehen. Beginnt man mit dem Ventil V außen, so hat sich nach einer vollen 360º Drehung um L das Ventil V um 180º gedreht und zeigt nach innen. Erst nach der zweiten Drehung zeigt das Ventil wieder nach außen und alle Punkte sind wieder an ihrem vorigen Ort. Vom 2-D aus ist allerdings dieser innere Drehvorgang nicht ersichtlich. Ein Beobachter im 2-D kann nur die 360º Drehung um die L-Achse erkennen. Diese Eigenschaft wird in der Physik 'Spin' genannt.
Der dreidimensionale Raum 3-D
Zur Darstellung der Krümmung eines 3-D braucht man im Prinzip vier Dimensionen. Die Krümmungen um zwei Achsen ergeben schon einen räumlichen Torus, wie ich im vorigen Abschnitt zeigte. Reduziert man diesen Torus um eine Dimension und projiziert ihn auf eine Ebene, bleibt ein Kreisring übrig (Abb. 17).
Die dritte Dimension steht nun senkrecht auf dieser x-y-Projektion. Um die volle 3-D Krümmung zu erreichen, muß man die Torusprojektion um die z-Achse krümmen und man erhält einen Hypertorus. Zu berücksichtigen ist, daß auch die Abb. 17 nur einen Aspekt des Hypertorus darstellen kann. Bezeichnet man die Krümmungsrichtungen wie bei der Ebene mit '+' und '-' , so erhält man folgende 8 Kombinationen: +/+/+, +/+/-, +/-/-, -/-/-, -/-/+, -/+/+, +/-/+ und -/+/-. Wichtig ist dabei, daß diese Variationen keine Alternativen des gekrümmten 3-D darstellen, sondern integrative Teilaspekte sind!
Alle acht Kombinationen zusammen bilden erst den gekrümmten 3-D! In der Literatur wird manchmal darüber diskutiert, ob der gekrümmte 3-D Sattelform habe oder sphärisch ist. Das hängt vom Standpunkt des Beobachters ab. Vom inneren Torusloch aus gesehen, erscheint die Oberfläche als Sattel, von außen ist die Krümmung gleichgerichtet und erscheint mit sphärischen Charakter.
Die Codimension
Normalerweise braucht man zur mathematischen Darstellung eines mehrdimensionale Raumes soviel Gleichungen wie es Dimensionen gibt, d.h. für einen Raum mit 100 Dimensionen benötigt man ebenso viele Gleichungen. Doch betrachtet man ein Objekt in diesem Raum, so braucht man zur mathematischen Darstellung nur so viele Gleichungen, wie es der Differenz zwischen der Dimension des Objekts und des Einbettungsraums entspricht. Hat die Einbettung 100 und das Objekt 99 Dimensionen, so braucht man nur 1 Gleichung. Man spricht auch von Codimension. Objekte mit gleicher Codimension haben ähnliche Eigenschaften Ein 1-D-Punkt teilt eine 2-D-Gerade in zwei Stücke, eine 2-D-Ebene teilt einen 3-D-Raum in zwei Hälften und ein Objekt der Codimension 1 teilt einen 33-dimensionalen Raum in zwei Stücke. Die Zweiteilung findet auch statt, wenn man innerhalb einer Dimension diejenige krümmt, die um 1 kleiner ist, wie es in Abb. 18 skizziert ist.
Zum leichteren Verständnis wurde in die gekrümmte Ebene eine dick ausgezogene Hilfslinie eingezeichnet, aus der man erkennt, daß man hier einen ins Unendliche ausgestreckten MÖBIUSring vor sich hat. Die Codimension ist besonders interessant, wenn man nicht so genau weis, wieviel Elemente überhaupt in einer Sache beteiligt sind und die vielleicht sogar wechseln, wobei es dann zu einer unscharfen Menge kommt. Im Allgemeinen bleibt die Eigenschaft der Codimension erhalten, selbst wenn man die 'überflüssigen' Dimensionen wegstreicht. Dies gibt uns die Berechtigung, bei Betrachtung eines höherdimensionalen Objekts, z.B. eines 4-D-Torus im Schnitt mit dem 3-D die topologischen Eigenschaften eines 3-D-Torus zugrunde zu legen. Ein Beispiel in einsehbare Dimensionen ist der Schnitt eines 3-D-Kugel mit einer 2-D-Fläche. Die Codimension ist 3-2=1, d.h. der Schnitt läßt sich durch 1 Gleichung darstellen, obwohl es ein zweidimensionales Objekt ist, nämlich ein Kreis mit der Gleichung U=2r(pi).
9. NICHT-EUKLIDISCHE RÄUME
Als Konsequenz der allgemeinen Relativitätstheorie gibt es keinen starren Körper innerhalb Gravitationsfelder. Während ihrer Bewegung werden die Körper beliebigen Gestaltsänderungen unterzogen, wenn sie sich an anderen Massen vorbeibewegen. Zur Bestimmung der Veränderungen benutzt man das Modell eines nichtstarren Bezugskörpers, " den man nicht mit Unrecht als "Bezugsmolluske" bezeichnen könnte" .
HANS REICHENBACH zeigt in seinem Buch 'Philosophie der Raum-Zeit-Lehre' mit einer Zeichnung, wie, von einem höheren Einbettungsraum aus gesehen, ein Beobachter in einem gekrümmten Raum den Horizont sieht (Abb. 19).
REICHENBACH unterstellt eine sphärische Kugel, obwohl ein gekrümmter Raum torusartig ist. Aber da die Projektion eines Torus auf eine Ebene der einer Kugel gleicht, kann man die Überlegung prinzipiell beibehalten. Um die Konsequenzen zu verallgemeinern, muß man sie allerdings für alle drei Richtungen im 3-D anwenden. In Abb. 19 schaut ein Beobachter von A aus zum Horizont. Die 'Gerade', die ein Lichtstrahl dabei entlangläuft, entspricht der gepunkteten Linie. Wichtig ist der Umstand, daß es auf der anderen Seite des gekrümmten Raumes einen 'Schattenraum' gibt, der für den Beobachter von A aus prinzipiell uneinsehbar ist, ein Umstand, der bisher von den Astronomen in ihren Überlegungen des gekrümmten Universums kaum beachtet wurde!
10. SPIEGELKUGEL-MODELL
Am einfachsten wäre die übliche Reduzierung einer Dimension des 3-D auf eine Ebene, die im Folgenden mit 2-D abkürzen wird, unabhängig davon ob sie plan oder gekrümmt ist.
Aber hier interessiert, was simultan außerhalb und innerhalb eines 3-D geschehen kann, und wie sich 4-D-Ereignisse im 3-D manifestieren können. Dazu benötigt man aber eine räumliche Darstellung des 3-D-Raums innerhalb eines 4-D-Raums. Mit gewissen Einschränkungen sind dazu folgende Modelle brauchbar. Stellt man sich eine verchromte Stahlkugel vor (Abb. 20.), so spiegelt sich auf ihr der gesamte sphärische Raum. Die Abbildung ist zwar verzerrt, aber wenn man auf ihr sehr kleine Flächenstücke herausgreift, kann man die Abweichungen vernachlässigen.
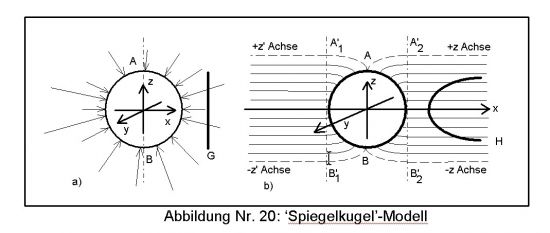
Nun belassen wir die Projektionspunkte auf der Kugel und biegen die Halbschalen nach außen, bis sie zur vorigen Richtung der z-Achse parallel sind. Eine Linie die vorher eine Gerade (G) war, wird dann zur Kurve H in Abb. 20b. Der positive und negative Ast der z-Achse spaltet sich in eine z- und z'-Achse auf . Der Vorteil dieser Version ist, daß man den 3-D mit einer gewissen 'Dicke' darstellen kann und innerhalb der 3-D-Darstellung auch noch die vierte Platz hat.
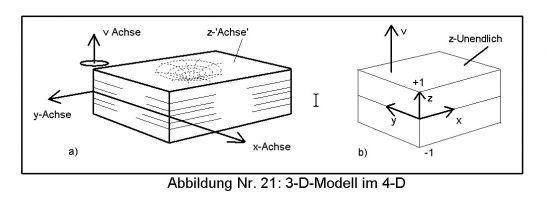
Die vierte Dimension muß definitionsgemäß auf allen anderen senkrecht stehen, was mit Ausnahme des Trichters überall gegeben ist. In Abb. 21a ist ein Stück dieses Raummodells wiedergegeben. Die z-Achse bildet nun die Deck-'Fläche' des Raumstücks.
Eine Variation des Modells von a ist in b gegeben. Hier wurde die z-Dimension gewissermaßen von Unendlich auf den Wert 1 zusammengequetscht . Der Zahl '+1' entspricht dabei plus Unendlich und '-1' steht für minus Unendlich von z. Der positive Wert der Z-Achse zeigt dabei immer noch nach oben und ist damit parallel zur Darstellung der vierten Dimension v. In dieser Version sind bei Untersuchungen der vierten Dimension nur Eigenschaften der x-y-Ebene in Bezug auf v gültig, ansonsten kann die z-Achse hinzugezogen werden.
Gesetzt der Fall, es gäbe zweidimensionale Wesen, könnten sie auf direktem Wege eine transversale Schwingung einer Ebene nicht wahrnehmen, da die Schwingungsrichtung nicht innerer Teil ihres Systems ist. Für sie sind nur Longitudinalschwingungen direkt erfahrbar. Allerdings gibt es im Falle einer permanenten Transversalschwingung eine besondere Erscheinung in der 2-D-Welt. Die 2-D-Wesen werden entdecken, daß es für sie eine Grenzgeschwindigkeit gibt, die von der Länge des Objektes abhängt. Wenn die Wellenlänge im Vergleich zum Objekt sehr groß ist, werden sie eine Grenzgeschwindigkeit postulieren, die nicht überschreitbar ist. Es ist die Fortpflanzungsgeschwindigkeit der Transversalwelle der Ebene. Im 3-D entspricht dies dem Rumpfwiderstand von Segelbooten im Wasser.
Geht man vom 2-D zum 3-D so gibt es bei einer Einbettung in den 4-D noch eine dritte Schwingungsart. Hier erfolgt die Auslenkung der gesamten 3-D-Raummatrix in Richtung des 4-D, im folgenden 'Matrix-Schwingung genannt (Abb. 23).

Wie schon im Beispiel des 2-D ist auch hier vom 3-D aus auf direkte Weise dieser Schwingungszustand nicht erkennbar; allerdings indirekt, wie schon im vorigen Beispiel. Der Energietransport auf der Basis der Matrixschwingung erfolgt zwar innerhalb des 3-D, aber die Auslenkung nimmt einen Verlauf, der zu allen drei Dimension senkrecht steht. Dabei können im 3-D getrennte Orte verbunden werden, welche im 4-D einen einzigen Energieträger darstellen, beispielsweise in Torusform. Die Matrixschwingung wirkt auch innerhalb der 3-D-Objekte, da das 'Innere' eines Gegenstandes vom 4-D aus offen daliegt, so wie man vom 3-D aus das 'Innere' eines Kreises sehen kann und vom 2-D aus das 'Innere' einer Strecke.
11. DIE FRAKTALE DIMENSION 1.37
Ein interessantes Ergebnis ergaben 1986 Versuche von K. R. SREENIVASAN und C. MENEVAU über die fraktale Dimension von turbulenten Jetströmungen, die von ruhiger Flüssigkeit umgeben sind. Sie kamen auf einen Wert von 1.37 für Turbulenzen auf Ebenen. Diese Ziffernfolge ist Physikern bekannt. "Es war Richard Feynman, in der Tat, der anregte, daß alle Physiker in ihrem Office oder Heim ein Schild aufstellen, um sie daran zu erinnern, wie wenig sie wissen. Auf diesem Schild wäre nur dieses: 137". Diese Ziffernfolge bezieht sich auf die sogenannte ‘Feinstrukturkonstante Alpha’ (*). "Diese Konstante wurde ursprünglich von dem deutschen Physiker Arnold Sommerfeld zu Beginn eingeführt; sie ist eine reine Zahl und muß im Experiment gemessen werden" . Bei Nuklearteilchen ist nicht die gesamte Energie zu Masse verdichtet, 1/137 davon bleibt frei. Es ist die Stärke der elektromagnetischen Wechselwirkung. "Sie ist der Quotient aus dem Quadrat der elektrischen Ladung eines Elektrons und dem Produkt aus Lichtgeschwindigkeit und der Planckschen Konstanten der Quantentheorie ... Wir wissen nicht, warum diese beiden Zahlen genau diese Werte haben. Wären sie anders, wäre auch unser gesamtes Universum anders, vielleicht sogar unvorstellbar anders."
Nun kann es natürlich Zufall sein, daß sich die beiden Werte gleichen. Doch wie ich weiter unten noch zeigen werde, gibt es handfeste Hinweise, daß die Feinstrukturkonstante * mit hoher Wahrscheinlichkeit einen torusförmigen Aufbau der Atome aus Quarks beschreibt. Mit den von K. R. SREENIVASAN und C. MENEVAU durchgeführten Experimenten über turbulente Strahlen beschäftigten sich nämlich schon J. J. THOMSON und H. F. NEWALL. Im Jahr 1885 veröffentlichten sie einen Bericht mit dem Titel "On the Formation of Vortex-Rings by Drops" und 1918 beschrieb EMIL HATSCHEK seine Experimente mit Gelatine, wo er den Nachweise der großen Empfindlichkeit der Formenbildung führte, die von der Dichte der Flüssigkeit bis zur dritten Stelle nach dem Komma abhing . 1877 veröffentlichte A.OVERBECK in "Wiedemanns Analen II" seine Untersuchungsergebnisse von Wirbelbildung in Flüssigkeiten. Allen diesen Forschungen ist ein Ergebnis gemeinsam: Die Wirbelbildung der Strömungen in ruhiger Umgebung erfolgt in Torusform! Daß * die Ziffernfolge 137 hat und nicht 237, wie es für eine dreidimensionale Strömung nötig wäre, könnte ein Hinweis darauf sein, daß diese Dynamik eine geschlossene Kurve auf der Torusform beschreibt, worauf auch der glatte Wert des Spin 1/2 hinweist.
Es gibt noch eine Verbindung zwischen dem Spin 1/2 und der Torusform, die von WHEELER gezeigt wurde. Er erklärt den Zusammenhang anhand eines Würfels, dessen Ecken mittels elastischer Schnüre an Raumecken befestigt sind. Als Modell dafür dient die Projektion eines 4-D-Würfels. Hier kann man einen Würfel als Zimmer ansehen und den anderen Würfel als den zu drehenden. Verbindungsschnüre seien als dünne Linien gegeben.
Dreht man nun den Würfel um eine der drei Mittelachsen um 360°, dann nimmt er zwar wieder die ursprünglliche Lage an, aber die Schnüre sind verdrillt. Erst eine weitere Drehung um nochmals 360°, insgesamt sind es nun 720°, entwirrt die Schnüre wieder. Damit das nicht allzu theoretisch wird, fordert WHEELER uns zu einem 'handgreiflichen' Experiment mit einem Gürtel auf: "Man nehme einen Gürtel und lege ihn flach ausgestreckt auf einen Tisch. Das eine Ende fixiere man, während man das andere Ende um 720° dreht. Nun schiebt man das verdrehte Ende unter Beibehaltung der Orientierung um das andere Ende herum und - der Gürtel ist wieder ausgedreht. Bei einer 360°-Verdrehung ist das nicht so. Der Gürtel steht mit dem Würfel, dem Zimmer und den acht elastischen Schnüren in Beziehung. Bevor man den Würfel überhaupt dreht, kann man ihn aus einem Fenster ziehen. In einiger Entfernung nehmen dann die acht elastischen Schnüre die Form eines Gürtels an."
12. BEISPIEL FÜR FRAKTALE: ELEKTRONENHÜLLE
In den folgenden Kapiteln werde ich noch zeigen, daß es Sinn macht, bei Elektronen die topologische Form eines rotierenden vierdimensionalen Torus anzunehmen, weil damit viele Eigenschaften erklärt werden können, die sonst unbeantwortet bleiben. In der hier vorgeschlagenen Dynamik entsteht eine Asymmetrie in der Kopplung zweier Elektronen. Ein Elektron als dynamischer Torus (Abb. 24) mit Spin 'up' (*) kann wegen der Richtung des Energieflusses ein anderes Elektron auf der ‘Unterseite’ nur innen bei der Zentralachse, auf der ‘Oberseite’ nur außen am Torusumfang ankoppeln, d.h. das andere muß Spin 'down' (*) haben. Dann bilden beide Elektronen zusammen einen geschlossenen Torusring der sich nach innen dreht. Die Kombinationen ** oder ** sind dynamisch nicht möglich.
Ein 4-D-Torus erscheint im Schnitt mit dem 3-D-Raum als Sphäre. Im rechten Teil der Abb. 24 soll somit ein 4-D-Elektronentorus durch eine 3-D-Sphäre symbolisiert werden. In einem Atom ist die erste Elektronenschale (K) mit einem 'up'- und einem 'down'-Elektron abgesättigt. Man findet hier also 2 Elektronen. Das nächste stabile Muster ist durch eine Tetraederform gegeben. Hier sind 4 Sphären zu einer kompakten Figur zusammengefügt. In die Lücken der Vierergruppe passen nochmals vier Sphären in der Orientierung eines umgedrehten Tetraeders und wir sind bei 8 Elektronen angelangt, welche die zweite (L-) Schale abschließen.
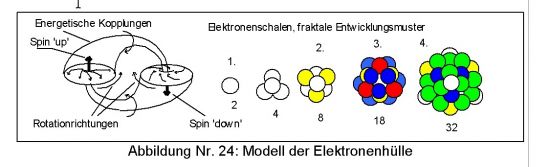
Die weiteren Anordnungen sind in Abb. 24 zu skizzieren, es erleichtert aber erheblich das Verständnis, wenn man die Modelle mit richtigen Kugeln konstruiert. Verschiedenfarbige billige Plastikkugeln, die es in jedem Spielzeugladen gibt, reichen dazu völlig aus. Zum Zusammenkleben eignet sich eine Heißklebepistole.
Ist beispielsweise die L-Schale mit 4 weißen und 4 gelben Kugeln zusammengeklebt, so nimmt man für die 18 Elektronen der M-Schale 6 rote und 12 blaue Kugeln. Nun passen zwischen die gelben Kugeln genau 6 rote und anschließend zwischen die roten 12 blaue Kugeln (Abb. 24, 3. Schale). Die blauen Kugeln bilden nun mit jeweils 4 Dreiergruppen die erste fraktale Untergliederung über dem Tetraeder aus den primären weißen Kugeln, bzw. Elektronen.
Mit der N-Schale, die 32 Elektronen hat, geht es ähnlich. 24 grüne Kugeln passen so in die Lücken des Vorläufers, dass am Ende 4 gelbe und 4 weisse Kugeln genau über den Positionen im Kern der 8er-L-Schale zu liegen kommen.
Man sieht hier, dass sich im räumlich-sphärischen 3-D Aufbau der Elektronenhülle, mit den Vorgaben der Quantisierung und dem Aufsuchen des minimalen Energielevels, eine fraktale Entwicklung entfaltet, die aus ineinandergeschachtelten Tetraedern zusammengesetzt ist.
Nun soll das Beispiel nicht dazu verleiten, sich die Elektronen als feste Teilchen vorzustellen. Aber auch wenn man den Wellencharakter berücksichtigt, ist das obige Beispiel anwendbar. Dann stehen die Kugeln für Resonanzknoten der Wellenmuster in der Topologie der Energieverteilung. Mit diesem Modell der Topologie der Elektronenhülle läßt sich auch erklären, warum die Edelgase Neon bis Radon keine Verbindungen mit anderen Elementen eingehen. Ein Elektron mit Spin 'up' und eines mit Spin 'down' bilden jeweils ein Paar. Vier solche Paare bilden ein Tetraeder, welches aus vier gleichseitigen Dreiecken besteht. Durch die gleichen Abstände der Ecken kann die Struktur in Resonanzschwingung geraten, welche eventuelle Verbindungen mit anderen Atomen abreißen lässt. Im Heliumatom bilden die 2 Protonen und 2 Neutronen einen Tetraeder.
################################
Den gesamten Torus mit planem Papier herzustellen ist zu aufwendig. Die wichtigsten Bestimmungsstücke sind aber bei diesem Modell gegeben. Die Klebestellen entsprechen dem Unendlich von x- und y-Achse. Das vorher aufgezeichnete Kreuz ist immer noch erhalten, nur ist es nun gekrümmt. Jetzt schneiden wir, wie die 2-D-Wesen aus dem vorigen Beispiel, die überkreuz laufenden Achsen mit der Schere auseinander. Das Ergebnis: Obwohl die Linien sich kreuzen, bleibt es 1 Objekt. Und nicht nur das, es hat auch noch exakt die gleiche Größe wie das ursprüngliche Papier.
Was geschieht nun, wenn ein Torus den 2-D schneidet? In Abb. 15 ergibt der vertikale Schnitt eines Torus mit einer Ebene zwei Kreise. Von der Ebene aus gesehen, unterscheidet sich dieser Schnitt nicht von einem Kreis, außer, wenn sich der Torus dreht. Dann bekommen die 'Kreise' Eigenschaften, die normale Kreise nicht haben. Vor allem ist offensichtlich, daß diese Eigenheiten, wenn man sie mit einem Pfeil kennzeichnet, paarweise entgegengesetzt sind. Wenn der eine Pfeil nach 'oben' zeigt, ist der anderen nach unten gerichtet. Diese Orientierung ist natürlich im 2-D nur indirekt feststellbar. Eine weitere Version der Orientierung des Torus zum 2-D ist in Abb. 16 gegeben.

Vom 2-D aus bildet nun der Schnitt des Torus einen Kreis und nicht zwei, wie vorher, obwohl es das selbe Objekt ist. Die Kombinationsmöglichkeiten der Drehbewegungen wurden schon im Abschnitt der Raumkonstruktion mit 9 Dimensionen angegeben. Hier möchte ich noch eine Variation präsentieren, die in der Atomphysik eine Rolle spielt. Bis heute werden die Elementarteilchen als kugelförmig angesehen, und da ist es unmöglich sich ein Objekt vorzustellen, welches 'sich zweimal drehen muß, um eine volle Drehung zu vollziehen'. Das klingt paradox, ist es aber nicht, da diese Bewegung mit einem Torus möglich ist. Eine 'volle Drehung' eines Objekts ist gegeben, wenn alle Punkte des Objekts vorher und nachher wieder am gleichen Ort sind.

Jetzt stellt man sich den Torus als Fahrradschlauch vor, bei dem die beiden Drehungen um die Achsen R und L im Verhältnis 1 zu 2 stehen. Beginnt man mit dem Ventil V außen, so hat sich nach einer vollen 360º Drehung um L das Ventil V um 180º gedreht und zeigt nach innen. Erst nach der zweiten Drehung zeigt das Ventil wieder nach außen und alle Punkte sind wieder an ihrem vorigen Ort. Vom 2-D aus ist allerdings dieser innere Drehvorgang nicht ersichtlich. Ein Beobachter im 2-D kann nur die 360º Drehung um die L-Achse erkennen. Diese Eigenschaft wird in der Physik 'Spin' genannt.
Der dreidimensionale Raum 3-D
Zur Darstellung der Krümmung eines 3-D braucht man im Prinzip vier Dimensionen. Die Krümmungen um zwei Achsen ergeben schon einen räumlichen Torus, wie ich im vorigen Abschnitt zeigte. Reduziert man diesen Torus um eine Dimension und projiziert ihn auf eine Ebene, bleibt ein Kreisring übrig (Abb. 17).
Die dritte Dimension steht nun senkrecht auf dieser x-y-Projektion. Um die volle 3-D Krümmung zu erreichen, muß man die Torusprojektion um die z-Achse krümmen und man erhält einen Hypertorus. Zu berücksichtigen ist, daß auch die Abb. 17 nur einen Aspekt des Hypertorus darstellen kann. Bezeichnet man die Krümmungsrichtungen wie bei der Ebene mit '+' und '-' , so erhält man folgende 8 Kombinationen: +/+/+, +/+/-, +/-/-, -/-/-, -/-/+, -/+/+, +/-/+ und -/+/-. Wichtig ist dabei, daß diese Variationen keine Alternativen des gekrümmten 3-D darstellen, sondern integrative Teilaspekte sind!

Alle acht Kombinationen zusammen bilden erst den gekrümmten 3-D! In der Literatur wird manchmal darüber diskutiert, ob der gekrümmte 3-D Sattelform habe oder sphärisch ist. Das hängt vom Standpunkt des Beobachters ab. Vom inneren Torusloch aus gesehen, erscheint die Oberfläche als Sattel, von außen ist die Krümmung gleichgerichtet und erscheint mit sphärischen Charakter.
Die Codimension
Normalerweise braucht man zur mathematischen Darstellung eines mehrdimensionale Raumes soviel Gleichungen wie es Dimensionen gibt, d.h. für einen Raum mit 100 Dimensionen benötigt man ebenso viele Gleichungen. Doch betrachtet man ein Objekt in diesem Raum, so braucht man zur mathematischen Darstellung nur so viele Gleichungen, wie es der Differenz zwischen der Dimension des Objekts und des Einbettungsraums entspricht. Hat die Einbettung 100 und das Objekt 99 Dimensionen, so braucht man nur 1 Gleichung. Man spricht auch von Codimension. Objekte mit gleicher Codimension haben ähnliche Eigenschaften Ein 1-D-Punkt teilt eine 2-D-Gerade in zwei Stücke, eine 2-D-Ebene teilt einen 3-D-Raum in zwei Hälften und ein Objekt der Codimension 1 teilt einen 33-dimensionalen Raum in zwei Stücke. Die Zweiteilung findet auch statt, wenn man innerhalb einer Dimension diejenige krümmt, die um 1 kleiner ist, wie es in Abb. 18 skizziert ist.

Zum leichteren Verständnis wurde in die gekrümmte Ebene eine dick ausgezogene Hilfslinie eingezeichnet, aus der man erkennt, daß man hier einen ins Unendliche ausgestreckten MÖBIUSring vor sich hat. Die Codimension ist besonders interessant, wenn man nicht so genau weis, wieviel Elemente überhaupt in einer Sache beteiligt sind und die vielleicht sogar wechseln, wobei es dann zu einer unscharfen Menge kommt. Im Allgemeinen bleibt die Eigenschaft der Codimension erhalten, selbst wenn man die 'überflüssigen' Dimensionen wegstreicht. Dies gibt uns die Berechtigung, bei Betrachtung eines höherdimensionalen Objekts, z.B. eines 4-D-Torus im Schnitt mit dem 3-D die topologischen Eigenschaften eines 3-D-Torus zugrunde zu legen. Ein Beispiel in einsehbare Dimensionen ist der Schnitt eines 3-D-Kugel mit einer 2-D-Fläche. Die Codimension ist 3-2=1, d.h. der Schnitt läßt sich durch 1 Gleichung darstellen, obwohl es ein zweidimensionales Objekt ist, nämlich ein Kreis mit der Gleichung U=2r(pi).
9. NICHT-EUKLIDISCHE RÄUME
Als Konsequenz der allgemeinen Relativitätstheorie gibt es keinen starren Körper innerhalb Gravitationsfelder. Während ihrer Bewegung werden die Körper beliebigen Gestaltsänderungen unterzogen, wenn sie sich an anderen Massen vorbeibewegen. Zur Bestimmung der Veränderungen benutzt man das Modell eines nichtstarren Bezugskörpers, " den man nicht mit Unrecht als "Bezugsmolluske" bezeichnen könnte" .
HANS REICHENBACH zeigt in seinem Buch 'Philosophie der Raum-Zeit-Lehre' mit einer Zeichnung, wie, von einem höheren Einbettungsraum aus gesehen, ein Beobachter in einem gekrümmten Raum den Horizont sieht (Abb. 19).

REICHENBACH unterstellt eine sphärische Kugel, obwohl ein gekrümmter Raum torusartig ist. Aber da die Projektion eines Torus auf eine Ebene der einer Kugel gleicht, kann man die Überlegung prinzipiell beibehalten. Um die Konsequenzen zu verallgemeinern, muß man sie allerdings für alle drei Richtungen im 3-D anwenden. In Abb. 19 schaut ein Beobachter von A aus zum Horizont. Die 'Gerade', die ein Lichtstrahl dabei entlangläuft, entspricht der gepunkteten Linie. Wichtig ist der Umstand, daß es auf der anderen Seite des gekrümmten Raumes einen 'Schattenraum' gibt, der für den Beobachter von A aus prinzipiell uneinsehbar ist, ein Umstand, der bisher von den Astronomen in ihren Überlegungen des gekrümmten Universums kaum beachtet wurde!
10. SPIEGELKUGEL-MODELL
Am einfachsten wäre die übliche Reduzierung einer Dimension des 3-D auf eine Ebene, die im Folgenden mit 2-D abkürzen wird, unabhängig davon ob sie plan oder gekrümmt ist.
Aber hier interessiert, was simultan außerhalb und innerhalb eines 3-D geschehen kann, und wie sich 4-D-Ereignisse im 3-D manifestieren können. Dazu benötigt man aber eine räumliche Darstellung des 3-D-Raums innerhalb eines 4-D-Raums. Mit gewissen Einschränkungen sind dazu folgende Modelle brauchbar. Stellt man sich eine verchromte Stahlkugel vor (Abb. 20.), so spiegelt sich auf ihr der gesamte sphärische Raum. Die Abbildung ist zwar verzerrt, aber wenn man auf ihr sehr kleine Flächenstücke herausgreift, kann man die Abweichungen vernachlässigen.

Nun belassen wir die Projektionspunkte auf der Kugel und biegen die Halbschalen nach außen, bis sie zur vorigen Richtung der z-Achse parallel sind. Eine Linie die vorher eine Gerade (G) war, wird dann zur Kurve H in Abb. 20b. Der positive und negative Ast der z-Achse spaltet sich in eine z- und z'-Achse auf . Der Vorteil dieser Version ist, daß man den 3-D mit einer gewissen 'Dicke' darstellen kann und innerhalb der 3-D-Darstellung auch noch die vierte Platz hat.

Die vierte Dimension muß definitionsgemäß auf allen anderen senkrecht stehen, was mit Ausnahme des Trichters überall gegeben ist. In Abb. 21a ist ein Stück dieses Raummodells wiedergegeben. Die z-Achse bildet nun die Deck-'Fläche' des Raumstücks.

Eine Variation des Modells von a ist in b gegeben. Hier wurde die z-Dimension gewissermaßen von Unendlich auf den Wert 1 zusammengequetscht . Der Zahl '+1' entspricht dabei plus Unendlich und '-1' steht für minus Unendlich von z. Der positive Wert der Z-Achse zeigt dabei immer noch nach oben und ist damit parallel zur Darstellung der vierten Dimension v. In dieser Version sind bei Untersuchungen der vierten Dimension nur Eigenschaften der x-y-Ebene in Bezug auf v gültig, ansonsten kann die z-Achse hinzugezogen werden.
Gesetzt der Fall, es gäbe zweidimensionale Wesen, könnten sie auf direktem Wege eine transversale Schwingung einer Ebene nicht wahrnehmen, da die Schwingungsrichtung nicht innerer Teil ihres Systems ist. Für sie sind nur Longitudinalschwingungen direkt erfahrbar. Allerdings gibt es im Falle einer permanenten Transversalschwingung eine besondere Erscheinung in der 2-D-Welt. Die 2-D-Wesen werden entdecken, daß es für sie eine Grenzgeschwindigkeit gibt, die von der Länge des Objektes abhängt. Wenn die Wellenlänge im Vergleich zum Objekt sehr groß ist, werden sie eine Grenzgeschwindigkeit postulieren, die nicht überschreitbar ist. Es ist die Fortpflanzungsgeschwindigkeit der Transversalwelle der Ebene. Im 3-D entspricht dies dem Rumpfwiderstand von Segelbooten im Wasser.
Geht man vom 2-D zum 3-D so gibt es bei einer Einbettung in den 4-D noch eine dritte Schwingungsart. Hier erfolgt die Auslenkung der gesamten 3-D-Raummatrix in Richtung des 4-D, im folgenden 'Matrix-Schwingung genannt (Abb. 23).

Wie schon im Beispiel des 2-D ist auch hier vom 3-D aus auf direkte Weise dieser Schwingungszustand nicht erkennbar; allerdings indirekt, wie schon im vorigen Beispiel. Der Energietransport auf der Basis der Matrixschwingung erfolgt zwar innerhalb des 3-D, aber die Auslenkung nimmt einen Verlauf, der zu allen drei Dimension senkrecht steht. Dabei können im 3-D getrennte Orte verbunden werden, welche im 4-D einen einzigen Energieträger darstellen, beispielsweise in Torusform. Die Matrixschwingung wirkt auch innerhalb der 3-D-Objekte, da das 'Innere' eines Gegenstandes vom 4-D aus offen daliegt, so wie man vom 3-D aus das 'Innere' eines Kreises sehen kann und vom 2-D aus das 'Innere' einer Strecke.
11. DIE FRAKTALE DIMENSION 1.37
Ein interessantes Ergebnis ergaben 1986 Versuche von K. R. SREENIVASAN und C. MENEVAU über die fraktale Dimension von turbulenten Jetströmungen, die von ruhiger Flüssigkeit umgeben sind. Sie kamen auf einen Wert von 1.37 für Turbulenzen auf Ebenen. Diese Ziffernfolge ist Physikern bekannt. "Es war Richard Feynman, in der Tat, der anregte, daß alle Physiker in ihrem Office oder Heim ein Schild aufstellen, um sie daran zu erinnern, wie wenig sie wissen. Auf diesem Schild wäre nur dieses: 137". Diese Ziffernfolge bezieht sich auf die sogenannte ‘Feinstrukturkonstante Alpha’ (*). "Diese Konstante wurde ursprünglich von dem deutschen Physiker Arnold Sommerfeld zu Beginn eingeführt; sie ist eine reine Zahl und muß im Experiment gemessen werden" . Bei Nuklearteilchen ist nicht die gesamte Energie zu Masse verdichtet, 1/137 davon bleibt frei. Es ist die Stärke der elektromagnetischen Wechselwirkung. "Sie ist der Quotient aus dem Quadrat der elektrischen Ladung eines Elektrons und dem Produkt aus Lichtgeschwindigkeit und der Planckschen Konstanten der Quantentheorie ... Wir wissen nicht, warum diese beiden Zahlen genau diese Werte haben. Wären sie anders, wäre auch unser gesamtes Universum anders, vielleicht sogar unvorstellbar anders."
Nun kann es natürlich Zufall sein, daß sich die beiden Werte gleichen. Doch wie ich weiter unten noch zeigen werde, gibt es handfeste Hinweise, daß die Feinstrukturkonstante * mit hoher Wahrscheinlichkeit einen torusförmigen Aufbau der Atome aus Quarks beschreibt. Mit den von K. R. SREENIVASAN und C. MENEVAU durchgeführten Experimenten über turbulente Strahlen beschäftigten sich nämlich schon J. J. THOMSON und H. F. NEWALL. Im Jahr 1885 veröffentlichten sie einen Bericht mit dem Titel "On the Formation of Vortex-Rings by Drops" und 1918 beschrieb EMIL HATSCHEK seine Experimente mit Gelatine, wo er den Nachweise der großen Empfindlichkeit der Formenbildung führte, die von der Dichte der Flüssigkeit bis zur dritten Stelle nach dem Komma abhing . 1877 veröffentlichte A.OVERBECK in "Wiedemanns Analen II" seine Untersuchungsergebnisse von Wirbelbildung in Flüssigkeiten. Allen diesen Forschungen ist ein Ergebnis gemeinsam: Die Wirbelbildung der Strömungen in ruhiger Umgebung erfolgt in Torusform! Daß * die Ziffernfolge 137 hat und nicht 237, wie es für eine dreidimensionale Strömung nötig wäre, könnte ein Hinweis darauf sein, daß diese Dynamik eine geschlossene Kurve auf der Torusform beschreibt, worauf auch der glatte Wert des Spin 1/2 hinweist.
Es gibt noch eine Verbindung zwischen dem Spin 1/2 und der Torusform, die von WHEELER gezeigt wurde. Er erklärt den Zusammenhang anhand eines Würfels, dessen Ecken mittels elastischer Schnüre an Raumecken befestigt sind. Als Modell dafür dient die Projektion eines 4-D-Würfels. Hier kann man einen Würfel als Zimmer ansehen und den anderen Würfel als den zu drehenden. Verbindungsschnüre seien als dünne Linien gegeben.
Dreht man nun den Würfel um eine der drei Mittelachsen um 360°, dann nimmt er zwar wieder die ursprünglliche Lage an, aber die Schnüre sind verdrillt. Erst eine weitere Drehung um nochmals 360°, insgesamt sind es nun 720°, entwirrt die Schnüre wieder. Damit das nicht allzu theoretisch wird, fordert WHEELER uns zu einem 'handgreiflichen' Experiment mit einem Gürtel auf: "Man nehme einen Gürtel und lege ihn flach ausgestreckt auf einen Tisch. Das eine Ende fixiere man, während man das andere Ende um 720° dreht. Nun schiebt man das verdrehte Ende unter Beibehaltung der Orientierung um das andere Ende herum und - der Gürtel ist wieder ausgedreht. Bei einer 360°-Verdrehung ist das nicht so. Der Gürtel steht mit dem Würfel, dem Zimmer und den acht elastischen Schnüren in Beziehung. Bevor man den Würfel überhaupt dreht, kann man ihn aus einem Fenster ziehen. In einiger Entfernung nehmen dann die acht elastischen Schnüre die Form eines Gürtels an."
12. BEISPIEL FÜR FRAKTALE: ELEKTRONENHÜLLE
In den folgenden Kapiteln werde ich noch zeigen, daß es Sinn macht, bei Elektronen die topologische Form eines rotierenden vierdimensionalen Torus anzunehmen, weil damit viele Eigenschaften erklärt werden können, die sonst unbeantwortet bleiben. In der hier vorgeschlagenen Dynamik entsteht eine Asymmetrie in der Kopplung zweier Elektronen. Ein Elektron als dynamischer Torus (Abb. 24) mit Spin 'up' (*) kann wegen der Richtung des Energieflusses ein anderes Elektron auf der ‘Unterseite’ nur innen bei der Zentralachse, auf der ‘Oberseite’ nur außen am Torusumfang ankoppeln, d.h. das andere muß Spin 'down' (*) haben. Dann bilden beide Elektronen zusammen einen geschlossenen Torusring der sich nach innen dreht. Die Kombinationen ** oder ** sind dynamisch nicht möglich.
Ein 4-D-Torus erscheint im Schnitt mit dem 3-D-Raum als Sphäre. Im rechten Teil der Abb. 24 soll somit ein 4-D-Elektronentorus durch eine 3-D-Sphäre symbolisiert werden. In einem Atom ist die erste Elektronenschale (K) mit einem 'up'- und einem 'down'-Elektron abgesättigt. Man findet hier also 2 Elektronen. Das nächste stabile Muster ist durch eine Tetraederform gegeben. Hier sind 4 Sphären zu einer kompakten Figur zusammengefügt. In die Lücken der Vierergruppe passen nochmals vier Sphären in der Orientierung eines umgedrehten Tetraeders und wir sind bei 8 Elektronen angelangt, welche die zweite (L-) Schale abschließen.

Die weiteren Anordnungen sind in Abb. 24 zu skizzieren, es erleichtert aber erheblich das Verständnis, wenn man die Modelle mit richtigen Kugeln konstruiert. Verschiedenfarbige billige Plastikkugeln, die es in jedem Spielzeugladen gibt, reichen dazu völlig aus. Zum Zusammenkleben eignet sich eine Heißklebepistole.
Ist beispielsweise die L-Schale mit 4 weißen und 4 gelben Kugeln zusammengeklebt, so nimmt man für die 18 Elektronen der M-Schale 6 rote und 12 blaue Kugeln. Nun passen zwischen die gelben Kugeln genau 6 rote und anschließend zwischen die roten 12 blaue Kugeln (Abb. 24, 3. Schale). Die blauen Kugeln bilden nun mit jeweils 4 Dreiergruppen die erste fraktale Untergliederung über dem Tetraeder aus den primären weißen Kugeln, bzw. Elektronen.
Mit der N-Schale, die 32 Elektronen hat, geht es ähnlich. 24 grüne Kugeln passen so in die Lücken des Vorläufers, dass am Ende 4 gelbe und 4 weisse Kugeln genau über den Positionen im Kern der 8er-L-Schale zu liegen kommen.
Man sieht hier, dass sich im räumlich-sphärischen 3-D Aufbau der Elektronenhülle, mit den Vorgaben der Quantisierung und dem Aufsuchen des minimalen Energielevels, eine fraktale Entwicklung entfaltet, die aus ineinandergeschachtelten Tetraedern zusammengesetzt ist.
Nun soll das Beispiel nicht dazu verleiten, sich die Elektronen als feste Teilchen vorzustellen. Aber auch wenn man den Wellencharakter berücksichtigt, ist das obige Beispiel anwendbar. Dann stehen die Kugeln für Resonanzknoten der Wellenmuster in der Topologie der Energieverteilung. Mit diesem Modell der Topologie der Elektronenhülle läßt sich auch erklären, warum die Edelgase Neon bis Radon keine Verbindungen mit anderen Elementen eingehen. Ein Elektron mit Spin 'up' und eines mit Spin 'down' bilden jeweils ein Paar. Vier solche Paare bilden ein Tetraeder, welches aus vier gleichseitigen Dreiecken besteht. Durch die gleichen Abstände der Ecken kann die Struktur in Resonanzschwingung geraten, welche eventuelle Verbindungen mit anderen Atomen abreißen lässt. Im Heliumatom bilden die 2 Protonen und 2 Neutronen einen Tetraeder.
-
nicole6

- ModeratorIn

- Beiträge: 2333
- Registriert: 11.09.2009, 13:01
- Wohnort: München
- Ich bin: ehemalige SexarbeiterIn
RE: Diskussionspapier: Modell für Zeit und Raum
13. PHOTONEN.
Es besteht eine große Verwirrung in der synonymen Verwendung der Begriffe 'Licht' und 'Photonen'. Ein Photon ist ein einzelnes und quantisiertes Energiepartikel. Seine Energie ist durch einen einzigen Parameter gegeben: die Frequenz. Es ist elektrisch neutral, ohne Masse und hat den Spin 1, d.h. im hier vorgestellten Modell des Torus ist das Verhältnis der Drehungen um beide Torusachsen L und R 1:1.
Von der Regel, daß jedes Teilchen sein separates Antiteilchen hat, macht das Photon eine Ausnahme, denn es ist sein eigenes Antiteilchen. Die daraus folgenden Konsequenzen wurden bisher von wenigen Forschern beachtet. Teilchen und Antiteilchen unterscheiden sich durch die Zeitrichtung. Ein Teilchen wie das Photon, das beide Zeitrichtungen umfaßt, hat logischerweise im 3-D keine Geschwindigkeit: " Zum Beispiel, wir hören manchmal die Aussage, daß ein Lichtsignal von einem Teil der Raumzeit zu einem anderen abgesendet wurde. Die korrekte Ausdrucksweise für diesen Sachverhalt ist zu sagen, daß das Lichtsignal (spannungslos) entlang einer Linie zwischen diesen beiden Teilen der Raumzeit liegt." MICHAEL SHALLIS formuliert es so: “Wenn sich die Zeit in Annäherung an die Lichtgeschwindigkeit verlangsamt, kann man davon ableiten, daß für ein Photon, ein Lichtpartikel, Zeit nicht existiert. Zu diesem Ausmaß kann ein Photon rund um das Universum in Null-Zeit reisen, weil es in seinen Referenzrahmen keine Zeit gibt.”
Photonen sind quantisiert. Der Übertragungsmechanismus dieser Quanten ist aber noch sehr unklar. "Wenn Begriffe nicht anschaulich sind, sind sie noch nicht geklärt. In der Quantenoptik sind sie nicht anschaulich, also sind sie noch nicht geklärt" .
Photonen interagieren nicht miteinander! Ansonsten könnten wir nichts sehen, da sich die Photonen gegenseitig vernichten würden. In einem Raum können sie ungestört jeden Punkt des Raumes mit jedem anderen verbinden. Interaktion, d.h. Interferenz geschieht nicht mit anderen Photonen, sondern mit Masse-besetzten Objekten. Wenn die Zahl der einzelnen Photonen auf einer Brom-Silberschicht energetisch ausreicht das Brom vom Silber zu trennen, wird das Silber frei und wenn man das Brom abwäscht, wird ein schwarzer Silberpunkt sichtbar. Wenn nicht, bleibt die Stelle weiß. Aber untereinander gibt es keine Interferenz.
Der Begriff 'Licht' wird allgemein im Sinn verwendet, daß eine große Zahl von Photonen am Prozeß beteiligt sind, von denen jedes einzelne keine Geschwindigkeit hat und keines mit irgend einem anderen interagiert. "Eine gewöhnliche Glühbirne emittiert in einer milliardstel Sekunde mehr als 100 Milliarden von ihnen." Wenn aber die Geschwindigkeit eines Photons Null ist, dann ist die von einer Billion Photonen ebenfalls Null, denn eine Billion mal Null ist und bleibt Null.
14. 'LICHTGESCHWINDIGKEIT'.
Wie konnte es aber zum Begriff 'Lichtgeschwindigkeit' kommen? Ein Grund ist sicher der, daß die Forscher durch jahrhundertelange Rezeption griechischer Philosophen so hypnotisiert waren, daß sie zwangsläufig ‘Zeit’ und ‘Werden’ mit 'Geschwindigkeit' verbanden. Das krampfhafte Festhalten an der Vorstellung des dreidimensionalen Raumes als Existenzgrundlage tat das übrige dazu. So sahen sie Geschwindigkeiten, wo nur Veränderungen waren und ignorierten geflissentlich Beweise, die auf höherdimensionale Räume hinwiesen. Probleme gab es schon früh, als 1887 ALBERT MICHELSON und EDWARD MORLEY versuchten die 'Lichtgeschwindigkeit' zu messen. Zu ihrer Überraschung waren die 'Geschwindigkeiten' immer gleich, egal in welchem relativen Bewegungszustand man sich zur Lichtquelle befand.
Um das Problem einsichtig zu machen, reduziert man die Dimensionen um eine und betrachtet ein zweidimensionales Geschehen im 2-D. Die Ereignisse im 2-D-Land seien auf einem Film festgehalten, welche einsichtige Wesen im 3-D im Kino anschauen. Der Film im Projektor soll beispielsweise 30 Bilder pro Sekunde vorrücken und die Projektion auf der Leinwand habe 10 Meter Durchmesser. Offensichtlich verändern sich die Dinge im 2-D-Universum und die Wissenschaftler auf der Leinwand bemühen sich nun, die Geschwindigkeit von Lichtstrahlen zwischen zwei Punkten zu messen. Aber egal wie sie messen, die 'Geschwindigkeit' ist immer die Gleiche, sie ist 300 Meter pro Sekunde, egal in welche Richtung sie sich in ihrem 2-D bewegen. Und was sie noch feststellen, diese 300 m/sec sind eine Art 'Grenzgeschwindigkeit', die nicht zu übertreten ist. In ihrem 2-D kann kein Signal von einem Punkt der Leinwand früher zu einem anderen Punkt kommen als nach 1/30 Sekunde (Abbildung 25).
Vom 3-D aus wird der Sachverhalt jedoch klar und ist nicht mehr mysteriös. Wenn eine Person beispielsweise einen Stern erblickt, dann verbindet ein Photon den Stern und das Auge für diesen Augen-Blick. Es gibt keine wirkliche Bewegung der Zeit, in der sich eine Bahn von dem Stern bis zu meinem Auge entwickelt; das ist nur meine Wahrnehmung von meinem Standpunkt aus. Von einem anderen, ebenso gültigen Standpunkt aus ist die Bahn eine ewige Erscheinung, um die herum das Universum sich verändert, und im Laufe dieser Veränderungen im Universum kommt es unter anderem dazu, daß sich mein Auge und der Polarstern zufällig an den entgegengesetzten Enden der Bahn befinden."
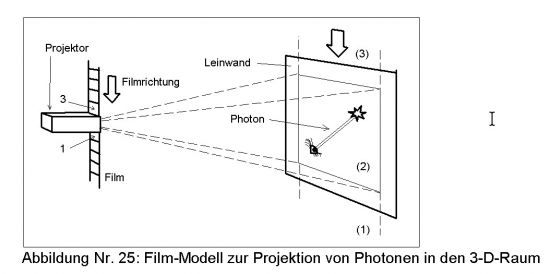
Wenn Forscher Ortsveränderungen im Lichtbereich messen, ermitteln sie demnach nicht die 'Lichtgeschwindigkeit' im 3-D, sondern die Geschwindigkeit der Raum-Matrixwellen im 4-D-Raum. Jedes einzelne Photon stellt dabei eine ruhende Verbindungsstrecke im 3-D dar. In diesem Modell besteht somit kein Widerspruch zwischen der Existenz der Photonen außerhalb der Zeit und auf der anderen Seite sichtbaren Veränderungen im 3-D.
Wenn Forscher Ortsveränderungen im Lichtbereich messen, ermitteln sie demnach nicht die 'Lichtgeschwindigkeit' im 3-D, sondern die Geschwindigkeit der Raum-Matrixwellen im 4-D-Raum. Jedes einzelne Photon stellt dabei eine ruhende Verbindungsstrecke im 3-D dar. In diesem Modell besteht somit kein Widerspruch zwischen der Existenz der Photonen außerhalb der Zeit und auf der anderen Seite sichtbaren Veränderungen im 3-D.
Auch für die Komplementäreigenschaften Licht/Welle des Photons ist das 4-D-Modell verwendbar und die Erscheinung eines Photons als Welle oder ein anderes Mal als Teilchen wird unmittelbar einleuchtend.
Die horizontale Ebene in Abb. 26 stellt den um eine Dimension reduzierten 3-D dar. Eine Lichtwelle welche im 4-D die 4-D-Punkte C und D verbindet, schneidet den 3-D in Z und erscheint dann dort als Teilchen. Die gleiche Welle kann aber auch die 4-D-Punkte A und B verbinden, die zudem im Schnitt mit dem 3-D liegen. In diesem Fall wird der Wellencharakter erkennbar. Welcher von den beiden Zuständen sich manifestiert, entscheidet die Vorrichtung. Jedes Photon wird bei der Messung vernichtet. Man kann es also nur einmal messen, entweder als 'Teilchen' oder als 'Welle'.
15. ROTVERSCHIEBUNG.
VESTO M. SLIPHER präsentierte 1914 der Tagung der Astronomischen Gesellschaft die ersten genauen Spektralanalysen von Sternen, wobei sich herausstellte, daß die Linien gegenüber denen im Labor hergestellten, stark verschoben waren. Dies wurde als 'DOPPLEReffekt' interpretiert und EDWIN HUBBLE veröffentlichte zwischen 1925 und 1929 die ersten Arbeiten darüber, wobei als Grundlage die Idee war, dass diese Verschiebung der Spektrallinien zum roten Bereich hin für ein expandierendes Universum sprach. "aber er akzeptierte nie völlig, daß die Rotverschiebung nur von der Radialgeschwindigkeit der Galaxien herrühren sollte."
Wenn man die Konsequenzen der Quantenphysik akzeptiert, stimmt das auch. Das Problem, welches das Wesen der Quantensprünge illustriert, ist der Übergang eines Elektrons von einer Schale der Atomhülle auf eine andere Schale. In Abb. 27a ist ein Übergang eines Elektrons von der K-Schale zur L-Schale skizziert. Dabei gibt es die überflüssige Energie in Form eines Photons ab.
Würden die klassischen Gesetze gelten, dann müßte zwischen dem Aufenthalt in L und der Ankunft in K eine Zeitunterschied zwischen den Zeitpunkten 1 und 2 nachweisbar sein, wie es die untere Kurve in Abb. 67b zeigt. Auf der unteren Achse ist der Abstand zwischen den Elektronenschalen K und L aufgetragen, nach oben die Zeit. Durch die Bewegung würde sich der Energiezustand ändern, der sich durch eine Verbreiterung der Spektrallinie der abgesendeten Photonen zeigen müßte. Dies ist aber nicht der Fall! Also muß der Wechsel der Bahnen in 'Nullzeit' stattfinden, was die obere Linie von Abb. 67b zeigt. "Diese scheinbar einfache Vorstellung bedeutete in Wirklichkeit einen tiefen Bruch mit den klassischen Vorstellungen. Es ist, als würde der Mars aus seiner Bahn verschwinden, unverzüglich in der Bahn der Erde wieder auftauchen und dabei einen Energiestrom ... in den Raum strahlen." Die abgestrahlte Energie ist dabei in feste Größen gepackt und wird sofort, ohne Zeitdifferenz abgegeben! "Man hätte solche Vorstellungen wohl nie ernst genommen, wenn man nicht damit eine ganze Reihe von Experimenten hätte sehr gut und genau erklären können."
Der DOPPLEReffekt
In Abb. 28 ist ein Objekt gegeben, welches sich in einem Medium z.B. Luft bewegt und dabei Schallwellen erzeugt. Wenn das Objekt ruht, breiten sich die Wellen konzentrisch in sphärischer Form aus. Wenn sich das Objekt dabei bewegt, entsteht zwischen der Eigenschwindigkeit des Objektes und der Geschwindigkeit der Schallwellen eine Differenz. Da Schallwellen aber Longitudinalwellen sind, addieren, bzw. subtrahieren sich die Geschwindigkeiten und ein Beobachter von vorne (3) nimmt eine höhere Frequenz war, als sie vom Objekt erzeugt wird. Dahinter (2) erscheint sie tiefer und nur ein seitlicher Beobachter (1) hört die ursprüngliche Frequenz. Ohne das Medium Luft verschwindet der DOPPLEReffekt sofort, da es dann auch keinen Schall mehr gibt. Wichtig ist auch die Schallaussendung in der Zeit und addier- bzw. subtrahierbare Geschwindigkeiten von Objekt und Wellenausbreitung. Beobachter 1 befindet sich rechtwinklig zum Geschehen, weshalb in diesem Zeitpunkt der Dopplereffekt für ihn nicht erfahrbar ist.
Nun wendet man das Ganze auf Licht an. Ende des 19. Jahrhunderts wurde noch über ein Trägermedium für Licht diskutiert, der sogenannte 'Äther', der heute für die Physiker das ist, was der Teufel für den Pfarrer darstellt (wer vom 'Äther' spricht, muß verrückt sein, und diese Besessenheit muß man der Person am besten austreiben). Da es aber nun kein Trägermedium für Licht geben darf, fällt der erste Punkt zur Erzeugung des Dopplereffekts weg.
Wenden wir uns dem nächsten Punkt zu, der Addition und Subtraktion von Geschwindigkeiten. Die Versuche von MICHELSON und MORLEY 1887 zeigten, daß bei einer angenommenen Geschwindigkeit von Licht diese immer gleich ist, egal in welcher relativen Geschwindigkeit man sich dazu bewegt! Anders ausgedrückt, sie ist unabhängig von irgend einem Bewegungszustand im 3-D. Damit ist es aber auch nicht erlaubt, die Geschwindigkeit des lichtaussendenden Objekts von der angeblichen Lichtgeschwindigkeit abzuziehen oder dazuzuzählen. Dies verletzt im Kern die Relativitätstheorie von EINSTEIN. Und wem das noch nicht reicht, der kann noch die Quantenphysik hinzuziehen.
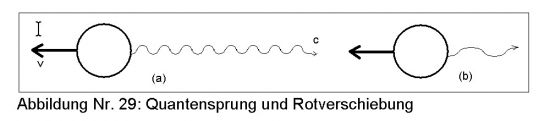
Die Aussendung eines Gammaquants (Photons) erfolgt durch einen Quantensprung eines Elektrons der Atomhülle, in dem das gesamte Photon auf einmal abgeschickt wird (Abb. 29a). Dabei ist aber keine Frequenzänderung möglich, da diese eine Zeitdifferenz erfordert. Geht man aber von einer Verlängerung der Frequenz des Photons aufgrund der Eigengeschwindigkeit v des Objektes aus, so muß die Aussendung des Photons in einer endlichen Zeitdifferenz erfolgen, d.h. die Photonenwelle muß in der Zeit Schwingung für Schwingung das Objekt verlassen (Abb. 29b). Dies verletzt aber die Quantenbedingungen und im Experiment müßte man breite Spektrallinien sehen, was nicht der Fall ist.
Als viertes betrachten wir die Sache auf der mathematisch-physikalischen Ebene. Als Welle ist jedes einzelne Photon unendlich lang ausgedehnt, aber die Geschwindigkeit mit dem Wert 'Unendlich pro Sekunde' gibt es nicht. Das Photon verbindet in Wellenform einfach zwei Punkte im Raum miteinander. Photonen interagieren im freien Raum nie miteinander, sondern nur innerhalb eines Masseobjektes. Als Partikel hat das Photon die Energie im Drehimpuls gespeichert, wobei dieser Impuls genau der Frequenz des Photons proportional ist. Drehimpulse sind aber unabhängig von linearer Geschwindigkeit. Nimmt man in einem Auto einen schwarzen Kreisel mit und markiert den Rand mit einem weißen Strich, so können sowohl die Passagiere wie auch Passanten auf der Straße genau die Anzahl der Drehungen zählen. Die linearen Bewegungen ändern nichts am Drehimpuls des Kreisels.
Fazit: Die 'Theorie' über die Rotverschiebung auf Grund einer angeblichen 'Fluchtgeschwindigkeit' der Sterne ist in allen Aspekten falsch!
Der Astrophysiker JAMES TREFIL schreibt dazu: "Ich erinnerte mich an einen Imbiß in einem angesehenen physikalischen Institut, bei dem ein sehr prominentes Mitglied dieser Fakultät (ich würde es nicht wagen, ihn durch die Erwähnung seines Namens in Verlegenheit zu bringen) sagte, er spiele oft mit dem Gedanken, einen versiegelten Umschlag zu hinterlassen, der fünfzig Jahre nach seinem Tod geöffnet werden solle. Er enthielte seine Vorhersagen über die Ergebnisse bestimmter wissenschaftlicher Kontroversen. An erster Stelle der Liste, fuhr er fort, stünde die Vorhersage, die Interpretation der Rotverschiebung als Beweis für die Ausdehnung des Universums würde sich als falsch erweisen."
Kritik an der Rotverschiebung äußerte 1952 MAX BORN in einem Brief an ALBERT EINSTEIN , als er schrieb: "Es sieht wirklich so aus, als ob Deine Formel nicht ganz stimmt. Bei der Rotverschiebung sieht es noch schlimmer aus; im Inneren der Sonnenscheibe ist sie viel kleiner, am Rand größer als der theoretische Wert" .
Spektralverschiebung als Raumkrümmungseffekt
ERNST MACH erwähnt in einer Bemerkung, daß er bei der Überlegung für eine Erklärung der Linienspektren die Idee hatte, daß nichtsinnliche Dinge nicht notwendigerweise im sinnlich wahrnehmbaren dreidimensionalen Raum vorgestellt werden müssen: "So kam ich auf Analoga des Raumes von verschiedener Dimensionszahl" . Akzeptiert man höherdimensionale Räume als existent, so gibt es eine einfache Erklärung für vorhandene Rotverschiebung von Lichtspektren, die sogar unterschiedliche Verschiebungen bei Doppelsternen mit einschließt. Als Raummodell nehme ich die Konstruktion von Abb. 30 als Basis.
Da vierdimensionale Raumkonstruktionen nicht gerade üblich sind, werde ich zur Eingewöhnung ein Beispiel vorschalten, welches sich im einsehbaren 2-D abspielt.

Der gekrümmt 2-D hat, wie ich schon oben zeigte, die Form eines Torus im 3-D-Einbettungsraum. Projiziert man die Torusoberfläche auf den 2-D wie in Abb. 30a , so erhält man einen Kreis mit Mittelpunkt, wenn man einen Torus mit Lochdurchmesser Null gewählt hat, ansonsten ist es ein Kreisring. Im Querschnitt erzeugte der Torus im 2-D zwei getrennte Kreise. Die Projektion auf die Ebene ist aber doppelt, da die Ebene den Torus in zwei Hälften schneidet (siehe auch Abschnitt über Kodimension). Legt man auf dem Torus in gleichen Abständen Umfänge an, so erscheinen diese an den Rändern und zur Mitte der Kreisprojektion verdichtet (Abb. 30b). Würde man Volumenelemente des Torus auf den Kreis projizieren, hätten diese die umgekehrte Charakteristik, sie wären zur Mitte hin dichter als nach außen.
Bei der Projektion des 4-D-Hypertorus in dem dreidimensionalen Raum geschieht etwas ähnliches. Der Hypertorus erscheint im 3-D als Kugel mit Mittelpunkt wie in Abb. 30a. Eine einzige Ebene der Hypertorus, wie in Abb. 30b, entspricht in der 3-D-Projektion schon einer ganzen Kugel! Eine analoge Erscheinung hätte man im 2-D. Zweidimensionale Wesen würden ein Kugel als 'Hyperkreis' bezeichnen, wobei ein einziger Kugelschnitt schon einen kompletten Kreis ausfüllt, aber damit hätte man die Kugel genausowenig umfassend beschrieben, wie im vierdimensionalen Fall mit der Kugel den Hypertorus. Der senkrechte Schnitt in Abb. 31a ist ebenfalls ein gültiger Teil des Hypertorus. Die Durchdringung mit der horizontalen Projektion ist nur scheinbar, denn in der 4-D-Wirklichkeit sind sie getrennt.
Wenn nun Licht, wie oben gezeigt wurde, eine Erscheinung des 4-D ist, dann ist die Ausbreitung der Photonen nicht an den 3-D gebunden und sie können auch von außen in den von uns sichtbaren Raum eindringen. Dabei müssen sie sich der Raummatrix anpassen und erfahren eine Wellenlängenänderung, die in Abb. 32 skizziert ist.
Auf der linken Seite sollen sich im gekrümmten 3-D an einer weit entfernten Stelle Doppelsterne oder Quasare befinden. Vom lokalen Beobachter aus kann die Entfernung täuschen, da die Lichtquelle im gleichen Raumsektor 'nah' erscheinen mag. Dies kann aber ein Effekt des gekrümmten Raumes sein, so wie in Abb. 31 auf dem Torus weit auseinanderliegende Punkte in der Projektion nahe beieinander zu liegen scheinen. Indem das Licht die 'Abkürzung' durch den 4-D nimmt, hat es einen gewissen Winkel beim Wiedereintritt in den 3-D und muß sich dort der Raumstruktur anpassen. Um sich nicht von der Skizze irreführen zu lassen, muß man sich daran erinnern, daß vom 4-D aus der 3-D komplett offen vor einem liegt. Man kann dann auch z.B. von innen in Objekte einsehen.
In Abb. 32b sieht man, daß die Wellenlänge des Lichts beim durchkreuzen des 3-D eine Verlängerung erfährt, da die ursprüngliche Länge einer Kathede und der Abstand im 3-D der Hypothenuse eines rechtwinkligen Dreiecks entspricht. Bei gleicher Kathede verlängert sich die Hypothenuse mit zunehmendem Einfallswinkel vom 4-D. Je paralleler der Winkel, um so weniger geht die Wellenlängenverschiebung zum roten Bereich. Bei diesem Modell des Universums ist es notwendig, daß Doppelsterne, die im Bezug zu einem bestimmten Beobachter unterschiedliche Winkel aufweisen, unterschiedliche Rotverschiebung haben. Damit könnte man die Daten von verschiedenen Quasaren erklären.
Aber dieser Effekt könnte auch innerhalb des 3-D-Raumes auftreten, wenn nämlich durch große Masseanhäufungen der Raum in sich gekrümmt ist. Zwar ist innerhalb des 3-D diese Krümmung nicht direkt erfahrbar, aber von einem Beobachter außerhalb des 3-D würde dies durch eine Verdichtung der Raummatrix erkennbar sein. Da Photonen aber 4-D-Erscheinungen sind, treffen sie dann vom 4-D aus in einem Winkel zur 3-D-Raummatrix am Beobachtungsort ein und erfahren dort in gleicher Weise wie in Abb. 32 eine Verlängerung der Wellenlänge.
Mit diesem Modell könnte man die Eigenschaften des Quasars 3 C 279 als Zweikomponentensystem erklären, über die P.STUBBS berichtete , dessen beiden Komponenten sich angeblich ‘auseinanderbewegen’. Wenn man die Rotverschiebung als Fluchtgeschwindigkeit interpretiert, kommt man auf das zehnfache der 'Lichtgeschwindigkeit'. Ebenfalls hätte man Erklärungen für die von HALTON ARP gefundenen Galaxienpaare, deren Teile aufgrund der bisher geltenden Theorien unterschiedliche Geschwindigkeiten haben müßten, die sich um das zehnfache unterscheiden. Das ist, als würde man behaupten, bei einem Fahrrad würde das Vorderrad sich mit 10 km/h und das Hinterrad mit 100 km/h bewegen. In 16 Fällen fand ARP bei jüngeren Tochtergalaxien eine höhere Rotverschiebung als bei den älteren Muttergaklaxien. Die erste Reaktion der Astronomen war, daß sie diese Beobachtung als 'optische Täuschung' bezeichneten. "Der Widerstand der Astronomen, ihre Beobachtungszeit auf die Verfolgung der Gedanken Arps zu verwenden, ist vielleicht analog zu der Abneigung zu sehen, die fast alle Wissenschaftler gegen den ‘siebten Sinn', die außersinnliche Wahrnehmung, hegen."
16. LICHTBRECHUNG IN DURCHSICHTIGEN OBJEKTEN
In den Physikbüchern steht, daß in durchsichtigen Körpern die 'Lichtgeschwindigkeit' c eine Funktion der Frequenz sei. Die daraus folgende Abhängigkeit der Brechzahl n eines Körpers von der Frequenz nennt man Dispersion. Die unterschiedlichen 'Geschwindigkeiten' des Lichts im Glas seien angeblich auch für die Brechung (Abb. 33a) verantwortlich. Läßt man einmal den Punkt beiseite, daß die Photonen keine Geschwindigkeit haben, so ergibt sich ein weiterer Widerspruch mit der Erklärung des Verhaltens von Licht an einer planparalleln Platte (Abb. 33b). Hier, so heißt es, werde das Licht nur parallel verschoben, gehe aber ansonsten unverändert durch. Den Widerspruch erkennt man durch zwei aneinandergelegte Prismen (Abb. 33c).
Diese zwei Prismen ergeben eine planparallele Platte, also dürfte sich das Licht nicht aufspalten. Da es aber Prismen sind, müßte die Aufspaltung trotzdem stattfinden. Und, was interessant ist, das Licht müßte am Anfang beim Eintreten schon 'wissen', welchen Winkel die andere Glasseite hat, um sich zu entscheiden ob der Strahl aufgespalten wird oder nicht. Nun könnte man kommen und sagen, die Aufspaltung finde zwar immer statt, aber der Effekt sei so klein, daß man ihn vernachlässigen könne. Das stimmt leider nicht. Bei Flintglas, das einen großen Dispersionsindex hat, müßte man den Effekt bei nur 1 cm dicken Glas schon mit bloßem Auge sehen, denn die Aufspaltung müßte ca 1/10 Millimeter sein (!), etwa in der Größenordnung der Breite eines Millimeterstrichs auf einem Meßband.
Ein weiteres Beispiel dazu: wenn die Aussage über verschiedene Brechungswinkel wegen unterschiedlicher Geschwindigkeiten stimmen würde, dann müßten sich in einem langen Glasfaserkabel bei jeder Reflexion an der Glaswand die roten und violetten Strahlen voneinander entfernen. Aus einem kompakten Strahl am Anfang des Glaskabels müßte dann am Ende ein breites Regenbogenspektrum werden.
Auf gleicher Ebene befindet sich das Problem der partiellen Reflexion an einer Glasoberfläche. Läßt man 100 Photonen auf eine Glasoberfläche los, dann gehen 96 durch und vier kommen zurück. "Und damit fangen unsere Schwierigkeiten bereits an: Wie ist es überhaupt möglich, daß Licht nur teilweise reflektiert wird? Das eine Photon landet in A, das andere in B - wie 'entscheidet' es sich, wohin es will?" RICHARD FEYNMAN schreibt, daß seine Zuhörer auf diese Bemerkung hin lachten. Er meinte, daß es wie ein Witz klingen mag, aber mit Lachen sei es nicht getan. Hier hat man es mit einem Beispiel zu tun, wo eine gleiche Voraussetzung zu unterschiedliche Resultaten führt. Bei einem einzelnen Photon läßt es sich nicht voraussagen, ob es durch das Glas geht, oder ob es reflektiert wird. Und trotzdem sind am Ende bei hundert Photonen 96 durchgelassen worden und 4 kamen zurück. Die Frage ist nun, woher weiß das fünfzigste Photon, ob es das fünfzigste ist oder das erste oder das hundertste, um entweder durchzugehen oder nicht, damit am Ende die Statistik der Forscher stimmt? Da Photonen ihre eigenen Antiteilchen sind, muß man jede Verbindung die sie herstellen, von beiden Seiten betrachten können. Offensichtlich muß die Frage anders gestellt werden.
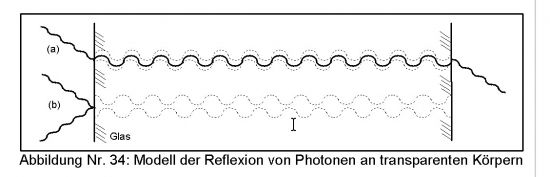
Mit der Annahme eines 4-D-Raumes und der zugehörigen Matrixschwingung des uns zugänglichen 3-D in Richtung 4-D, gibt es einen Weg aus dem Problem. Die weitere Voraussetzung ist ein Quantenverhalten des Systems. Ein Stück Masse, in diesem Fall Glas, ist den permanenten 4-D-Matrix-Schwingungen des Raumes ausgesetzt, wobei sich die Atomstruktur diesen Bewegungen anpassen muß. Aufgrund innerer Masseverhältnisse und Quantenverhalten wird bevorzugt ein Zustand eingenommen, bei dem die Materiewellen an der Oberfläche Knoten haben. Dies entspricht einer schwingenden Gitarresaite (Abb. 34a). Kurzzeitig wird allerdings der Energiebetrag zur Aufrechterhaltung dieser Frequenz über- oder unterschritten, und eine neue Quantenschwingung stellt sich ein, deren Länge aber inkompatibel mit der Distanz der Brechungsflächen ist. Dadurch sind keine Knoten an der Oberfläche, sondern Schwingungsbäuche, welche den Durchgang von Photonen verhindern (Abb. 34b), ähnlich wie ein drehender Ventilator Objekte zurückwirft.
Man könnte den Prozeß auch mit einem Klavier vergleichen. Setzt man als Analogie für die Durchgangsbedingungen die Oktaven einer Frequenz, z.B. das 'c', dann wird die Passage gesperrt, wenn bei einer der Oktaven aus dem 'c' ein 'h' oder 'cis' wird. In dieses Modell paßt auch die Erfahrung aus der Optik, daß dünne aufgedampfte Metallschichten den Durchgang einer bestimmten Frequenz ermöglichen, den von anderen jedoch blockieren. Wenn die Schichtdicke der Wellenlänge entspricht, schwingt der Raum an der Stelle mit Knoten an den Endflächen und ermöglicht den Photonen den Durchgang.
Sind die Endflächen zueinander geneigt, wie beim Prisma, dann sind von jedem Eintrittspunkt des Glases aus, den unterschiedlichen Längen der Wellen entsprechend, quantisierte Strecken zum Austritt möglich, die sich fächerförmig aufspalten (Abb 35). Bei einer planparallelen Platte ist dies nicht möglich, da hier die Raummatrix parallel schwingt.
Das Brechungsgesetz muß dann neuformuliert so heißen: Die Raummatrix in festen (flüssigen, gasförmigen ) Objekten schwingt langsamer als im Vakuum. Liegt innerhalb eines Lichtstrahls ein durchsichtiger Körper, so verkürzt dieser durch die von ihm verursachte Raumkrümmung den Abstand zwischen Lichtquelle und Auftreffpunkt. Die Verbindung des Lichtstrahls von der Quelle zum Objekt erfolgt zu Zeitpunkten, an denen die Raummatrix an der Oberfläche des durchsichtigen Körpers Knoten hat. Ist dort ein Schwingungsbauch, wird das auftreffende Photon reflektiert und folgt der Struktur der äußeren Raummatrix. Die Wellenlänge innerhalb des durchsichtigen Körpers hängt vom Material ab. Der Prozentsatz an reflektierten Photonen hängt vom Prozentsatz der Zeit ab, in welcher der Raum an der Grenzfläche Schwingungsbäuche statt Schwingungsknoten hat.
Es besteht eine große Verwirrung in der synonymen Verwendung der Begriffe 'Licht' und 'Photonen'. Ein Photon ist ein einzelnes und quantisiertes Energiepartikel. Seine Energie ist durch einen einzigen Parameter gegeben: die Frequenz. Es ist elektrisch neutral, ohne Masse und hat den Spin 1, d.h. im hier vorgestellten Modell des Torus ist das Verhältnis der Drehungen um beide Torusachsen L und R 1:1.
Von der Regel, daß jedes Teilchen sein separates Antiteilchen hat, macht das Photon eine Ausnahme, denn es ist sein eigenes Antiteilchen. Die daraus folgenden Konsequenzen wurden bisher von wenigen Forschern beachtet. Teilchen und Antiteilchen unterscheiden sich durch die Zeitrichtung. Ein Teilchen wie das Photon, das beide Zeitrichtungen umfaßt, hat logischerweise im 3-D keine Geschwindigkeit: " Zum Beispiel, wir hören manchmal die Aussage, daß ein Lichtsignal von einem Teil der Raumzeit zu einem anderen abgesendet wurde. Die korrekte Ausdrucksweise für diesen Sachverhalt ist zu sagen, daß das Lichtsignal (spannungslos) entlang einer Linie zwischen diesen beiden Teilen der Raumzeit liegt." MICHAEL SHALLIS formuliert es so: “Wenn sich die Zeit in Annäherung an die Lichtgeschwindigkeit verlangsamt, kann man davon ableiten, daß für ein Photon, ein Lichtpartikel, Zeit nicht existiert. Zu diesem Ausmaß kann ein Photon rund um das Universum in Null-Zeit reisen, weil es in seinen Referenzrahmen keine Zeit gibt.”
Photonen sind quantisiert. Der Übertragungsmechanismus dieser Quanten ist aber noch sehr unklar. "Wenn Begriffe nicht anschaulich sind, sind sie noch nicht geklärt. In der Quantenoptik sind sie nicht anschaulich, also sind sie noch nicht geklärt" .
Photonen interagieren nicht miteinander! Ansonsten könnten wir nichts sehen, da sich die Photonen gegenseitig vernichten würden. In einem Raum können sie ungestört jeden Punkt des Raumes mit jedem anderen verbinden. Interaktion, d.h. Interferenz geschieht nicht mit anderen Photonen, sondern mit Masse-besetzten Objekten. Wenn die Zahl der einzelnen Photonen auf einer Brom-Silberschicht energetisch ausreicht das Brom vom Silber zu trennen, wird das Silber frei und wenn man das Brom abwäscht, wird ein schwarzer Silberpunkt sichtbar. Wenn nicht, bleibt die Stelle weiß. Aber untereinander gibt es keine Interferenz.
Der Begriff 'Licht' wird allgemein im Sinn verwendet, daß eine große Zahl von Photonen am Prozeß beteiligt sind, von denen jedes einzelne keine Geschwindigkeit hat und keines mit irgend einem anderen interagiert. "Eine gewöhnliche Glühbirne emittiert in einer milliardstel Sekunde mehr als 100 Milliarden von ihnen." Wenn aber die Geschwindigkeit eines Photons Null ist, dann ist die von einer Billion Photonen ebenfalls Null, denn eine Billion mal Null ist und bleibt Null.
14. 'LICHTGESCHWINDIGKEIT'.
Wie konnte es aber zum Begriff 'Lichtgeschwindigkeit' kommen? Ein Grund ist sicher der, daß die Forscher durch jahrhundertelange Rezeption griechischer Philosophen so hypnotisiert waren, daß sie zwangsläufig ‘Zeit’ und ‘Werden’ mit 'Geschwindigkeit' verbanden. Das krampfhafte Festhalten an der Vorstellung des dreidimensionalen Raumes als Existenzgrundlage tat das übrige dazu. So sahen sie Geschwindigkeiten, wo nur Veränderungen waren und ignorierten geflissentlich Beweise, die auf höherdimensionale Räume hinwiesen. Probleme gab es schon früh, als 1887 ALBERT MICHELSON und EDWARD MORLEY versuchten die 'Lichtgeschwindigkeit' zu messen. Zu ihrer Überraschung waren die 'Geschwindigkeiten' immer gleich, egal in welchem relativen Bewegungszustand man sich zur Lichtquelle befand.
Um das Problem einsichtig zu machen, reduziert man die Dimensionen um eine und betrachtet ein zweidimensionales Geschehen im 2-D. Die Ereignisse im 2-D-Land seien auf einem Film festgehalten, welche einsichtige Wesen im 3-D im Kino anschauen. Der Film im Projektor soll beispielsweise 30 Bilder pro Sekunde vorrücken und die Projektion auf der Leinwand habe 10 Meter Durchmesser. Offensichtlich verändern sich die Dinge im 2-D-Universum und die Wissenschaftler auf der Leinwand bemühen sich nun, die Geschwindigkeit von Lichtstrahlen zwischen zwei Punkten zu messen. Aber egal wie sie messen, die 'Geschwindigkeit' ist immer die Gleiche, sie ist 300 Meter pro Sekunde, egal in welche Richtung sie sich in ihrem 2-D bewegen. Und was sie noch feststellen, diese 300 m/sec sind eine Art 'Grenzgeschwindigkeit', die nicht zu übertreten ist. In ihrem 2-D kann kein Signal von einem Punkt der Leinwand früher zu einem anderen Punkt kommen als nach 1/30 Sekunde (Abbildung 25).
Vom 3-D aus wird der Sachverhalt jedoch klar und ist nicht mehr mysteriös. Wenn eine Person beispielsweise einen Stern erblickt, dann verbindet ein Photon den Stern und das Auge für diesen Augen-Blick. Es gibt keine wirkliche Bewegung der Zeit, in der sich eine Bahn von dem Stern bis zu meinem Auge entwickelt; das ist nur meine Wahrnehmung von meinem Standpunkt aus. Von einem anderen, ebenso gültigen Standpunkt aus ist die Bahn eine ewige Erscheinung, um die herum das Universum sich verändert, und im Laufe dieser Veränderungen im Universum kommt es unter anderem dazu, daß sich mein Auge und der Polarstern zufällig an den entgegengesetzten Enden der Bahn befinden."

Wenn Forscher Ortsveränderungen im Lichtbereich messen, ermitteln sie demnach nicht die 'Lichtgeschwindigkeit' im 3-D, sondern die Geschwindigkeit der Raum-Matrixwellen im 4-D-Raum. Jedes einzelne Photon stellt dabei eine ruhende Verbindungsstrecke im 3-D dar. In diesem Modell besteht somit kein Widerspruch zwischen der Existenz der Photonen außerhalb der Zeit und auf der anderen Seite sichtbaren Veränderungen im 3-D.
Wenn Forscher Ortsveränderungen im Lichtbereich messen, ermitteln sie demnach nicht die 'Lichtgeschwindigkeit' im 3-D, sondern die Geschwindigkeit der Raum-Matrixwellen im 4-D-Raum. Jedes einzelne Photon stellt dabei eine ruhende Verbindungsstrecke im 3-D dar. In diesem Modell besteht somit kein Widerspruch zwischen der Existenz der Photonen außerhalb der Zeit und auf der anderen Seite sichtbaren Veränderungen im 3-D.
Auch für die Komplementäreigenschaften Licht/Welle des Photons ist das 4-D-Modell verwendbar und die Erscheinung eines Photons als Welle oder ein anderes Mal als Teilchen wird unmittelbar einleuchtend.

Die horizontale Ebene in Abb. 26 stellt den um eine Dimension reduzierten 3-D dar. Eine Lichtwelle welche im 4-D die 4-D-Punkte C und D verbindet, schneidet den 3-D in Z und erscheint dann dort als Teilchen. Die gleiche Welle kann aber auch die 4-D-Punkte A und B verbinden, die zudem im Schnitt mit dem 3-D liegen. In diesem Fall wird der Wellencharakter erkennbar. Welcher von den beiden Zuständen sich manifestiert, entscheidet die Vorrichtung. Jedes Photon wird bei der Messung vernichtet. Man kann es also nur einmal messen, entweder als 'Teilchen' oder als 'Welle'.
15. ROTVERSCHIEBUNG.
VESTO M. SLIPHER präsentierte 1914 der Tagung der Astronomischen Gesellschaft die ersten genauen Spektralanalysen von Sternen, wobei sich herausstellte, daß die Linien gegenüber denen im Labor hergestellten, stark verschoben waren. Dies wurde als 'DOPPLEReffekt' interpretiert und EDWIN HUBBLE veröffentlichte zwischen 1925 und 1929 die ersten Arbeiten darüber, wobei als Grundlage die Idee war, dass diese Verschiebung der Spektrallinien zum roten Bereich hin für ein expandierendes Universum sprach. "aber er akzeptierte nie völlig, daß die Rotverschiebung nur von der Radialgeschwindigkeit der Galaxien herrühren sollte."

Wenn man die Konsequenzen der Quantenphysik akzeptiert, stimmt das auch. Das Problem, welches das Wesen der Quantensprünge illustriert, ist der Übergang eines Elektrons von einer Schale der Atomhülle auf eine andere Schale. In Abb. 27a ist ein Übergang eines Elektrons von der K-Schale zur L-Schale skizziert. Dabei gibt es die überflüssige Energie in Form eines Photons ab.
Würden die klassischen Gesetze gelten, dann müßte zwischen dem Aufenthalt in L und der Ankunft in K eine Zeitunterschied zwischen den Zeitpunkten 1 und 2 nachweisbar sein, wie es die untere Kurve in Abb. 67b zeigt. Auf der unteren Achse ist der Abstand zwischen den Elektronenschalen K und L aufgetragen, nach oben die Zeit. Durch die Bewegung würde sich der Energiezustand ändern, der sich durch eine Verbreiterung der Spektrallinie der abgesendeten Photonen zeigen müßte. Dies ist aber nicht der Fall! Also muß der Wechsel der Bahnen in 'Nullzeit' stattfinden, was die obere Linie von Abb. 67b zeigt. "Diese scheinbar einfache Vorstellung bedeutete in Wirklichkeit einen tiefen Bruch mit den klassischen Vorstellungen. Es ist, als würde der Mars aus seiner Bahn verschwinden, unverzüglich in der Bahn der Erde wieder auftauchen und dabei einen Energiestrom ... in den Raum strahlen." Die abgestrahlte Energie ist dabei in feste Größen gepackt und wird sofort, ohne Zeitdifferenz abgegeben! "Man hätte solche Vorstellungen wohl nie ernst genommen, wenn man nicht damit eine ganze Reihe von Experimenten hätte sehr gut und genau erklären können."
Der DOPPLEReffekt
In Abb. 28 ist ein Objekt gegeben, welches sich in einem Medium z.B. Luft bewegt und dabei Schallwellen erzeugt. Wenn das Objekt ruht, breiten sich die Wellen konzentrisch in sphärischer Form aus. Wenn sich das Objekt dabei bewegt, entsteht zwischen der Eigenschwindigkeit des Objektes und der Geschwindigkeit der Schallwellen eine Differenz. Da Schallwellen aber Longitudinalwellen sind, addieren, bzw. subtrahieren sich die Geschwindigkeiten und ein Beobachter von vorne (3) nimmt eine höhere Frequenz war, als sie vom Objekt erzeugt wird. Dahinter (2) erscheint sie tiefer und nur ein seitlicher Beobachter (1) hört die ursprüngliche Frequenz. Ohne das Medium Luft verschwindet der DOPPLEReffekt sofort, da es dann auch keinen Schall mehr gibt. Wichtig ist auch die Schallaussendung in der Zeit und addier- bzw. subtrahierbare Geschwindigkeiten von Objekt und Wellenausbreitung. Beobachter 1 befindet sich rechtwinklig zum Geschehen, weshalb in diesem Zeitpunkt der Dopplereffekt für ihn nicht erfahrbar ist.

Nun wendet man das Ganze auf Licht an. Ende des 19. Jahrhunderts wurde noch über ein Trägermedium für Licht diskutiert, der sogenannte 'Äther', der heute für die Physiker das ist, was der Teufel für den Pfarrer darstellt (wer vom 'Äther' spricht, muß verrückt sein, und diese Besessenheit muß man der Person am besten austreiben). Da es aber nun kein Trägermedium für Licht geben darf, fällt der erste Punkt zur Erzeugung des Dopplereffekts weg.
Wenden wir uns dem nächsten Punkt zu, der Addition und Subtraktion von Geschwindigkeiten. Die Versuche von MICHELSON und MORLEY 1887 zeigten, daß bei einer angenommenen Geschwindigkeit von Licht diese immer gleich ist, egal in welcher relativen Geschwindigkeit man sich dazu bewegt! Anders ausgedrückt, sie ist unabhängig von irgend einem Bewegungszustand im 3-D. Damit ist es aber auch nicht erlaubt, die Geschwindigkeit des lichtaussendenden Objekts von der angeblichen Lichtgeschwindigkeit abzuziehen oder dazuzuzählen. Dies verletzt im Kern die Relativitätstheorie von EINSTEIN. Und wem das noch nicht reicht, der kann noch die Quantenphysik hinzuziehen.

Die Aussendung eines Gammaquants (Photons) erfolgt durch einen Quantensprung eines Elektrons der Atomhülle, in dem das gesamte Photon auf einmal abgeschickt wird (Abb. 29a). Dabei ist aber keine Frequenzänderung möglich, da diese eine Zeitdifferenz erfordert. Geht man aber von einer Verlängerung der Frequenz des Photons aufgrund der Eigengeschwindigkeit v des Objektes aus, so muß die Aussendung des Photons in einer endlichen Zeitdifferenz erfolgen, d.h. die Photonenwelle muß in der Zeit Schwingung für Schwingung das Objekt verlassen (Abb. 29b). Dies verletzt aber die Quantenbedingungen und im Experiment müßte man breite Spektrallinien sehen, was nicht der Fall ist.
Als viertes betrachten wir die Sache auf der mathematisch-physikalischen Ebene. Als Welle ist jedes einzelne Photon unendlich lang ausgedehnt, aber die Geschwindigkeit mit dem Wert 'Unendlich pro Sekunde' gibt es nicht. Das Photon verbindet in Wellenform einfach zwei Punkte im Raum miteinander. Photonen interagieren im freien Raum nie miteinander, sondern nur innerhalb eines Masseobjektes. Als Partikel hat das Photon die Energie im Drehimpuls gespeichert, wobei dieser Impuls genau der Frequenz des Photons proportional ist. Drehimpulse sind aber unabhängig von linearer Geschwindigkeit. Nimmt man in einem Auto einen schwarzen Kreisel mit und markiert den Rand mit einem weißen Strich, so können sowohl die Passagiere wie auch Passanten auf der Straße genau die Anzahl der Drehungen zählen. Die linearen Bewegungen ändern nichts am Drehimpuls des Kreisels.
Fazit: Die 'Theorie' über die Rotverschiebung auf Grund einer angeblichen 'Fluchtgeschwindigkeit' der Sterne ist in allen Aspekten falsch!
Der Astrophysiker JAMES TREFIL schreibt dazu: "Ich erinnerte mich an einen Imbiß in einem angesehenen physikalischen Institut, bei dem ein sehr prominentes Mitglied dieser Fakultät (ich würde es nicht wagen, ihn durch die Erwähnung seines Namens in Verlegenheit zu bringen) sagte, er spiele oft mit dem Gedanken, einen versiegelten Umschlag zu hinterlassen, der fünfzig Jahre nach seinem Tod geöffnet werden solle. Er enthielte seine Vorhersagen über die Ergebnisse bestimmter wissenschaftlicher Kontroversen. An erster Stelle der Liste, fuhr er fort, stünde die Vorhersage, die Interpretation der Rotverschiebung als Beweis für die Ausdehnung des Universums würde sich als falsch erweisen."
Kritik an der Rotverschiebung äußerte 1952 MAX BORN in einem Brief an ALBERT EINSTEIN , als er schrieb: "Es sieht wirklich so aus, als ob Deine Formel nicht ganz stimmt. Bei der Rotverschiebung sieht es noch schlimmer aus; im Inneren der Sonnenscheibe ist sie viel kleiner, am Rand größer als der theoretische Wert" .
Spektralverschiebung als Raumkrümmungseffekt
ERNST MACH erwähnt in einer Bemerkung, daß er bei der Überlegung für eine Erklärung der Linienspektren die Idee hatte, daß nichtsinnliche Dinge nicht notwendigerweise im sinnlich wahrnehmbaren dreidimensionalen Raum vorgestellt werden müssen: "So kam ich auf Analoga des Raumes von verschiedener Dimensionszahl" . Akzeptiert man höherdimensionale Räume als existent, so gibt es eine einfache Erklärung für vorhandene Rotverschiebung von Lichtspektren, die sogar unterschiedliche Verschiebungen bei Doppelsternen mit einschließt. Als Raummodell nehme ich die Konstruktion von Abb. 30 als Basis.
Da vierdimensionale Raumkonstruktionen nicht gerade üblich sind, werde ich zur Eingewöhnung ein Beispiel vorschalten, welches sich im einsehbaren 2-D abspielt.

Der gekrümmt 2-D hat, wie ich schon oben zeigte, die Form eines Torus im 3-D-Einbettungsraum. Projiziert man die Torusoberfläche auf den 2-D wie in Abb. 30a , so erhält man einen Kreis mit Mittelpunkt, wenn man einen Torus mit Lochdurchmesser Null gewählt hat, ansonsten ist es ein Kreisring. Im Querschnitt erzeugte der Torus im 2-D zwei getrennte Kreise. Die Projektion auf die Ebene ist aber doppelt, da die Ebene den Torus in zwei Hälften schneidet (siehe auch Abschnitt über Kodimension). Legt man auf dem Torus in gleichen Abständen Umfänge an, so erscheinen diese an den Rändern und zur Mitte der Kreisprojektion verdichtet (Abb. 30b). Würde man Volumenelemente des Torus auf den Kreis projizieren, hätten diese die umgekehrte Charakteristik, sie wären zur Mitte hin dichter als nach außen.
Bei der Projektion des 4-D-Hypertorus in dem dreidimensionalen Raum geschieht etwas ähnliches. Der Hypertorus erscheint im 3-D als Kugel mit Mittelpunkt wie in Abb. 30a. Eine einzige Ebene der Hypertorus, wie in Abb. 30b, entspricht in der 3-D-Projektion schon einer ganzen Kugel! Eine analoge Erscheinung hätte man im 2-D. Zweidimensionale Wesen würden ein Kugel als 'Hyperkreis' bezeichnen, wobei ein einziger Kugelschnitt schon einen kompletten Kreis ausfüllt, aber damit hätte man die Kugel genausowenig umfassend beschrieben, wie im vierdimensionalen Fall mit der Kugel den Hypertorus. Der senkrechte Schnitt in Abb. 31a ist ebenfalls ein gültiger Teil des Hypertorus. Die Durchdringung mit der horizontalen Projektion ist nur scheinbar, denn in der 4-D-Wirklichkeit sind sie getrennt.

Wenn nun Licht, wie oben gezeigt wurde, eine Erscheinung des 4-D ist, dann ist die Ausbreitung der Photonen nicht an den 3-D gebunden und sie können auch von außen in den von uns sichtbaren Raum eindringen. Dabei müssen sie sich der Raummatrix anpassen und erfahren eine Wellenlängenänderung, die in Abb. 32 skizziert ist.

Auf der linken Seite sollen sich im gekrümmten 3-D an einer weit entfernten Stelle Doppelsterne oder Quasare befinden. Vom lokalen Beobachter aus kann die Entfernung täuschen, da die Lichtquelle im gleichen Raumsektor 'nah' erscheinen mag. Dies kann aber ein Effekt des gekrümmten Raumes sein, so wie in Abb. 31 auf dem Torus weit auseinanderliegende Punkte in der Projektion nahe beieinander zu liegen scheinen. Indem das Licht die 'Abkürzung' durch den 4-D nimmt, hat es einen gewissen Winkel beim Wiedereintritt in den 3-D und muß sich dort der Raumstruktur anpassen. Um sich nicht von der Skizze irreführen zu lassen, muß man sich daran erinnern, daß vom 4-D aus der 3-D komplett offen vor einem liegt. Man kann dann auch z.B. von innen in Objekte einsehen.
In Abb. 32b sieht man, daß die Wellenlänge des Lichts beim durchkreuzen des 3-D eine Verlängerung erfährt, da die ursprüngliche Länge einer Kathede und der Abstand im 3-D der Hypothenuse eines rechtwinkligen Dreiecks entspricht. Bei gleicher Kathede verlängert sich die Hypothenuse mit zunehmendem Einfallswinkel vom 4-D. Je paralleler der Winkel, um so weniger geht die Wellenlängenverschiebung zum roten Bereich. Bei diesem Modell des Universums ist es notwendig, daß Doppelsterne, die im Bezug zu einem bestimmten Beobachter unterschiedliche Winkel aufweisen, unterschiedliche Rotverschiebung haben. Damit könnte man die Daten von verschiedenen Quasaren erklären.
Aber dieser Effekt könnte auch innerhalb des 3-D-Raumes auftreten, wenn nämlich durch große Masseanhäufungen der Raum in sich gekrümmt ist. Zwar ist innerhalb des 3-D diese Krümmung nicht direkt erfahrbar, aber von einem Beobachter außerhalb des 3-D würde dies durch eine Verdichtung der Raummatrix erkennbar sein. Da Photonen aber 4-D-Erscheinungen sind, treffen sie dann vom 4-D aus in einem Winkel zur 3-D-Raummatrix am Beobachtungsort ein und erfahren dort in gleicher Weise wie in Abb. 32 eine Verlängerung der Wellenlänge.
Mit diesem Modell könnte man die Eigenschaften des Quasars 3 C 279 als Zweikomponentensystem erklären, über die P.STUBBS berichtete , dessen beiden Komponenten sich angeblich ‘auseinanderbewegen’. Wenn man die Rotverschiebung als Fluchtgeschwindigkeit interpretiert, kommt man auf das zehnfache der 'Lichtgeschwindigkeit'. Ebenfalls hätte man Erklärungen für die von HALTON ARP gefundenen Galaxienpaare, deren Teile aufgrund der bisher geltenden Theorien unterschiedliche Geschwindigkeiten haben müßten, die sich um das zehnfache unterscheiden. Das ist, als würde man behaupten, bei einem Fahrrad würde das Vorderrad sich mit 10 km/h und das Hinterrad mit 100 km/h bewegen. In 16 Fällen fand ARP bei jüngeren Tochtergalaxien eine höhere Rotverschiebung als bei den älteren Muttergaklaxien. Die erste Reaktion der Astronomen war, daß sie diese Beobachtung als 'optische Täuschung' bezeichneten. "Der Widerstand der Astronomen, ihre Beobachtungszeit auf die Verfolgung der Gedanken Arps zu verwenden, ist vielleicht analog zu der Abneigung zu sehen, die fast alle Wissenschaftler gegen den ‘siebten Sinn', die außersinnliche Wahrnehmung, hegen."
16. LICHTBRECHUNG IN DURCHSICHTIGEN OBJEKTEN
In den Physikbüchern steht, daß in durchsichtigen Körpern die 'Lichtgeschwindigkeit' c eine Funktion der Frequenz sei. Die daraus folgende Abhängigkeit der Brechzahl n eines Körpers von der Frequenz nennt man Dispersion. Die unterschiedlichen 'Geschwindigkeiten' des Lichts im Glas seien angeblich auch für die Brechung (Abb. 33a) verantwortlich. Läßt man einmal den Punkt beiseite, daß die Photonen keine Geschwindigkeit haben, so ergibt sich ein weiterer Widerspruch mit der Erklärung des Verhaltens von Licht an einer planparalleln Platte (Abb. 33b). Hier, so heißt es, werde das Licht nur parallel verschoben, gehe aber ansonsten unverändert durch. Den Widerspruch erkennt man durch zwei aneinandergelegte Prismen (Abb. 33c).
Diese zwei Prismen ergeben eine planparallele Platte, also dürfte sich das Licht nicht aufspalten. Da es aber Prismen sind, müßte die Aufspaltung trotzdem stattfinden. Und, was interessant ist, das Licht müßte am Anfang beim Eintreten schon 'wissen', welchen Winkel die andere Glasseite hat, um sich zu entscheiden ob der Strahl aufgespalten wird oder nicht. Nun könnte man kommen und sagen, die Aufspaltung finde zwar immer statt, aber der Effekt sei so klein, daß man ihn vernachlässigen könne. Das stimmt leider nicht. Bei Flintglas, das einen großen Dispersionsindex hat, müßte man den Effekt bei nur 1 cm dicken Glas schon mit bloßem Auge sehen, denn die Aufspaltung müßte ca 1/10 Millimeter sein (!), etwa in der Größenordnung der Breite eines Millimeterstrichs auf einem Meßband.

Ein weiteres Beispiel dazu: wenn die Aussage über verschiedene Brechungswinkel wegen unterschiedlicher Geschwindigkeiten stimmen würde, dann müßten sich in einem langen Glasfaserkabel bei jeder Reflexion an der Glaswand die roten und violetten Strahlen voneinander entfernen. Aus einem kompakten Strahl am Anfang des Glaskabels müßte dann am Ende ein breites Regenbogenspektrum werden.
Auf gleicher Ebene befindet sich das Problem der partiellen Reflexion an einer Glasoberfläche. Läßt man 100 Photonen auf eine Glasoberfläche los, dann gehen 96 durch und vier kommen zurück. "Und damit fangen unsere Schwierigkeiten bereits an: Wie ist es überhaupt möglich, daß Licht nur teilweise reflektiert wird? Das eine Photon landet in A, das andere in B - wie 'entscheidet' es sich, wohin es will?" RICHARD FEYNMAN schreibt, daß seine Zuhörer auf diese Bemerkung hin lachten. Er meinte, daß es wie ein Witz klingen mag, aber mit Lachen sei es nicht getan. Hier hat man es mit einem Beispiel zu tun, wo eine gleiche Voraussetzung zu unterschiedliche Resultaten führt. Bei einem einzelnen Photon läßt es sich nicht voraussagen, ob es durch das Glas geht, oder ob es reflektiert wird. Und trotzdem sind am Ende bei hundert Photonen 96 durchgelassen worden und 4 kamen zurück. Die Frage ist nun, woher weiß das fünfzigste Photon, ob es das fünfzigste ist oder das erste oder das hundertste, um entweder durchzugehen oder nicht, damit am Ende die Statistik der Forscher stimmt? Da Photonen ihre eigenen Antiteilchen sind, muß man jede Verbindung die sie herstellen, von beiden Seiten betrachten können. Offensichtlich muß die Frage anders gestellt werden.

Mit der Annahme eines 4-D-Raumes und der zugehörigen Matrixschwingung des uns zugänglichen 3-D in Richtung 4-D, gibt es einen Weg aus dem Problem. Die weitere Voraussetzung ist ein Quantenverhalten des Systems. Ein Stück Masse, in diesem Fall Glas, ist den permanenten 4-D-Matrix-Schwingungen des Raumes ausgesetzt, wobei sich die Atomstruktur diesen Bewegungen anpassen muß. Aufgrund innerer Masseverhältnisse und Quantenverhalten wird bevorzugt ein Zustand eingenommen, bei dem die Materiewellen an der Oberfläche Knoten haben. Dies entspricht einer schwingenden Gitarresaite (Abb. 34a). Kurzzeitig wird allerdings der Energiebetrag zur Aufrechterhaltung dieser Frequenz über- oder unterschritten, und eine neue Quantenschwingung stellt sich ein, deren Länge aber inkompatibel mit der Distanz der Brechungsflächen ist. Dadurch sind keine Knoten an der Oberfläche, sondern Schwingungsbäuche, welche den Durchgang von Photonen verhindern (Abb. 34b), ähnlich wie ein drehender Ventilator Objekte zurückwirft.
Man könnte den Prozeß auch mit einem Klavier vergleichen. Setzt man als Analogie für die Durchgangsbedingungen die Oktaven einer Frequenz, z.B. das 'c', dann wird die Passage gesperrt, wenn bei einer der Oktaven aus dem 'c' ein 'h' oder 'cis' wird. In dieses Modell paßt auch die Erfahrung aus der Optik, daß dünne aufgedampfte Metallschichten den Durchgang einer bestimmten Frequenz ermöglichen, den von anderen jedoch blockieren. Wenn die Schichtdicke der Wellenlänge entspricht, schwingt der Raum an der Stelle mit Knoten an den Endflächen und ermöglicht den Photonen den Durchgang.

Sind die Endflächen zueinander geneigt, wie beim Prisma, dann sind von jedem Eintrittspunkt des Glases aus, den unterschiedlichen Längen der Wellen entsprechend, quantisierte Strecken zum Austritt möglich, die sich fächerförmig aufspalten (Abb 35). Bei einer planparallelen Platte ist dies nicht möglich, da hier die Raummatrix parallel schwingt.
Das Brechungsgesetz muß dann neuformuliert so heißen: Die Raummatrix in festen (flüssigen, gasförmigen ) Objekten schwingt langsamer als im Vakuum. Liegt innerhalb eines Lichtstrahls ein durchsichtiger Körper, so verkürzt dieser durch die von ihm verursachte Raumkrümmung den Abstand zwischen Lichtquelle und Auftreffpunkt. Die Verbindung des Lichtstrahls von der Quelle zum Objekt erfolgt zu Zeitpunkten, an denen die Raummatrix an der Oberfläche des durchsichtigen Körpers Knoten hat. Ist dort ein Schwingungsbauch, wird das auftreffende Photon reflektiert und folgt der Struktur der äußeren Raummatrix. Die Wellenlänge innerhalb des durchsichtigen Körpers hängt vom Material ab. Der Prozentsatz an reflektierten Photonen hängt vom Prozentsatz der Zeit ab, in welcher der Raum an der Grenzfläche Schwingungsbäuche statt Schwingungsknoten hat.
-
nicole6

- ModeratorIn

- Beiträge: 2333
- Registriert: 11.09.2009, 13:01
- Wohnort: München
- Ich bin: ehemalige SexarbeiterIn
RE: Diskussionspapier: Modell für Zeit und Raum
13. PHOTONEN.
Es besteht eine große Verwirrung in der synonymen Verwendung der Begriffe 'Licht' und 'Photonen'. Ein Photon ist ein einzelnes und quantisiertes Energiepartikel. Seine Energie ist durch einen einzigen Parameter gegeben: die Frequenz. Es ist elektrisch neutral, ohne Masse und hat den Spin 1, d.h. im hier vorgestellten Modell des Torus ist das Verhältnis der Drehungen um beide Torusachsen L und R 1:1.
Von der Regel, daß jedes Teilchen sein separates Antiteilchen hat, macht das Photon eine Ausnahme, denn es ist sein eigenes Antiteilchen. Die daraus folgenden Konsequenzen wurden bisher von wenigen Forschern beachtet. Teilchen und Antiteilchen unterscheiden sich durch die Zeitrichtung. Ein Teilchen wie das Photon, das beide Zeitrichtungen umfaßt, hat logischerweise im 3-D keine Geschwindigkeit: " Zum Beispiel, wir hören manchmal die Aussage, daß ein Lichtsignal von einem Teil der Raumzeit zu einem anderen abgesendet wurde. Die korrekte Ausdrucksweise für diesen Sachverhalt ist zu sagen, daß das Lichtsignal (spannungslos) entlang einer Linie zwischen diesen beiden Teilen der Raumzeit liegt." MICHAEL SHALLIS formuliert es so: “Wenn sich die Zeit in Annäherung an die Lichtgeschwindigkeit verlangsamt, kann man davon ableiten, daß für ein Photon, ein Lichtpartikel, Zeit nicht existiert. Zu diesem Ausmaß kann ein Photon rund um das Universum in Null-Zeit reisen, weil es in seinen Referenzrahmen keine Zeit gibt.”
Photonen sind quantisiert. Der Übertragungsmechanismus dieser Quanten ist aber noch sehr unklar. "Wenn Begriffe nicht anschaulich sind, sind sie noch nicht geklärt. In der Quantenoptik sind sie nicht anschaulich, also sind sie noch nicht geklärt" .
Photonen interagieren nicht miteinander! Ansonsten könnten wir nichts sehen, da sich die Photonen gegenseitig vernichten würden. In einem Raum können sie ungestört jeden Punkt des Raumes mit jedem anderen verbinden. Interaktion, d.h. Interferenz geschieht nicht mit anderen Photonen, sondern mit Masse-besetzten Objekten. Wenn die Zahl der einzelnen Photonen auf einer Brom-Silberschicht energetisch ausreicht das Brom vom Silber zu trennen, wird das Silber frei und wenn man das Brom abwäscht, wird ein schwarzer Silberpunkt sichtbar. Wenn nicht, bleibt die Stelle weiß. Aber untereinander gibt es keine Interferenz.
Der Begriff 'Licht' wird allgemein im Sinn verwendet, daß eine große Zahl von Photonen am Prozeß beteiligt sind, von denen jedes einzelne keine Geschwindigkeit hat und keines mit irgend einem anderen interagiert. "Eine gewöhnliche Glühbirne emittiert in einer milliardstel Sekunde mehr als 100 Milliarden von ihnen." Wenn aber die Geschwindigkeit eines Photons Null ist, dann ist die von einer Billion Photonen ebenfalls Null, denn eine Billion mal Null ist und bleibt Null.
14. 'LICHTGESCHWINDIGKEIT'.
Wie konnte es aber zum Begriff 'Lichtgeschwindigkeit' kommen? Ein Grund ist sicher der, daß die Forscher durch jahrhundertelange Rezeption griechischer Philosophen so hypnotisiert waren, daß sie zwangsläufig ‘Zeit’ und ‘Werden’ mit 'Geschwindigkeit' verbanden. Das krampfhafte Festhalten an der Vorstellung des dreidimensionalen Raumes als Existenzgrundlage tat das übrige dazu. So sahen sie Geschwindigkeiten, wo nur Veränderungen waren und ignorierten geflissentlich Beweise, die auf höherdimensionale Räume hinwiesen. Probleme gab es schon früh, als 1887 ALBERT MICHELSON und EDWARD MORLEY versuchten die 'Lichtgeschwindigkeit' zu messen. Zu ihrer Überraschung waren die 'Geschwindigkeiten' immer gleich, egal in welchem relativen Bewegungszustand man sich zur Lichtquelle befand.
Um das Problem einsichtig zu machen, reduziert man die Dimensionen um eine und betrachtet ein zweidimensionales Geschehen im 2-D. Die Ereignisse im 2-D-Land seien auf einem Film festgehalten, welche einsichtige Wesen im 3-D im Kino anschauen. Der Film im Projektor soll beispielsweise 30 Bilder pro Sekunde vorrücken und die Projektion auf der Leinwand habe 10 Meter Durchmesser. Offensichtlich verändern sich die Dinge im 2-D-Universum und die Wissenschaftler auf der Leinwand bemühen sich nun, die Geschwindigkeit von Lichtstrahlen zwischen zwei Punkten zu messen. Aber egal wie sie messen, die 'Geschwindigkeit' ist immer die Gleiche, sie ist 300 Meter pro Sekunde, egal in welche Richtung sie sich in ihrem 2-D bewegen. Und was sie noch feststellen, diese 300 m/sec sind eine Art 'Grenzgeschwindigkeit', die nicht zu übertreten ist. In ihrem 2-D kann kein Signal von einem Punkt der Leinwand früher zu einem anderen Punkt kommen als nach 1/30 Sekunde (Abbildung 25).
Vom 3-D aus wird der Sachverhalt jedoch klar und ist nicht mehr mysteriös. Wenn eine Person beispielsweise einen Stern erblickt, dann verbindet ein Photon den Stern und das Auge für diesen Augen-Blick. Es gibt keine wirkliche Bewegung der Zeit, in der sich eine Bahn von dem Stern bis zu meinem Auge entwickelt; das ist nur meine Wahrnehmung von meinem Standpunkt aus. Von einem anderen, ebenso gültigen Standpunkt aus ist die Bahn eine ewige Erscheinung, um die herum das Universum sich verändert, und im Laufe dieser Veränderungen im Universum kommt es unter anderem dazu, daß sich mein Auge und der Polarstern zufällig an den entgegengesetzten Enden der Bahn befinden."

Wenn Forscher Ortsveränderungen im Lichtbereich messen, ermitteln sie demnach nicht die 'Lichtgeschwindigkeit' im 3-D, sondern die Geschwindigkeit der Raum-Matrixwellen im 4-D-Raum. Jedes einzelne Photon stellt dabei eine ruhende Verbindungsstrecke im 3-D dar. In diesem Modell besteht somit kein Widerspruch zwischen der Existenz der Photonen außerhalb der Zeit und auf der anderen Seite sichtbaren Veränderungen im 3-D.
Wenn Forscher Ortsveränderungen im Lichtbereich messen, ermitteln sie demnach nicht die 'Lichtgeschwindigkeit' im 3-D, sondern die Geschwindigkeit der Raum-Matrixwellen im 4-D-Raum. Jedes einzelne Photon stellt dabei eine ruhende Verbindungsstrecke im 3-D dar. In diesem Modell besteht somit kein Widerspruch zwischen der Existenz der Photonen außerhalb der Zeit und auf der anderen Seite sichtbaren Veränderungen im 3-D.
Auch für die Komplementäreigenschaften Licht/Welle des Photons ist das 4-D-Modell verwendbar und die Erscheinung eines Photons als Welle oder ein anderes Mal als Teilchen wird unmittelbar einleuchtend.

Die horizontale Ebene in Abb. 26 stellt den um eine Dimension reduzierten 3-D dar. Eine Lichtwelle welche im 4-D die 4-D-Punkte C und D verbindet, schneidet den 3-D in Z und erscheint dann dort als Teilchen. Die gleiche Welle kann aber auch die 4-D-Punkte A und B verbinden, die zudem im Schnitt mit dem 3-D liegen. In diesem Fall wird der Wellencharakter erkennbar. Welcher von den beiden Zuständen sich manifestiert, entscheidet die Vorrichtung. Jedes Photon wird bei der Messung vernichtet. Man kann es also nur einmal messen, entweder als 'Teilchen' oder als 'Welle'.
15. ROTVERSCHIEBUNG.
VESTO M. SLIPHER präsentierte 1914 der Tagung der Astronomischen Gesellschaft die ersten genauen Spektralanalysen von Sternen, wobei sich herausstellte, daß die Linien gegenüber denen im Labor hergestellten, stark verschoben waren. Dies wurde als 'DOPPLEReffekt' interpretiert und EDWIN HUBBLE veröffentlichte zwischen 1925 und 1929 die ersten Arbeiten darüber, wobei als Grundlage die Idee war, dass diese Verschiebung der Spektrallinien zum roten Bereich hin für ein expandierendes Universum sprach. "aber er akzeptierte nie völlig, daß die Rotverschiebung nur von der Radialgeschwindigkeit der Galaxien herrühren sollte."

Wenn man die Konsequenzen der Quantenphysik akzeptiert, stimmt das auch. Das Problem, welches das Wesen der Quantensprünge illustriert, ist der Übergang eines Elektrons von einer Schale der Atomhülle auf eine andere Schale. In Abb. 27a ist ein Übergang eines Elektrons von der K-Schale zur L-Schale skizziert. Dabei gibt es die überflüssige Energie in Form eines Photons ab.
Würden die klassischen Gesetze gelten, dann müßte zwischen dem Aufenthalt in L und der Ankunft in K eine Zeitunterschied zwischen den Zeitpunkten 1 und 2 nachweisbar sein, wie es die untere Kurve in Abb. 67b zeigt. Auf der unteren Achse ist der Abstand zwischen den Elektronenschalen K und L aufgetragen, nach oben die Zeit. Durch die Bewegung würde sich der Energiezustand ändern, der sich durch eine Verbreiterung der Spektrallinie der abgesendeten Photonen zeigen müßte. Dies ist aber nicht der Fall! Also muß der Wechsel der Bahnen in 'Nullzeit' stattfinden, was die obere Linie von Abb. 67b zeigt. "Diese scheinbar einfache Vorstellung bedeutete in Wirklichkeit einen tiefen Bruch mit den klassischen Vorstellungen. Es ist, als würde der Mars aus seiner Bahn verschwinden, unverzüglich in der Bahn der Erde wieder auftauchen und dabei einen Energiestrom ... in den Raum strahlen." Die abgestrahlte Energie ist dabei in feste Größen gepackt und wird sofort, ohne Zeitdifferenz abgegeben! "Man hätte solche Vorstellungen wohl nie ernst genommen, wenn man nicht damit eine ganze Reihe von Experimenten hätte sehr gut und genau erklären können."
Der DOPPLEReffekt
In Abb. 28 ist ein Objekt gegeben, welches sich in einem Medium z.B. Luft bewegt und dabei Schallwellen erzeugt. Wenn das Objekt ruht, breiten sich die Wellen konzentrisch in sphärischer Form aus. Wenn sich das Objekt dabei bewegt, entsteht zwischen der Eigenschwindigkeit des Objektes und der Geschwindigkeit der Schallwellen eine Differenz. Da Schallwellen aber Longitudinalwellen sind, addieren, bzw. subtrahieren sich die Geschwindigkeiten und ein Beobachter von vorne (3) nimmt eine höhere Frequenz war, als sie vom Objekt erzeugt wird. Dahinter (2) erscheint sie tiefer und nur ein seitlicher Beobachter (1) hört die ursprüngliche Frequenz. Ohne das Medium Luft verschwindet der DOPPLEReffekt sofort, da es dann auch keinen Schall mehr gibt. Wichtig ist auch die Schallaussendung in der Zeit und addier- bzw. subtrahierbare Geschwindigkeiten von Objekt und Wellenausbreitung. Beobachter 1 befindet sich rechtwinklig zum Geschehen, weshalb in diesem Zeitpunkt der Dopplereffekt für ihn nicht erfahrbar ist.

Nun wendet man das Ganze auf Licht an. Ende des 19. Jahrhunderts wurde noch über ein Trägermedium für Licht diskutiert, der sogenannte 'Äther', der heute für die Physiker das ist, was der Teufel für den Pfarrer darstellt (wer vom 'Äther' spricht, muß verrückt sein, und diese Besessenheit muß man der Person am besten austreiben). Da es aber nun kein Trägermedium für Licht geben darf, fällt der erste Punkt zur Erzeugung des Dopplereffekts weg.
Wenden wir uns dem nächsten Punkt zu, der Addition und Subtraktion von Geschwindigkeiten. Die Versuche von MICHELSON und MORLEY 1887 zeigten, daß bei einer angenommenen Geschwindigkeit von Licht diese immer gleich ist, egal in welcher relativen Geschwindigkeit man sich dazu bewegt! Anders ausgedrückt, sie ist unabhängig von irgend einem Bewegungszustand im 3-D. Damit ist es aber auch nicht erlaubt, die Geschwindigkeit des lichtaussendenden Objekts von der angeblichen Lichtgeschwindigkeit abzuziehen oder dazuzuzählen. Dies verletzt im Kern die Relativitätstheorie von EINSTEIN. Und wem das noch nicht reicht, der kann noch die Quantenphysik hinzuziehen.

Die Aussendung eines Gammaquants (Photons) erfolgt durch einen Quantensprung eines Elektrons der Atomhülle, in dem das gesamte Photon auf einmal abgeschickt wird (Abb. 29a). Dabei ist aber keine Frequenzänderung möglich, da diese eine Zeitdifferenz erfordert. Geht man aber von einer Verlängerung der Frequenz des Photons aufgrund der Eigengeschwindigkeit v des Objektes aus, so muß die Aussendung des Photons in einer endlichen Zeitdifferenz erfolgen, d.h. die Photonenwelle muß in der Zeit Schwingung für Schwingung das Objekt verlassen (Abb. 29b). Dies verletzt aber die Quantenbedingungen und im Experiment müßte man breite Spektrallinien sehen, was nicht der Fall ist.
Als viertes betrachten wir die Sache auf der mathematisch-physikalischen Ebene. Als Welle ist jedes einzelne Photon unendlich lang ausgedehnt, aber die Geschwindigkeit mit dem Wert 'Unendlich pro Sekunde' gibt es nicht. Das Photon verbindet in Wellenform einfach zwei Punkte im Raum miteinander. Photonen interagieren im freien Raum nie miteinander, sondern nur innerhalb eines Masseobjektes. Als Partikel hat das Photon die Energie im Drehimpuls gespeichert, wobei dieser Impuls genau der Frequenz des Photons proportional ist. Drehimpulse sind aber unabhängig von linearer Geschwindigkeit. Nimmt man in einem Auto einen schwarzen Kreisel mit und markiert den Rand mit einem weißen Strich, so können sowohl die Passagiere wie auch Passanten auf der Straße genau die Anzahl der Drehungen zählen. Die linearen Bewegungen ändern nichts am Drehimpuls des Kreisels.
Fazit: Die 'Theorie' über die Rotverschiebung auf Grund einer angeblichen 'Fluchtgeschwindigkeit' der Sterne ist in allen Aspekten falsch!
Der Astrophysiker JAMES TREFIL schreibt dazu: "Ich erinnerte mich an einen Imbiß in einem angesehenen physikalischen Institut, bei dem ein sehr prominentes Mitglied dieser Fakultät (ich würde es nicht wagen, ihn durch die Erwähnung seines Namens in Verlegenheit zu bringen) sagte, er spiele oft mit dem Gedanken, einen versiegelten Umschlag zu hinterlassen, der fünfzig Jahre nach seinem Tod geöffnet werden solle. Er enthielte seine Vorhersagen über die Ergebnisse bestimmter wissenschaftlicher Kontroversen. An erster Stelle der Liste, fuhr er fort, stünde die Vorhersage, die Interpretation der Rotverschiebung als Beweis für die Ausdehnung des Universums würde sich als falsch erweisen."
Kritik an der Rotverschiebung äußerte 1952 MAX BORN in einem Brief an ALBERT EINSTEIN , als er schrieb: "Es sieht wirklich so aus, als ob Deine Formel nicht ganz stimmt. Bei der Rotverschiebung sieht es noch schlimmer aus; im Inneren der Sonnenscheibe ist sie viel kleiner, am Rand größer als der theoretische Wert" .
Spektralverschiebung als Raumkrümmungseffekt
ERNST MACH erwähnt in einer Bemerkung, daß er bei der Überlegung für eine Erklärung der Linienspektren die Idee hatte, daß nichtsinnliche Dinge nicht notwendigerweise im sinnlich wahrnehmbaren dreidimensionalen Raum vorgestellt werden müssen: "So kam ich auf Analoga des Raumes von verschiedener Dimensionszahl" . Akzeptiert man höherdimensionale Räume als existent, so gibt es eine einfache Erklärung für vorhandene Rotverschiebung von Lichtspektren, die sogar unterschiedliche Verschiebungen bei Doppelsternen mit einschließt. Als Raummodell nehme ich die Konstruktion von Abb. 30 als Basis.
Da vierdimensionale Raumkonstruktionen nicht gerade üblich sind, werde ich zur Eingewöhnung ein Beispiel vorschalten, welches sich im einsehbaren 2-D abspielt.

Der gekrümmt 2-D hat, wie ich schon oben zeigte, die Form eines Torus im 3-D-Einbettungsraum. Projiziert man die Torusoberfläche auf den 2-D wie in Abb. 30a , so erhält man einen Kreis mit Mittelpunkt, wenn man einen Torus mit Lochdurchmesser Null gewählt hat, ansonsten ist es ein Kreisring. Im Querschnitt erzeugte der Torus im 2-D zwei getrennte Kreise. Die Projektion auf die Ebene ist aber doppelt, da die Ebene den Torus in zwei Hälften schneidet (siehe auch Abschnitt über Kodimension). Legt man auf dem Torus in gleichen Abständen Umfänge an, so erscheinen diese an den Rändern und zur Mitte der Kreisprojektion verdichtet (Abb. 30b). Würde man Volumenelemente des Torus auf den Kreis projizieren, hätten diese die umgekehrte Charakteristik, sie wären zur Mitte hin dichter als nach außen.
Bei der Projektion des 4-D-Hypertorus in dem dreidimensionalen Raum geschieht etwas ähnliches. Der Hypertorus erscheint im 3-D als Kugel mit Mittelpunkt wie in Abb. 30a. Eine einzige Ebene der Hypertorus, wie in Abb. 30b, entspricht in der 3-D-Projektion schon einer ganzen Kugel! Eine analoge Erscheinung hätte man im 2-D. Zweidimensionale Wesen würden ein Kugel als 'Hyperkreis' bezeichnen, wobei ein einziger Kugelschnitt schon einen kompletten Kreis ausfüllt, aber damit hätte man die Kugel genausowenig umfassend beschrieben, wie im vierdimensionalen Fall mit der Kugel den Hypertorus. Der senkrechte Schnitt in Abb. 31a ist ebenfalls ein gültiger Teil des Hypertorus. Die Durchdringung mit der horizontalen Projektion ist nur scheinbar, denn in der 4-D-Wirklichkeit sind sie getrennt.

Wenn nun Licht, wie oben gezeigt wurde, eine Erscheinung des 4-D ist, dann ist die Ausbreitung der Photonen nicht an den 3-D gebunden und sie können auch von außen in den von uns sichtbaren Raum eindringen. Dabei müssen sie sich der Raummatrix anpassen und erfahren eine Wellenlängenänderung, die in Abb. 32 skizziert ist.

Auf der linken Seite sollen sich im gekrümmten 3-D an einer weit entfernten Stelle Doppelsterne oder Quasare befinden. Vom lokalen Beobachter aus kann die Entfernung täuschen, da die Lichtquelle im gleichen Raumsektor 'nah' erscheinen mag. Dies kann aber ein Effekt des gekrümmten Raumes sein, so wie in Abb. 31 auf dem Torus weit auseinanderliegende Punkte in der Projektion nahe beieinander zu liegen scheinen. Indem das Licht die 'Abkürzung' durch den 4-D nimmt, hat es einen gewissen Winkel beim Wiedereintritt in den 3-D und muß sich dort der Raumstruktur anpassen. Um sich nicht von der Skizze irreführen zu lassen, muß man sich daran erinnern, daß vom 4-D aus der 3-D komplett offen vor einem liegt. Man kann dann auch z.B. von innen in Objekte einsehen.
In Abb. 32b sieht man, daß die Wellenlänge des Lichts beim durchkreuzen des 3-D eine Verlängerung erfährt, da die ursprüngliche Länge einer Kathede und der Abstand im 3-D der Hypothenuse eines rechtwinkligen Dreiecks entspricht. Bei gleicher Kathede verlängert sich die Hypothenuse mit zunehmendem Einfallswinkel vom 4-D. Je paralleler der Winkel, um so weniger geht die Wellenlängenverschiebung zum roten Bereich. Bei diesem Modell des Universums ist es notwendig, daß Doppelsterne, die im Bezug zu einem bestimmten Beobachter unterschiedliche Winkel aufweisen, unterschiedliche Rotverschiebung haben. Damit könnte man die Daten von verschiedenen Quasaren erklären.
Aber dieser Effekt könnte auch innerhalb des 3-D-Raumes auftreten, wenn nämlich durch große Masseanhäufungen der Raum in sich gekrümmt ist. Zwar ist innerhalb des 3-D diese Krümmung nicht direkt erfahrbar, aber von einem Beobachter außerhalb des 3-D würde dies durch eine Verdichtung der Raummatrix erkennbar sein. Da Photonen aber 4-D-Erscheinungen sind, treffen sie dann vom 4-D aus in einem Winkel zur 3-D-Raummatrix am Beobachtungsort ein und erfahren dort in gleicher Weise wie in Abb. 32 eine Verlängerung der Wellenlänge.
Mit diesem Modell könnte man die Eigenschaften des Quasars 3 C 279 als Zweikomponentensystem erklären, über die P.STUBBS berichtete , dessen beiden Komponenten sich angeblich ‘auseinanderbewegen’. Wenn man die Rotverschiebung als Fluchtgeschwindigkeit interpretiert, kommt man auf das zehnfache der 'Lichtgeschwindigkeit'. Ebenfalls hätte man Erklärungen für die von HALTON ARP gefundenen Galaxienpaare, deren Teile aufgrund der bisher geltenden Theorien unterschiedliche Geschwindigkeiten haben müßten, die sich um das zehnfache unterscheiden. Das ist, als würde man behaupten, bei einem Fahrrad würde das Vorderrad sich mit 10 km/h und das Hinterrad mit 100 km/h bewegen. In 16 Fällen fand ARP bei jüngeren Tochtergalaxien eine höhere Rotverschiebung als bei den älteren Muttergaklaxien. Die erste Reaktion der Astronomen war, daß sie diese Beobachtung als 'optische Täuschung' bezeichneten. "Der Widerstand der Astronomen, ihre Beobachtungszeit auf die Verfolgung der Gedanken Arps zu verwenden, ist vielleicht analog zu der Abneigung zu sehen, die fast alle Wissenschaftler gegen den ‘siebten Sinn', die außersinnliche Wahrnehmung, hegen."
16. LICHTBRECHUNG IN DURCHSICHTIGEN OBJEKTEN
In den Physikbüchern steht, daß in durchsichtigen Körpern die 'Lichtgeschwindigkeit' c eine Funktion der Frequenz sei. Die daraus folgende Abhängigkeit der Brechzahl n eines Körpers von der Frequenz nennt man Dispersion. Die unterschiedlichen 'Geschwindigkeiten' des Lichts im Glas seien angeblich auch für die Brechung (Abb. 33a) verantwortlich. Läßt man einmal den Punkt beiseite, daß die Photonen keine Geschwindigkeit haben, so ergibt sich ein weiterer Widerspruch mit der Erklärung des Verhaltens von Licht an einer planparalleln Platte (Abb. 33b). Hier, so heißt es, werde das Licht nur parallel verschoben, gehe aber ansonsten unverändert durch. Den Widerspruch erkennt man durch zwei aneinandergelegte Prismen (Abb. 33c).
Diese zwei Prismen ergeben eine planparallele Platte, also dürfte sich das Licht nicht aufspalten. Da es aber Prismen sind, müßte die Aufspaltung trotzdem stattfinden. Und, was interessant ist, das Licht müßte am Anfang beim Eintreten schon 'wissen', welchen Winkel die andere Glasseite hat, um sich zu entscheiden ob der Strahl aufgespalten wird oder nicht. Nun könnte man kommen und sagen, die Aufspaltung finde zwar immer statt, aber der Effekt sei so klein, daß man ihn vernachlässigen könne. Das stimmt leider nicht. Bei Flintglas, das einen großen Dispersionsindex hat, müßte man den Effekt bei nur 1 cm dicken Glas schon mit bloßem Auge sehen, denn die Aufspaltung müßte ca 1/10 Millimeter sein (!), etwa in der Größenordnung der Breite eines Millimeterstrichs auf einem Meßband.

Ein weiteres Beispiel dazu: wenn die Aussage über verschiedene Brechungswinkel wegen unterschiedlicher Geschwindigkeiten stimmen würde, dann müßten sich in einem langen Glasfaserkabel bei jeder Reflexion an der Glaswand die roten und violetten Strahlen voneinander entfernen. Aus einem kompakten Strahl am Anfang des Glaskabels müßte dann am Ende ein breites Regenbogenspektrum werden.
Auf gleicher Ebene befindet sich das Problem der partiellen Reflexion an einer Glasoberfläche. Läßt man 100 Photonen auf eine Glasoberfläche los, dann gehen 96 durch und vier kommen zurück. "Und damit fangen unsere Schwierigkeiten bereits an: Wie ist es überhaupt möglich, daß Licht nur teilweise reflektiert wird? Das eine Photon landet in A, das andere in B - wie 'entscheidet' es sich, wohin es will?" RICHARD FEYNMAN schreibt, daß seine Zuhörer auf diese Bemerkung hin lachten. Er meinte, daß es wie ein Witz klingen mag, aber mit Lachen sei es nicht getan. Hier hat man es mit einem Beispiel zu tun, wo eine gleiche Voraussetzung zu unterschiedliche Resultaten führt. Bei einem einzelnen Photon läßt es sich nicht voraussagen, ob es durch das Glas geht, oder ob es reflektiert wird. Und trotzdem sind am Ende bei hundert Photonen 96 durchgelassen worden und 4 kamen zurück. Die Frage ist nun, woher weiß das fünfzigste Photon, ob es das fünfzigste ist oder das erste oder das hundertste, um entweder durchzugehen oder nicht, damit am Ende die Statistik der Forscher stimmt? Da Photonen ihre eigenen Antiteilchen sind, muß man jede Verbindung die sie herstellen, von beiden Seiten betrachten können. Offensichtlich muß die Frage anders gestellt werden.

Mit der Annahme eines 4-D-Raumes und der zugehörigen Matrixschwingung des uns zugänglichen 3-D in Richtung 4-D, gibt es einen Weg aus dem Problem. Die weitere Voraussetzung ist ein Quantenverhalten des Systems. Ein Stück Masse, in diesem Fall Glas, ist den permanenten 4-D-Matrix-Schwingungen des Raumes ausgesetzt, wobei sich die Atomstruktur diesen Bewegungen anpassen muß. Aufgrund innerer Masseverhältnisse und Quantenverhalten wird bevorzugt ein Zustand eingenommen, bei dem die Materiewellen an der Oberfläche Knoten haben. Dies entspricht einer schwingenden Gitarresaite (Abb. 34a). Kurzzeitig wird allerdings der Energiebetrag zur Aufrechterhaltung dieser Frequenz über- oder unterschritten, und eine neue Quantenschwingung stellt sich ein, deren Länge aber inkompatibel mit der Distanz der Brechungsflächen ist. Dadurch sind keine Knoten an der Oberfläche, sondern Schwingungsbäuche, welche den Durchgang von Photonen verhindern (Abb. 34b), ähnlich wie ein drehender Ventilator Objekte zurückwirft.
Man könnte den Prozeß auch mit einem Klavier vergleichen. Setzt man als Analogie für die Durchgangsbedingungen die Oktaven einer Frequenz, z.B. das 'c', dann wird die Passage gesperrt, wenn bei einer der Oktaven aus dem 'c' ein 'h' oder 'cis' wird. In dieses Modell paßt auch die Erfahrung aus der Optik, daß dünne aufgedampfte Metallschichten den Durchgang einer bestimmten Frequenz ermöglichen, den von anderen jedoch blockieren. Wenn die Schichtdicke der Wellenlänge entspricht, schwingt der Raum an der Stelle mit Knoten an den Endflächen und ermöglicht den Photonen den Durchgang.

Sind die Endflächen zueinander geneigt, wie beim Prisma, dann sind von jedem Eintrittspunkt des Glases aus, den unterschiedlichen Längen der Wellen entsprechend, quantisierte Strecken zum Austritt möglich, die sich fächerförmig aufspalten (Abb 35). Bei einer planparallelen Platte ist dies nicht möglich, da hier die Raummatrix parallel schwingt.
Das Brechungsgesetz muß dann neuformuliert so heißen: Die Raummatrix in festen (flüssigen, gasförmigen ) Objekten schwingt langsamer als im Vakuum. Liegt innerhalb eines Lichtstrahls ein durchsichtiger Körper, so verkürzt dieser durch die von ihm verursachte Raumkrümmung den Abstand zwischen Lichtquelle und Auftreffpunkt. Die Verbindung des Lichtstrahls von der Quelle zum Objekt erfolgt zu Zeitpunkten, an denen die Raummatrix an der Oberfläche des durchsichtigen Körpers Knoten hat. Ist dort ein Schwingungsbauch, wird das auftreffende Photon reflektiert und folgt der Struktur der äußeren Raummatrix. Die Wellenlänge innerhalb des durchsichtigen Körpers hängt vom Material ab. Der Prozentsatz an reflektierten Photonen hängt vom Prozentsatz der Zeit ab, in welcher der Raum an der Grenzfläche Schwingungsbäuche statt Schwingungsknoten hat.
Es besteht eine große Verwirrung in der synonymen Verwendung der Begriffe 'Licht' und 'Photonen'. Ein Photon ist ein einzelnes und quantisiertes Energiepartikel. Seine Energie ist durch einen einzigen Parameter gegeben: die Frequenz. Es ist elektrisch neutral, ohne Masse und hat den Spin 1, d.h. im hier vorgestellten Modell des Torus ist das Verhältnis der Drehungen um beide Torusachsen L und R 1:1.
Von der Regel, daß jedes Teilchen sein separates Antiteilchen hat, macht das Photon eine Ausnahme, denn es ist sein eigenes Antiteilchen. Die daraus folgenden Konsequenzen wurden bisher von wenigen Forschern beachtet. Teilchen und Antiteilchen unterscheiden sich durch die Zeitrichtung. Ein Teilchen wie das Photon, das beide Zeitrichtungen umfaßt, hat logischerweise im 3-D keine Geschwindigkeit: " Zum Beispiel, wir hören manchmal die Aussage, daß ein Lichtsignal von einem Teil der Raumzeit zu einem anderen abgesendet wurde. Die korrekte Ausdrucksweise für diesen Sachverhalt ist zu sagen, daß das Lichtsignal (spannungslos) entlang einer Linie zwischen diesen beiden Teilen der Raumzeit liegt." MICHAEL SHALLIS formuliert es so: “Wenn sich die Zeit in Annäherung an die Lichtgeschwindigkeit verlangsamt, kann man davon ableiten, daß für ein Photon, ein Lichtpartikel, Zeit nicht existiert. Zu diesem Ausmaß kann ein Photon rund um das Universum in Null-Zeit reisen, weil es in seinen Referenzrahmen keine Zeit gibt.”
Photonen sind quantisiert. Der Übertragungsmechanismus dieser Quanten ist aber noch sehr unklar. "Wenn Begriffe nicht anschaulich sind, sind sie noch nicht geklärt. In der Quantenoptik sind sie nicht anschaulich, also sind sie noch nicht geklärt" .
Photonen interagieren nicht miteinander! Ansonsten könnten wir nichts sehen, da sich die Photonen gegenseitig vernichten würden. In einem Raum können sie ungestört jeden Punkt des Raumes mit jedem anderen verbinden. Interaktion, d.h. Interferenz geschieht nicht mit anderen Photonen, sondern mit Masse-besetzten Objekten. Wenn die Zahl der einzelnen Photonen auf einer Brom-Silberschicht energetisch ausreicht das Brom vom Silber zu trennen, wird das Silber frei und wenn man das Brom abwäscht, wird ein schwarzer Silberpunkt sichtbar. Wenn nicht, bleibt die Stelle weiß. Aber untereinander gibt es keine Interferenz.
Der Begriff 'Licht' wird allgemein im Sinn verwendet, daß eine große Zahl von Photonen am Prozeß beteiligt sind, von denen jedes einzelne keine Geschwindigkeit hat und keines mit irgend einem anderen interagiert. "Eine gewöhnliche Glühbirne emittiert in einer milliardstel Sekunde mehr als 100 Milliarden von ihnen." Wenn aber die Geschwindigkeit eines Photons Null ist, dann ist die von einer Billion Photonen ebenfalls Null, denn eine Billion mal Null ist und bleibt Null.
14. 'LICHTGESCHWINDIGKEIT'.
Wie konnte es aber zum Begriff 'Lichtgeschwindigkeit' kommen? Ein Grund ist sicher der, daß die Forscher durch jahrhundertelange Rezeption griechischer Philosophen so hypnotisiert waren, daß sie zwangsläufig ‘Zeit’ und ‘Werden’ mit 'Geschwindigkeit' verbanden. Das krampfhafte Festhalten an der Vorstellung des dreidimensionalen Raumes als Existenzgrundlage tat das übrige dazu. So sahen sie Geschwindigkeiten, wo nur Veränderungen waren und ignorierten geflissentlich Beweise, die auf höherdimensionale Räume hinwiesen. Probleme gab es schon früh, als 1887 ALBERT MICHELSON und EDWARD MORLEY versuchten die 'Lichtgeschwindigkeit' zu messen. Zu ihrer Überraschung waren die 'Geschwindigkeiten' immer gleich, egal in welchem relativen Bewegungszustand man sich zur Lichtquelle befand.
Um das Problem einsichtig zu machen, reduziert man die Dimensionen um eine und betrachtet ein zweidimensionales Geschehen im 2-D. Die Ereignisse im 2-D-Land seien auf einem Film festgehalten, welche einsichtige Wesen im 3-D im Kino anschauen. Der Film im Projektor soll beispielsweise 30 Bilder pro Sekunde vorrücken und die Projektion auf der Leinwand habe 10 Meter Durchmesser. Offensichtlich verändern sich die Dinge im 2-D-Universum und die Wissenschaftler auf der Leinwand bemühen sich nun, die Geschwindigkeit von Lichtstrahlen zwischen zwei Punkten zu messen. Aber egal wie sie messen, die 'Geschwindigkeit' ist immer die Gleiche, sie ist 300 Meter pro Sekunde, egal in welche Richtung sie sich in ihrem 2-D bewegen. Und was sie noch feststellen, diese 300 m/sec sind eine Art 'Grenzgeschwindigkeit', die nicht zu übertreten ist. In ihrem 2-D kann kein Signal von einem Punkt der Leinwand früher zu einem anderen Punkt kommen als nach 1/30 Sekunde (Abbildung 25).
Vom 3-D aus wird der Sachverhalt jedoch klar und ist nicht mehr mysteriös. Wenn eine Person beispielsweise einen Stern erblickt, dann verbindet ein Photon den Stern und das Auge für diesen Augen-Blick. Es gibt keine wirkliche Bewegung der Zeit, in der sich eine Bahn von dem Stern bis zu meinem Auge entwickelt; das ist nur meine Wahrnehmung von meinem Standpunkt aus. Von einem anderen, ebenso gültigen Standpunkt aus ist die Bahn eine ewige Erscheinung, um die herum das Universum sich verändert, und im Laufe dieser Veränderungen im Universum kommt es unter anderem dazu, daß sich mein Auge und der Polarstern zufällig an den entgegengesetzten Enden der Bahn befinden."

Wenn Forscher Ortsveränderungen im Lichtbereich messen, ermitteln sie demnach nicht die 'Lichtgeschwindigkeit' im 3-D, sondern die Geschwindigkeit der Raum-Matrixwellen im 4-D-Raum. Jedes einzelne Photon stellt dabei eine ruhende Verbindungsstrecke im 3-D dar. In diesem Modell besteht somit kein Widerspruch zwischen der Existenz der Photonen außerhalb der Zeit und auf der anderen Seite sichtbaren Veränderungen im 3-D.
Wenn Forscher Ortsveränderungen im Lichtbereich messen, ermitteln sie demnach nicht die 'Lichtgeschwindigkeit' im 3-D, sondern die Geschwindigkeit der Raum-Matrixwellen im 4-D-Raum. Jedes einzelne Photon stellt dabei eine ruhende Verbindungsstrecke im 3-D dar. In diesem Modell besteht somit kein Widerspruch zwischen der Existenz der Photonen außerhalb der Zeit und auf der anderen Seite sichtbaren Veränderungen im 3-D.
Auch für die Komplementäreigenschaften Licht/Welle des Photons ist das 4-D-Modell verwendbar und die Erscheinung eines Photons als Welle oder ein anderes Mal als Teilchen wird unmittelbar einleuchtend.

Die horizontale Ebene in Abb. 26 stellt den um eine Dimension reduzierten 3-D dar. Eine Lichtwelle welche im 4-D die 4-D-Punkte C und D verbindet, schneidet den 3-D in Z und erscheint dann dort als Teilchen. Die gleiche Welle kann aber auch die 4-D-Punkte A und B verbinden, die zudem im Schnitt mit dem 3-D liegen. In diesem Fall wird der Wellencharakter erkennbar. Welcher von den beiden Zuständen sich manifestiert, entscheidet die Vorrichtung. Jedes Photon wird bei der Messung vernichtet. Man kann es also nur einmal messen, entweder als 'Teilchen' oder als 'Welle'.
15. ROTVERSCHIEBUNG.
VESTO M. SLIPHER präsentierte 1914 der Tagung der Astronomischen Gesellschaft die ersten genauen Spektralanalysen von Sternen, wobei sich herausstellte, daß die Linien gegenüber denen im Labor hergestellten, stark verschoben waren. Dies wurde als 'DOPPLEReffekt' interpretiert und EDWIN HUBBLE veröffentlichte zwischen 1925 und 1929 die ersten Arbeiten darüber, wobei als Grundlage die Idee war, dass diese Verschiebung der Spektrallinien zum roten Bereich hin für ein expandierendes Universum sprach. "aber er akzeptierte nie völlig, daß die Rotverschiebung nur von der Radialgeschwindigkeit der Galaxien herrühren sollte."

Wenn man die Konsequenzen der Quantenphysik akzeptiert, stimmt das auch. Das Problem, welches das Wesen der Quantensprünge illustriert, ist der Übergang eines Elektrons von einer Schale der Atomhülle auf eine andere Schale. In Abb. 27a ist ein Übergang eines Elektrons von der K-Schale zur L-Schale skizziert. Dabei gibt es die überflüssige Energie in Form eines Photons ab.
Würden die klassischen Gesetze gelten, dann müßte zwischen dem Aufenthalt in L und der Ankunft in K eine Zeitunterschied zwischen den Zeitpunkten 1 und 2 nachweisbar sein, wie es die untere Kurve in Abb. 67b zeigt. Auf der unteren Achse ist der Abstand zwischen den Elektronenschalen K und L aufgetragen, nach oben die Zeit. Durch die Bewegung würde sich der Energiezustand ändern, der sich durch eine Verbreiterung der Spektrallinie der abgesendeten Photonen zeigen müßte. Dies ist aber nicht der Fall! Also muß der Wechsel der Bahnen in 'Nullzeit' stattfinden, was die obere Linie von Abb. 67b zeigt. "Diese scheinbar einfache Vorstellung bedeutete in Wirklichkeit einen tiefen Bruch mit den klassischen Vorstellungen. Es ist, als würde der Mars aus seiner Bahn verschwinden, unverzüglich in der Bahn der Erde wieder auftauchen und dabei einen Energiestrom ... in den Raum strahlen." Die abgestrahlte Energie ist dabei in feste Größen gepackt und wird sofort, ohne Zeitdifferenz abgegeben! "Man hätte solche Vorstellungen wohl nie ernst genommen, wenn man nicht damit eine ganze Reihe von Experimenten hätte sehr gut und genau erklären können."
Der DOPPLEReffekt
In Abb. 28 ist ein Objekt gegeben, welches sich in einem Medium z.B. Luft bewegt und dabei Schallwellen erzeugt. Wenn das Objekt ruht, breiten sich die Wellen konzentrisch in sphärischer Form aus. Wenn sich das Objekt dabei bewegt, entsteht zwischen der Eigenschwindigkeit des Objektes und der Geschwindigkeit der Schallwellen eine Differenz. Da Schallwellen aber Longitudinalwellen sind, addieren, bzw. subtrahieren sich die Geschwindigkeiten und ein Beobachter von vorne (3) nimmt eine höhere Frequenz war, als sie vom Objekt erzeugt wird. Dahinter (2) erscheint sie tiefer und nur ein seitlicher Beobachter (1) hört die ursprüngliche Frequenz. Ohne das Medium Luft verschwindet der DOPPLEReffekt sofort, da es dann auch keinen Schall mehr gibt. Wichtig ist auch die Schallaussendung in der Zeit und addier- bzw. subtrahierbare Geschwindigkeiten von Objekt und Wellenausbreitung. Beobachter 1 befindet sich rechtwinklig zum Geschehen, weshalb in diesem Zeitpunkt der Dopplereffekt für ihn nicht erfahrbar ist.

Nun wendet man das Ganze auf Licht an. Ende des 19. Jahrhunderts wurde noch über ein Trägermedium für Licht diskutiert, der sogenannte 'Äther', der heute für die Physiker das ist, was der Teufel für den Pfarrer darstellt (wer vom 'Äther' spricht, muß verrückt sein, und diese Besessenheit muß man der Person am besten austreiben). Da es aber nun kein Trägermedium für Licht geben darf, fällt der erste Punkt zur Erzeugung des Dopplereffekts weg.
Wenden wir uns dem nächsten Punkt zu, der Addition und Subtraktion von Geschwindigkeiten. Die Versuche von MICHELSON und MORLEY 1887 zeigten, daß bei einer angenommenen Geschwindigkeit von Licht diese immer gleich ist, egal in welcher relativen Geschwindigkeit man sich dazu bewegt! Anders ausgedrückt, sie ist unabhängig von irgend einem Bewegungszustand im 3-D. Damit ist es aber auch nicht erlaubt, die Geschwindigkeit des lichtaussendenden Objekts von der angeblichen Lichtgeschwindigkeit abzuziehen oder dazuzuzählen. Dies verletzt im Kern die Relativitätstheorie von EINSTEIN. Und wem das noch nicht reicht, der kann noch die Quantenphysik hinzuziehen.

Die Aussendung eines Gammaquants (Photons) erfolgt durch einen Quantensprung eines Elektrons der Atomhülle, in dem das gesamte Photon auf einmal abgeschickt wird (Abb. 29a). Dabei ist aber keine Frequenzänderung möglich, da diese eine Zeitdifferenz erfordert. Geht man aber von einer Verlängerung der Frequenz des Photons aufgrund der Eigengeschwindigkeit v des Objektes aus, so muß die Aussendung des Photons in einer endlichen Zeitdifferenz erfolgen, d.h. die Photonenwelle muß in der Zeit Schwingung für Schwingung das Objekt verlassen (Abb. 29b). Dies verletzt aber die Quantenbedingungen und im Experiment müßte man breite Spektrallinien sehen, was nicht der Fall ist.
Als viertes betrachten wir die Sache auf der mathematisch-physikalischen Ebene. Als Welle ist jedes einzelne Photon unendlich lang ausgedehnt, aber die Geschwindigkeit mit dem Wert 'Unendlich pro Sekunde' gibt es nicht. Das Photon verbindet in Wellenform einfach zwei Punkte im Raum miteinander. Photonen interagieren im freien Raum nie miteinander, sondern nur innerhalb eines Masseobjektes. Als Partikel hat das Photon die Energie im Drehimpuls gespeichert, wobei dieser Impuls genau der Frequenz des Photons proportional ist. Drehimpulse sind aber unabhängig von linearer Geschwindigkeit. Nimmt man in einem Auto einen schwarzen Kreisel mit und markiert den Rand mit einem weißen Strich, so können sowohl die Passagiere wie auch Passanten auf der Straße genau die Anzahl der Drehungen zählen. Die linearen Bewegungen ändern nichts am Drehimpuls des Kreisels.
Fazit: Die 'Theorie' über die Rotverschiebung auf Grund einer angeblichen 'Fluchtgeschwindigkeit' der Sterne ist in allen Aspekten falsch!
Der Astrophysiker JAMES TREFIL schreibt dazu: "Ich erinnerte mich an einen Imbiß in einem angesehenen physikalischen Institut, bei dem ein sehr prominentes Mitglied dieser Fakultät (ich würde es nicht wagen, ihn durch die Erwähnung seines Namens in Verlegenheit zu bringen) sagte, er spiele oft mit dem Gedanken, einen versiegelten Umschlag zu hinterlassen, der fünfzig Jahre nach seinem Tod geöffnet werden solle. Er enthielte seine Vorhersagen über die Ergebnisse bestimmter wissenschaftlicher Kontroversen. An erster Stelle der Liste, fuhr er fort, stünde die Vorhersage, die Interpretation der Rotverschiebung als Beweis für die Ausdehnung des Universums würde sich als falsch erweisen."
Kritik an der Rotverschiebung äußerte 1952 MAX BORN in einem Brief an ALBERT EINSTEIN , als er schrieb: "Es sieht wirklich so aus, als ob Deine Formel nicht ganz stimmt. Bei der Rotverschiebung sieht es noch schlimmer aus; im Inneren der Sonnenscheibe ist sie viel kleiner, am Rand größer als der theoretische Wert" .
Spektralverschiebung als Raumkrümmungseffekt
ERNST MACH erwähnt in einer Bemerkung, daß er bei der Überlegung für eine Erklärung der Linienspektren die Idee hatte, daß nichtsinnliche Dinge nicht notwendigerweise im sinnlich wahrnehmbaren dreidimensionalen Raum vorgestellt werden müssen: "So kam ich auf Analoga des Raumes von verschiedener Dimensionszahl" . Akzeptiert man höherdimensionale Räume als existent, so gibt es eine einfache Erklärung für vorhandene Rotverschiebung von Lichtspektren, die sogar unterschiedliche Verschiebungen bei Doppelsternen mit einschließt. Als Raummodell nehme ich die Konstruktion von Abb. 30 als Basis.
Da vierdimensionale Raumkonstruktionen nicht gerade üblich sind, werde ich zur Eingewöhnung ein Beispiel vorschalten, welches sich im einsehbaren 2-D abspielt.

Der gekrümmt 2-D hat, wie ich schon oben zeigte, die Form eines Torus im 3-D-Einbettungsraum. Projiziert man die Torusoberfläche auf den 2-D wie in Abb. 30a , so erhält man einen Kreis mit Mittelpunkt, wenn man einen Torus mit Lochdurchmesser Null gewählt hat, ansonsten ist es ein Kreisring. Im Querschnitt erzeugte der Torus im 2-D zwei getrennte Kreise. Die Projektion auf die Ebene ist aber doppelt, da die Ebene den Torus in zwei Hälften schneidet (siehe auch Abschnitt über Kodimension). Legt man auf dem Torus in gleichen Abständen Umfänge an, so erscheinen diese an den Rändern und zur Mitte der Kreisprojektion verdichtet (Abb. 30b). Würde man Volumenelemente des Torus auf den Kreis projizieren, hätten diese die umgekehrte Charakteristik, sie wären zur Mitte hin dichter als nach außen.
Bei der Projektion des 4-D-Hypertorus in dem dreidimensionalen Raum geschieht etwas ähnliches. Der Hypertorus erscheint im 3-D als Kugel mit Mittelpunkt wie in Abb. 30a. Eine einzige Ebene der Hypertorus, wie in Abb. 30b, entspricht in der 3-D-Projektion schon einer ganzen Kugel! Eine analoge Erscheinung hätte man im 2-D. Zweidimensionale Wesen würden ein Kugel als 'Hyperkreis' bezeichnen, wobei ein einziger Kugelschnitt schon einen kompletten Kreis ausfüllt, aber damit hätte man die Kugel genausowenig umfassend beschrieben, wie im vierdimensionalen Fall mit der Kugel den Hypertorus. Der senkrechte Schnitt in Abb. 31a ist ebenfalls ein gültiger Teil des Hypertorus. Die Durchdringung mit der horizontalen Projektion ist nur scheinbar, denn in der 4-D-Wirklichkeit sind sie getrennt.

Wenn nun Licht, wie oben gezeigt wurde, eine Erscheinung des 4-D ist, dann ist die Ausbreitung der Photonen nicht an den 3-D gebunden und sie können auch von außen in den von uns sichtbaren Raum eindringen. Dabei müssen sie sich der Raummatrix anpassen und erfahren eine Wellenlängenänderung, die in Abb. 32 skizziert ist.

Auf der linken Seite sollen sich im gekrümmten 3-D an einer weit entfernten Stelle Doppelsterne oder Quasare befinden. Vom lokalen Beobachter aus kann die Entfernung täuschen, da die Lichtquelle im gleichen Raumsektor 'nah' erscheinen mag. Dies kann aber ein Effekt des gekrümmten Raumes sein, so wie in Abb. 31 auf dem Torus weit auseinanderliegende Punkte in der Projektion nahe beieinander zu liegen scheinen. Indem das Licht die 'Abkürzung' durch den 4-D nimmt, hat es einen gewissen Winkel beim Wiedereintritt in den 3-D und muß sich dort der Raumstruktur anpassen. Um sich nicht von der Skizze irreführen zu lassen, muß man sich daran erinnern, daß vom 4-D aus der 3-D komplett offen vor einem liegt. Man kann dann auch z.B. von innen in Objekte einsehen.
In Abb. 32b sieht man, daß die Wellenlänge des Lichts beim durchkreuzen des 3-D eine Verlängerung erfährt, da die ursprüngliche Länge einer Kathede und der Abstand im 3-D der Hypothenuse eines rechtwinkligen Dreiecks entspricht. Bei gleicher Kathede verlängert sich die Hypothenuse mit zunehmendem Einfallswinkel vom 4-D. Je paralleler der Winkel, um so weniger geht die Wellenlängenverschiebung zum roten Bereich. Bei diesem Modell des Universums ist es notwendig, daß Doppelsterne, die im Bezug zu einem bestimmten Beobachter unterschiedliche Winkel aufweisen, unterschiedliche Rotverschiebung haben. Damit könnte man die Daten von verschiedenen Quasaren erklären.
Aber dieser Effekt könnte auch innerhalb des 3-D-Raumes auftreten, wenn nämlich durch große Masseanhäufungen der Raum in sich gekrümmt ist. Zwar ist innerhalb des 3-D diese Krümmung nicht direkt erfahrbar, aber von einem Beobachter außerhalb des 3-D würde dies durch eine Verdichtung der Raummatrix erkennbar sein. Da Photonen aber 4-D-Erscheinungen sind, treffen sie dann vom 4-D aus in einem Winkel zur 3-D-Raummatrix am Beobachtungsort ein und erfahren dort in gleicher Weise wie in Abb. 32 eine Verlängerung der Wellenlänge.
Mit diesem Modell könnte man die Eigenschaften des Quasars 3 C 279 als Zweikomponentensystem erklären, über die P.STUBBS berichtete , dessen beiden Komponenten sich angeblich ‘auseinanderbewegen’. Wenn man die Rotverschiebung als Fluchtgeschwindigkeit interpretiert, kommt man auf das zehnfache der 'Lichtgeschwindigkeit'. Ebenfalls hätte man Erklärungen für die von HALTON ARP gefundenen Galaxienpaare, deren Teile aufgrund der bisher geltenden Theorien unterschiedliche Geschwindigkeiten haben müßten, die sich um das zehnfache unterscheiden. Das ist, als würde man behaupten, bei einem Fahrrad würde das Vorderrad sich mit 10 km/h und das Hinterrad mit 100 km/h bewegen. In 16 Fällen fand ARP bei jüngeren Tochtergalaxien eine höhere Rotverschiebung als bei den älteren Muttergaklaxien. Die erste Reaktion der Astronomen war, daß sie diese Beobachtung als 'optische Täuschung' bezeichneten. "Der Widerstand der Astronomen, ihre Beobachtungszeit auf die Verfolgung der Gedanken Arps zu verwenden, ist vielleicht analog zu der Abneigung zu sehen, die fast alle Wissenschaftler gegen den ‘siebten Sinn', die außersinnliche Wahrnehmung, hegen."
16. LICHTBRECHUNG IN DURCHSICHTIGEN OBJEKTEN
In den Physikbüchern steht, daß in durchsichtigen Körpern die 'Lichtgeschwindigkeit' c eine Funktion der Frequenz sei. Die daraus folgende Abhängigkeit der Brechzahl n eines Körpers von der Frequenz nennt man Dispersion. Die unterschiedlichen 'Geschwindigkeiten' des Lichts im Glas seien angeblich auch für die Brechung (Abb. 33a) verantwortlich. Läßt man einmal den Punkt beiseite, daß die Photonen keine Geschwindigkeit haben, so ergibt sich ein weiterer Widerspruch mit der Erklärung des Verhaltens von Licht an einer planparalleln Platte (Abb. 33b). Hier, so heißt es, werde das Licht nur parallel verschoben, gehe aber ansonsten unverändert durch. Den Widerspruch erkennt man durch zwei aneinandergelegte Prismen (Abb. 33c).
Diese zwei Prismen ergeben eine planparallele Platte, also dürfte sich das Licht nicht aufspalten. Da es aber Prismen sind, müßte die Aufspaltung trotzdem stattfinden. Und, was interessant ist, das Licht müßte am Anfang beim Eintreten schon 'wissen', welchen Winkel die andere Glasseite hat, um sich zu entscheiden ob der Strahl aufgespalten wird oder nicht. Nun könnte man kommen und sagen, die Aufspaltung finde zwar immer statt, aber der Effekt sei so klein, daß man ihn vernachlässigen könne. Das stimmt leider nicht. Bei Flintglas, das einen großen Dispersionsindex hat, müßte man den Effekt bei nur 1 cm dicken Glas schon mit bloßem Auge sehen, denn die Aufspaltung müßte ca 1/10 Millimeter sein (!), etwa in der Größenordnung der Breite eines Millimeterstrichs auf einem Meßband.

Ein weiteres Beispiel dazu: wenn die Aussage über verschiedene Brechungswinkel wegen unterschiedlicher Geschwindigkeiten stimmen würde, dann müßten sich in einem langen Glasfaserkabel bei jeder Reflexion an der Glaswand die roten und violetten Strahlen voneinander entfernen. Aus einem kompakten Strahl am Anfang des Glaskabels müßte dann am Ende ein breites Regenbogenspektrum werden.
Auf gleicher Ebene befindet sich das Problem der partiellen Reflexion an einer Glasoberfläche. Läßt man 100 Photonen auf eine Glasoberfläche los, dann gehen 96 durch und vier kommen zurück. "Und damit fangen unsere Schwierigkeiten bereits an: Wie ist es überhaupt möglich, daß Licht nur teilweise reflektiert wird? Das eine Photon landet in A, das andere in B - wie 'entscheidet' es sich, wohin es will?" RICHARD FEYNMAN schreibt, daß seine Zuhörer auf diese Bemerkung hin lachten. Er meinte, daß es wie ein Witz klingen mag, aber mit Lachen sei es nicht getan. Hier hat man es mit einem Beispiel zu tun, wo eine gleiche Voraussetzung zu unterschiedliche Resultaten führt. Bei einem einzelnen Photon läßt es sich nicht voraussagen, ob es durch das Glas geht, oder ob es reflektiert wird. Und trotzdem sind am Ende bei hundert Photonen 96 durchgelassen worden und 4 kamen zurück. Die Frage ist nun, woher weiß das fünfzigste Photon, ob es das fünfzigste ist oder das erste oder das hundertste, um entweder durchzugehen oder nicht, damit am Ende die Statistik der Forscher stimmt? Da Photonen ihre eigenen Antiteilchen sind, muß man jede Verbindung die sie herstellen, von beiden Seiten betrachten können. Offensichtlich muß die Frage anders gestellt werden.

Mit der Annahme eines 4-D-Raumes und der zugehörigen Matrixschwingung des uns zugänglichen 3-D in Richtung 4-D, gibt es einen Weg aus dem Problem. Die weitere Voraussetzung ist ein Quantenverhalten des Systems. Ein Stück Masse, in diesem Fall Glas, ist den permanenten 4-D-Matrix-Schwingungen des Raumes ausgesetzt, wobei sich die Atomstruktur diesen Bewegungen anpassen muß. Aufgrund innerer Masseverhältnisse und Quantenverhalten wird bevorzugt ein Zustand eingenommen, bei dem die Materiewellen an der Oberfläche Knoten haben. Dies entspricht einer schwingenden Gitarresaite (Abb. 34a). Kurzzeitig wird allerdings der Energiebetrag zur Aufrechterhaltung dieser Frequenz über- oder unterschritten, und eine neue Quantenschwingung stellt sich ein, deren Länge aber inkompatibel mit der Distanz der Brechungsflächen ist. Dadurch sind keine Knoten an der Oberfläche, sondern Schwingungsbäuche, welche den Durchgang von Photonen verhindern (Abb. 34b), ähnlich wie ein drehender Ventilator Objekte zurückwirft.
Man könnte den Prozeß auch mit einem Klavier vergleichen. Setzt man als Analogie für die Durchgangsbedingungen die Oktaven einer Frequenz, z.B. das 'c', dann wird die Passage gesperrt, wenn bei einer der Oktaven aus dem 'c' ein 'h' oder 'cis' wird. In dieses Modell paßt auch die Erfahrung aus der Optik, daß dünne aufgedampfte Metallschichten den Durchgang einer bestimmten Frequenz ermöglichen, den von anderen jedoch blockieren. Wenn die Schichtdicke der Wellenlänge entspricht, schwingt der Raum an der Stelle mit Knoten an den Endflächen und ermöglicht den Photonen den Durchgang.

Sind die Endflächen zueinander geneigt, wie beim Prisma, dann sind von jedem Eintrittspunkt des Glases aus, den unterschiedlichen Längen der Wellen entsprechend, quantisierte Strecken zum Austritt möglich, die sich fächerförmig aufspalten (Abb 35). Bei einer planparallelen Platte ist dies nicht möglich, da hier die Raummatrix parallel schwingt.
Das Brechungsgesetz muß dann neuformuliert so heißen: Die Raummatrix in festen (flüssigen, gasförmigen ) Objekten schwingt langsamer als im Vakuum. Liegt innerhalb eines Lichtstrahls ein durchsichtiger Körper, so verkürzt dieser durch die von ihm verursachte Raumkrümmung den Abstand zwischen Lichtquelle und Auftreffpunkt. Die Verbindung des Lichtstrahls von der Quelle zum Objekt erfolgt zu Zeitpunkten, an denen die Raummatrix an der Oberfläche des durchsichtigen Körpers Knoten hat. Ist dort ein Schwingungsbauch, wird das auftreffende Photon reflektiert und folgt der Struktur der äußeren Raummatrix. Die Wellenlänge innerhalb des durchsichtigen Körpers hängt vom Material ab. Der Prozentsatz an reflektierten Photonen hängt vom Prozentsatz der Zeit ab, in welcher der Raum an der Grenzfläche Schwingungsbäuche statt Schwingungsknoten hat.
-
nicole6

- ModeratorIn

- Beiträge: 2333
- Registriert: 11.09.2009, 13:01
- Wohnort: München
- Ich bin: ehemalige SexarbeiterIn
RE: Diskussionspapier: Modell für Zeit und Raum
17. QUANTENVERHALTEN DURCHSICHTIGER KÖRPER
Im ersten Moment mag es seltsam erscheinen, daß der Durchgang von Licht durch Glas und andere durchsichtige Medien von Quantensprüngen abhängen soll, wenn die Erregung Wellencharakter hat, die, wie man weiß, sinusförmigen Verlauf hat, und stetig dargestellt wird . E. C. ZEEMAN hat 1972 ein Spielzeug erfunden, mit dem man dieses Verhalten real studieren kann . Eine neuere Beschreibung dieser ZEEMAN'schen 'Katastrophenmaschine' findet man im Buch Katastrophentheorie von PETER TIMOTHY SAUNDERS . Die Konstruktion ist in Abb. 36 skizziert.
Man nimmt zwei Gummibänder gleicher Länge welche die Einheit 1 haben soll. Aus einem Karton schneidet man dann einen Kreis dessen Durchmesser ebenfalls die Einheit 1 hat. Mit einem Reißnagel fixiert man nun den Kreismittelpunkt M so auf einen Holzbrettchen oder einem festen Karton, daß sich die Scheibe leicht drehen kann. Im Abstand von 2 Einheiten fixiert man bei F ein Ende eines Gummis und das andere am Rand R des Kreises. Dort wird auch der zweite Gummi mit einem Ende befestigt und das Ende E bleibt frei.
Nun kann man das Ende des freien Gummis in der Gegend herumziehen. Entsprechend der vorherrschenden Spannungen wird sich die Kreisscheibe in einem bestimmten Winkel * einstellen. Den gleichförmigen Bewegungen von E folgt eine gleichförmige Winkeländerung von *. Aber in einem bestimmt Abstand wird man Sprünge feststellen, wo die Scheibe plötzlich in einen neuen Zustand übergeht und auf die andere Seite kippt. Markiert man die Stelle der Quantensprünge, so ergibt sich eine Kurve, die etwa wie der Stern ABCD in Abb. 74 ausschaut. Nimmt man den Randpunkt R als Referenzpunkt und beginnt z.B. die Bewegung des Endpunktes E von CD aus in Richtung AB, so kippt der Punkt R der Scheibe beim Erreichen der Kurvenlinie in einem Sprung nach oben. Bei der Rückwärtsbewegung kippt das System nach den Linien BC und CD wieder in den 'unteren' Zustand. Nur wenn man über B nach links hinausgeht, erfolgen keine Sprünge mehr.
Man sieht aus diesem kleinen Spielzeug, daß auch im Falle eines glatten Potentials diskontinuierliches Verhalten auftreten kann. SAUNDERS weist noch auf ein System von POSTON hin, welches mit Gravitation funktioniert. Man schneidet aus Karton zwei glatte Parabelkurven aus und klebt sie in einem gewissen Abstand durch Holzstückchen oder gefalteter Pappe zusammen. Auf einer Seite der Parabel klebt man ein Metallstück und stellt das Modell dann auch die Kurvenseite. Das Gewicht des Metalls läßt das Parabelmodell auf eine Seite kippen. Bewegt man nun einen Magneten nahe am Metallstück vorbei, so kippt das Modell ab einem gewissen Punkt plötzlich auf die andere Seite.
Hat man nun eine Schwingung, die so gelagert ist, daß sie die gepunktete Kreislinie in Abb. 36 abläuft, so ist das System die meiste Zeit im unteren Zustand und wechselt nur kurzzeitig in den oberen über. Statt einer Kreislinie kann man auch eine lineare Schwingung nehmen, oder eine, deren Kreisbewegung rechtwinklig zur Ebene der Scheibe liegt. Wenn man die Verweilzeit des Systems im oberen Bereich im Verhältnis zur gesamten Schwingungszeit mit 4% ansetzt, hat man ein Modell für die Reflexion von Photonen an durchsichtigen Körpern. Solange das System sich 'unten' befindet, geht das Licht durch, weil an den Grenzflächen Knoten sind; und in 4% der Zeit ist es im 'oberen' Bereich mit Schwingungsbäuchen an den Oberflächen.
18. TOPOLOGIE DES TORUS. FOLGERUNGEN AUS DER DYNAMIK.
Interessant wird es dann, wenn man die schon bekannten Theorien über Wirbelbildung in Torusform auf die postulierten Raumkrümmungseigenschaften anwendet. Die Torusform ist die einzig bekannte Form, in der sich Strömungen von Medium-in-Medium über längere Zeit stabilisieren können. Ein Beispiel dafür sind Rauchringe, Hurrikane, Tornados oder Wasserwirbel (z.B. der Abflußwirbel bei der Badewanne). Die Lebensdauer der zuletzt genannten Erscheinung wurde lange unterschätzt. RUDOLPH H. KÄSE und WALTER ZENK berichten über Meddies (Mediterranean Water Eddies) , die in 1000 Meter Tiefe zwei Jahre lang stabil bleiben und dabei bis zu 1000 Kilometer weit kommen . Auch Torusformen von Luft-in-Luft halten recht lange: "Die mit zyklonalen Wirbeln gekoppelten troposphärischen Kaltlufttropfen sind häufig recht zählebig und lassen sich manchmal durch mehrere Wochen hindurch verfolgen." Wenn sie kleiner sind, halten sie trotzdem bemerkenswert lange, wobei der Meteorologe WARREN FAIDLEY als Zwölfjähriger eine interessante Erfahrung hatte. Mit seinen Freunden wettete er einmal (natürlich ohne Wissen der Eltern), daß er mit seinem Fahrrad in eine Windhose hineinfahren will. Ein Jahr lang machen sie in der Steppe die ihr Haus umgibt, Jagd auf Windhosen, bis er es eines Tages schafft, in ein größeres Exemplar hineinzufahren. Er wird dann zwar durch den Wirbel vom Rad gerissen, kann aber den Wirbel von innen anschauen. Es ist total windstill, schreibt er, kein Stäubchen rührt sich. Umgeben ist er von einem wirbelnden, runden, orangenfarbenen Turm, in den Zeitungspapier, Äste, Blätter und andere Gegenstände eingefügt sind. Schaut er nach oben, sieht er den blauen Himmel durch das Loch am Ende des Schlauches. Seine Freunde auf der Außenseite sind zu Tode erschrocken, sie können ihn nicht mehr sehen und denken, er wurde von der Windhose nach oben gerissen. Für eine Minute kann er mit seinem Fahrrad im 15 Meter dicken Schlauch herumfahren, bis er von einer Wand wieder eingeholt und das zweitemal vom Rad gerissen wird.
Ein sehr starkes Wirbelsystem in Luft ist der Tornado. Topologisch stellt er einen langgestreckten Torus dar. Nach C. A. MARCHAJ ist der Geschwindigkeits- und Druckverlauf innerhalb eines Tornados im Querschnitt wie in Abb. 37.
Wie man in der Skizze sieht, fällt die Geschwindigkeit im Kern rapide auf Null ab. Die gute Sichtbarkeit der Tornados, bei denen die Luft mit Geschwindigkeiten bis zu 140 Meter pro Sekunde rotiert, kommt vom Wasserdampf, welcher sich durch die adiabatische Abkühlung kondensiert. Der große Druckunterschied ist auch für die hohen Schäden der Tornados verantwortlich . po bedeutet in Abb. 37 den Druck in größerer Entfernung des Wirbels.
Nun behaupte ich nicht, daß die folgenden Ausführungen wirklich stimmen, es sind nur Überlegungen, zu welchen Schlußfolgerungen man mit etwas geänderten Voraussetzungen kommt. Nimmt man diesen Druckverlauf des Tornados als Analogie für die Dynamik der Topologie des 4-D-Raumes, so könnte man sich folgenden Vorgang als Prozeß zur Massebildung vorstellen. Bilden sich, aus Gründen die separat zu ermitteln sind, in der Topologie des Raumes Torusformen mit sehr hoher dynamischer Energie, so sinkt der Energielevel im Inneren durch adiabatische Abkühlung so stark ab, daß ein neuer dichterer Phasenzustand entsteht, den wir gewöhnlich als 'Masse' der Atomkernteilchen wie z.B. Protonen und Neutronen kennen .
Aber nicht alle Energie ist im kondensierten Zustand konzentriert. Ein Rest bleibt als 4-D-Toruswirbel erhalten, der den Kern im kondensierten Zustand erhält. Als diskretes Energiesystem formt sich ein fraktaler Torus mit der fraktalen Dimension 1,37. Vom 3-D aus ist der 4-D-Torus nur als 3-D-Sphäre zu erkennen. Allerdings, einmal kondensiert, ist der Kern einigermaßen stabil gegen eine Rückumwandlung. Beim Wasser kennt man einen ähnlichen Effekt. Wenn sich Eis einmal gebildet hat, bleibt es auch ohne Kühlung eine zeitlang im einmal eingenommenen Phasenzustand.
Die Form des Torus zur Massebildung ergibt sich auch aus einer anderen Überlegung. Da Energie quantisiert ist, unterliegt sie bestimmten Regeln der diskreten Chaos-Dynamik. Um stabile Formen einzunehmen, muß ein Attraktor vorgegeben sein, und im 3-D ist die wahrscheinlichste Form ein Torus, wie schon POINCARÉ bemerkte. Damit wird ein Modell für Substrukturen der Elementarteilchen möglich, das einige Probleme löst.
Von Eis weiß man, daß es mit der Zeit seine kondensierte Struktur verändert und unter Druck dichter wird. Falls die hier geäußerte Hypothese stimmt, sollte man einen analogen Effekt auch bei kondensierter Raumenergie feststellen können.
1883 fertigte man aus Platin-Iridium einen Zylinder an, der zum Ur-Kilogramm ernannt wurde. 1889 wurden 42 weitere Muster für verschiedene Länder gemacht. Bei jedem neuen darf die Abweichung nicht mehr als ein fünfzig Millionstel Gramm vom Urstück abweichen. 1988 entdeckte man bei Vergleichswägungen, daß das Urkilogramm angeblich leichter geworden sei. Die anderen 33 Gewichte könnten nicht gleichmäßig schwerer geworden sein.
Aus quanten- und chaostheoretischen Gründen müssen sich zeitstabile Systeme verändern, da statische Zustände hochgradig instabil sind. Damit die kondensierte Kernmasse von Atomen ihren dichten Zustand erhält, muß der Raumenergiezufluß um einen winzigen Betrag größer sein als der Abfluß, sonst würde die kondensierte Raumenergie wieder expandieren. Die Zunahme an Masse-Energie ist am Anfang der Massebildung größer als später. Wenn man Versuche in dieser Richtung machen würde, könnte man sicher auch eine Halbwertszeit der Gewichtszunahme für Massen ermitteln. Mit diesem Wert könnte man dann wiederum das Entstehungsalter der Masse bestimmen
Somit werden auch neu geformte Massen schneller schwerer als ältere. Also ist nicht das alte Urkilogramm leichter, sondern die neu gegossenen Vergleichskilogramme sind schneller schwerer geworden. Die Differenz der Schwerezunahme wurde von den Forschern gemessen.
Torusbildung aus linearer Dynamik.
Noch vor den Gebrüdern WRIGHT hatte F. W. LANCHESTER 1897 ein Patent angemeldet, welches an den Spitzen von Flugzeugflügeln Endscheiben vorsah, um Verwirbelungen und damit Energieverluste zu vermeiden. Die Verwirbelung entsteht deshalb, weil die oberen und unteren Strömungen der Luft hinter dem Flügel in einem gewissen Winkel zueinander liegen. Durch die Zähigkeit der Luft bildet sich die Trennschicht dieser Strömungen hinter dem Flügel aus einer schraubenförmigen Bewegung, die sich zuerst in viele kleine Wirbel aufteilt, um schließlich einen Zopf zu formen, wie es in Abb. 38a skizziert wurde. Die Skizze wurde nach Aufzeichnungen vom LANCHESTER angefertigt . Auch in Wasser bilden sich diese dynamischen Muster, über die L. HELMHOLTZ 1868 eine Studie veröffentlichte . Weitere Forschung folgte von A. OVERBECK (1877), W. BEZOLD (1885), J. J. THOMSON und H. F. NEWALL. (1885) und EMIL HATSCHECK (1918). Eine ausführliche Ausarbeitung und Anwendung auf biologische Topologien wurde dann von D'ARCY THOMPSON vollzogen .
Um diese Kenntnisse als Analogie auf den Raum anwenden zu können, muß man der Raumenergie eine gewisse 'Zähigkeit' zuschreiben. Anders ließe sich auch nicht eine Grenzgeschwindigkeit für Objekte im Raum erklären. Dann kommt dazu, daß die Energie in diskreten Quanten existiert und nach den Regeln der Chaostheorie - selbst bei idealisiertem linearem Fluß - irgendwann eine Abweichung auftreten muß. Das ist dann der Beginn der Verwirbelung (Abb. 38b), die am Schluß in einem Wirbelzopf endet.
LANCHESTER stützte sich bei seinen Veröffentlichungen auf eine Lehrsatz der Theorien von HELMHOLTZ welche besagt, daß ein einmal begonnener Wirbel eines Mediums im Medium nicht frei enden kann, sondern entweder an einer festen Wand anliegen, oder in sich geschlossen sein muß, d.h. einen Toruswirbel bilden. Solche geschlossenen Toruswirbel sind aus der Aerodynamik bekannt: Die Zirkulation am Tragflügel, der Anfahrwirbel und die beiden Randwirbel bilden eine gemeinsame Schraubenlinie. Es ist aus der Abb. 38 ersichtlich, daß der sich formende Torusring kein einschichtiges Produkt ist, sondern in sich viele kleinere Torusformen aufnimmt, welche um die größeren herumkreisen. Um die kleinere Ringe gibt es dann noch kleinere. Damit sind wir wieder beim Modell des fraktalen Torus mit seiner fraktalen Raumdimension 1,37 angelangt, einer Zahl, deren Ziffernfolge der Feinstrukturkonstante * verdächtig ähnlich ist.
Quarks und die Torusform: Leptonen.
Wie weit kommt man wohl mit der Spekulation, daß die Elementarteilchen und ihre Substrukturen, die Quarks, die geometrische Topologie des Torus haben? Das Folgende zeigt die Konsequenzen. In Abb. 39 ist ein Torus skizziert, in dem die Rotationen um die beiden Achsen im Verhältnis 1/2 stehen, d.h. das Objekt muß sich 'zweimal drehen um einmal voll gedreht zu haben'. Im Einklang mit den zuvor ausgeführten Ideen wird ein vierdimensionaler Torus angenommen. Um eine 3-D-Darstellung zu ermöglichen, wurden die x- und y-Achse zu einer zusammengefaßt. Bei einer Drehung der L-Achse um 360* ist die R-Achse um 180* gedreht worden. Es bedarf also einer weiteren 360* Drehung um L, damit alle Punkte des Torus wieder am gleichen Ort angelangt sind.
Nun setzen wir einmal willkürlich die Drehung um die L-Achse beim Spin 1/2 mit dem Begriff 'Ladung' gleich, die wir mit Q abkürzen und betrachten den Durchfluß des Torus durch eine Kontrollfläche, wie die bei der VI. Phase in Abb. 39. Der Torus in Abb. 39 hat zum einfacheren Verständnis ein Mittelloch. Hier nehmen wir aber einen ohne Mittelloch. Bei einer Drehung durchläuft die Mittellinie des Torus demnach die Strecke 2r*, was der Ladung Q entsprechen soll: Q = 2r*. Bei einem Torus ohne Mittelloch ist aber die Oberfläche des Torus ebenfalls 2r* und die gesamte Oberfläche, die sich bei einer Drehung durch die Kontrollfläche bewegt ist damit 4*2r2 = Q².
In den obigen Ausführungen habe ich gezeigt, daß die Schwingungsfrequenz der 3-D-Raummatrix dem Wert der sogenannten 'Lichtgeschwindigkeit' entspricht, also 'c'. Ist der zeitliche Drehtakt des Torus damit synchron, muß man ihn durch c dividieren und wir sind bei Q²/c angelangt. Da wir aber auch noch eine quantisiertes Objekt vor uns haben, dividieren wir noch durch die HEISENBERG-Konstante h/2* und erhalten insgesamt 2*Q²/ch. Dies ist zur Überraschung die gleiche Formel, welche von den Physikern für die Feinstrukturkonstante Alpha angegeben wird, wenn man für Q die Elektronenladung nimmt!
Zwei-Quark-Teilchen: Mesonen.
Die Ein-Quark-Teilchen werden in der Gruppe der 'Leptonen' zusammengefaßt. Teilchen mit 2 Quarks heißen allgemein 'Mesonen'. Der Schnitt von zwei Torusformen ineinander ist in Abb. 40 wiedergegeben. Jeder Teil-Torus kann unterschiedliche Bewegungszustände einnehmen, die sich dann jeweils überlagern. Die Kombinationen aus den Drehungen um die L- und R-Achsen werden von den Forschern mit 'Farbe' benannt. 'Antifarbe' entspricht dann der entgegengesetzten Drehung.
In Abb. 40 hat der äußere Torus des **-Mesons den Spin -1/2, der innere +1/2. Der Spin ist dann von außen gesehen bei allen Mesonen Null, da sich die entgegengesetzten Drehungen um die R-Achse insgesamt aufheben. Da wir die Rotation um die Zentralachse mit 'Ladung' gleichgesetzt haben, muß die Gesamtladung im dargestellten Fall Null sein. Wenn sich allerdings beide Schichten um die L-Achse gleichsinnig drehen, dann wird die Ladung Eins oder minus Eins.
Nun entsteht die Frage, was an der Grenzschicht der beiden gegenläufigen Torusschläuchen geschieht. Aus Studien an turbulenten Strömungen weiß man, daß sich hier fraktale Formen bilden, in diesem Fall sind es kleinere Torusformen, welche sich im Zwischenbereich den beiden größeren befinden. Sie fungieren wie die Kugeln in einem Kugellager. In Flüssen kann man an gegenläufigen Strömungen den gleichen Effekt beobachten. Bei atomaren Teilchen werden sie 'Isospin' genannt. In Abb. 41 ist ein Viertelschnitt durch ein Meson wiedergegeben.
Jetzt ist klar, daß einfache Teilchen wie die Leptonen keinen Isospin haben können, der kann erst bei mindestens zwei Unterteilungen auftauchen. Möglich ist auch, daß sich zwischen den Torusformen des Isospins noch feinere Strukturen befinden, die insgesamt eine fraktale Dimension von 1.37 bilden. Wenn beide Torusschläuche sich nicht bewegen, wie im Fall des *º, ist die Lebensdauer um das millionenfache kürzer, wie man aus der Tabelle entnehmen kann. Bei L=0 und R gegenläufig (keine Ladung, kein Spin) ergibt sich ein Isospin 1. Relativ gesehen lang ist die Dauer, wenn L für den inneren und äußeren Torus gleichsinnig und R gegensinnig dreht wie beim *+- oder *--Teilchen.
Mit den drei Größen Ladung (Drehung um die L-Achse), Spin (Drehung um die R-Achse) und Isospin (Drehung der Zwischenschicht) ist ein Dreibein gegeben, das man ausrichten kann und den Wert der Parität zuordnen, wie es in obigen Beispielen schon mehrmals geschah. Offensichtlich war dies bei den Leptonen nicht möglich, da diese nur 2 Größen hatten, die L- und R-Achse.
Drei-Quark-Teilchen: Baryonen.
Hier findet man die bekanntesten Atombausteine, die Protonen und Neutronen. Bei drei Zwischenschichten sind natürlich noch mehr Kombinationen möglich als in den vorigen Fällen. In Abb. 42 ist das Beispiel eines Protons gegeben. Die Inneren Schichten bewegen sich gegenläufig. Die Spinwerte sind auf der linken Seite des Aufschnittes gegeben; die Richtungen der u- und d-Quarks auf der rechten. Eine Ladungseinheit mit einer Umdrehung vom 360grad entspricht dem Wert 2pi, die 120grad-Drehung des d-Quarks demnach 2/3pi und 240pi des u-Quarks 4/3pi.
Zählt man die Spins zusammen, kommt man auf +½ -½ +½ = ½. Bei den Ladungsteilen ist der Wert +4/3pi -2/3pi +4/3pi = 2pi, d.h. eine volle Umdrehung mit der Ladungseinheit +1.
Der Isospin hat zwei Komponenten. Eine entsteht zwischen dem äußeren u- und d, das zweite zwischen dem inneren u- und dem mittleren d-Quark. Die Drehachsen sind parallel, aber gegenläufig, wodurch sich der Wert des Isospins für eine Schicht halbiert, da sich d zu u wie 1/2 verhält. Insgesamt summieren sich die Werte wieder zu ¼+¼=½ auf.
An dieser Stelle muß ich nochmals darauf hinweisen, daß der Aufschnitt von Abb. 42 nur einen Teilaspekt des gesamten 4-D-Torus darstellt! Aus Abb. 42 wird ersichtlich, daß der obige Torus im Verhältnis zum 4-D-Modell wie der Querschnitt einer Kreisscheibe zum 3-D-Torus steht.
Sind bei einem Teilchen alle drei Spins gleichgerichtet, so addieren sie sich zu 3/2 und da es dann auch keine Rotation der Zwischenschichten gibt, wird der Isospin Null, wie man beim Omega¯-Teilchen sieht.
Lagert man an einem Proton zusätzlich ein Elektron an, verschwindet nach außen hin die Ladung, weil sich die überlagernden Effekte der entgegengesetzten Drehungen +L(p) und -L(e) aufheben . Die Spins sind parallel laufend und entgegensetzt gerichtet. Die Kopplungsschicht dazwischen hat demnach keine Drehung um die L-Achse und ist elektrisch neutral.
Es ist das Antiteilchen des Neutrinos, welches vom Elektron abgeleitet ist. Nach außen erscheint nun diese Teilchenkombination elektrisch neutral und wurde dementsprechend 'Neutron' genannt . Schaut man in die Mesonen-Tabelle, so sieht man, daß die geladenen Teilchen etwas schwerer sind, als die ungeladenen, weil sie zusätzlich noch die Ladungsenergie tragen. Das Neutron macht da keine Ausnahme, es trägt sogar zwei Ladungsteile, den positiven des Protons und den negativen des Elektrons. Aber da diese Ladungen sich innerlich aufheben, erscheint das Teilchen nach außen ungeladen. Erst beim Zerfall in die drei ursprünglichen Partikel wird der Ladungsanteil an der Energie deutlich.
Ein grundlegender Unterschied besteht jedoch zwischen dem Proton und dem Elektron. Während das letztere einen reinen Raumenergiewirbel darstellt, hat das Proton wahrscheinlich einen kondensierten Energiekern der Art, wie er oben im Abschnitt über Massebildung beschrieben wurde. Die Gesamtenergie des Protons ist dann die Summe aus der Energie des Kerns aus verdichteter Energie und der Energie in Torusform, welche eine Hülle um diesen Kern bildet.
Die Frage ist, warum Protonen eine so lange Lebenszeit haben. Schaut man sich die Quarkschichtung an, welche aus Energieschwingungen bestehen, so stehen diese Frequenzen mit dem Spin im Verhältnis von 3 zu 2. Dieses Verhältnis findet man auch bei Gravitationsresonanzen im Asteroidengürtel. Normalerweise ordnen sich entsprechend der Verteilung der wechselnden Kräfte Massebruchstücke an gewissen Orten an, wo wenig Wechsel stattfinden und meiden solche mit vielen Wechseln. Diese Lücken findet man in der Astronomie vorwiegend bei Resonanzverhältnissen der Werte 2:1, 3:1, 4:1, 5:2 und 7:2. Eine Ausnahme bildet 3:2, wo man im Asteroidengürtel die 'Hilda-Gruppe' vorfindet, was zeigt, daß die 3:2 Resonanz etwas besonderes an sich haben muß.
Um das Spezielle der 3:2 Resonanz herauszufinden, bauten STEWARD, APPLEGATE, DOUGLAS, GÜRSEL und SUSSMAN einen speziellen Computer (Digital Orrery), der das Sonnensystem von 100 Millionen Jahren aus der Vergangenheit bis in 110 Millionen Jahren in die Zukunft berechnete. Das Ergebnis: die 3:2 Resonanz ist stabil und nicht chaotisch! "Mathematisch gesehen, ist jede Resonanz ein spezielles Biest mit seinen eigenen Eigenschaften. Es gibt keinen Grund, warum die 3:2 Resonanz sich wie die 3:1 oder 2:1 verhalten soll, wie auch die Zahl 3/2 ungleich 3 und 2 ist. Offensichtlich ist die effektive Abwesenheit von Chaos eine der auffälligen Aspekte der 3:2 Resonanz."
Wahrscheinlich ist es gerade die 3:2 Resonanz der Torushülle, welche dem Proton die lange Lebensdauer gibt. Das Neutron hat schon 2 Schichten mehr (das Antineutrino und das Elektron) weshalb die Lebensdauer kürzer ist und ca 15 Minuten beträgt.
Zusammengehalten werden die Masseteilchen in einem Atom mit einiger Wahrscheinlichkeit durch den doppelten Trichter der Mitte des Toruswirbels, der auch die Reichweite dieser 'Starken Kernkraft' bestimmt. Als Analogie kann man sich verschiedene Trichter vorstellen, die ineinandergesteckt werden. 'Automatisch' werden die Spitzen der Trichter auf einer Linie zu liegen bekommen, egal wie weit man sie von der Mitte weg eingeführt hat, mit der Bedingung, daß sich die Spitze zumindest irgendwo innerhalb des Randes bewegt. Auch die Trennung ist dann schwieriger, da zuerst der Anstieg des Trichterrandes überwunden werden muß.
Im ersten Moment mag es seltsam erscheinen, daß der Durchgang von Licht durch Glas und andere durchsichtige Medien von Quantensprüngen abhängen soll, wenn die Erregung Wellencharakter hat, die, wie man weiß, sinusförmigen Verlauf hat, und stetig dargestellt wird . E. C. ZEEMAN hat 1972 ein Spielzeug erfunden, mit dem man dieses Verhalten real studieren kann . Eine neuere Beschreibung dieser ZEEMAN'schen 'Katastrophenmaschine' findet man im Buch Katastrophentheorie von PETER TIMOTHY SAUNDERS . Die Konstruktion ist in Abb. 36 skizziert.
Man nimmt zwei Gummibänder gleicher Länge welche die Einheit 1 haben soll. Aus einem Karton schneidet man dann einen Kreis dessen Durchmesser ebenfalls die Einheit 1 hat. Mit einem Reißnagel fixiert man nun den Kreismittelpunkt M so auf einen Holzbrettchen oder einem festen Karton, daß sich die Scheibe leicht drehen kann. Im Abstand von 2 Einheiten fixiert man bei F ein Ende eines Gummis und das andere am Rand R des Kreises. Dort wird auch der zweite Gummi mit einem Ende befestigt und das Ende E bleibt frei.

Nun kann man das Ende des freien Gummis in der Gegend herumziehen. Entsprechend der vorherrschenden Spannungen wird sich die Kreisscheibe in einem bestimmten Winkel * einstellen. Den gleichförmigen Bewegungen von E folgt eine gleichförmige Winkeländerung von *. Aber in einem bestimmt Abstand wird man Sprünge feststellen, wo die Scheibe plötzlich in einen neuen Zustand übergeht und auf die andere Seite kippt. Markiert man die Stelle der Quantensprünge, so ergibt sich eine Kurve, die etwa wie der Stern ABCD in Abb. 74 ausschaut. Nimmt man den Randpunkt R als Referenzpunkt und beginnt z.B. die Bewegung des Endpunktes E von CD aus in Richtung AB, so kippt der Punkt R der Scheibe beim Erreichen der Kurvenlinie in einem Sprung nach oben. Bei der Rückwärtsbewegung kippt das System nach den Linien BC und CD wieder in den 'unteren' Zustand. Nur wenn man über B nach links hinausgeht, erfolgen keine Sprünge mehr.
Man sieht aus diesem kleinen Spielzeug, daß auch im Falle eines glatten Potentials diskontinuierliches Verhalten auftreten kann. SAUNDERS weist noch auf ein System von POSTON hin, welches mit Gravitation funktioniert. Man schneidet aus Karton zwei glatte Parabelkurven aus und klebt sie in einem gewissen Abstand durch Holzstückchen oder gefalteter Pappe zusammen. Auf einer Seite der Parabel klebt man ein Metallstück und stellt das Modell dann auch die Kurvenseite. Das Gewicht des Metalls läßt das Parabelmodell auf eine Seite kippen. Bewegt man nun einen Magneten nahe am Metallstück vorbei, so kippt das Modell ab einem gewissen Punkt plötzlich auf die andere Seite.
Hat man nun eine Schwingung, die so gelagert ist, daß sie die gepunktete Kreislinie in Abb. 36 abläuft, so ist das System die meiste Zeit im unteren Zustand und wechselt nur kurzzeitig in den oberen über. Statt einer Kreislinie kann man auch eine lineare Schwingung nehmen, oder eine, deren Kreisbewegung rechtwinklig zur Ebene der Scheibe liegt. Wenn man die Verweilzeit des Systems im oberen Bereich im Verhältnis zur gesamten Schwingungszeit mit 4% ansetzt, hat man ein Modell für die Reflexion von Photonen an durchsichtigen Körpern. Solange das System sich 'unten' befindet, geht das Licht durch, weil an den Grenzflächen Knoten sind; und in 4% der Zeit ist es im 'oberen' Bereich mit Schwingungsbäuchen an den Oberflächen.
18. TOPOLOGIE DES TORUS. FOLGERUNGEN AUS DER DYNAMIK.
Interessant wird es dann, wenn man die schon bekannten Theorien über Wirbelbildung in Torusform auf die postulierten Raumkrümmungseigenschaften anwendet. Die Torusform ist die einzig bekannte Form, in der sich Strömungen von Medium-in-Medium über längere Zeit stabilisieren können. Ein Beispiel dafür sind Rauchringe, Hurrikane, Tornados oder Wasserwirbel (z.B. der Abflußwirbel bei der Badewanne). Die Lebensdauer der zuletzt genannten Erscheinung wurde lange unterschätzt. RUDOLPH H. KÄSE und WALTER ZENK berichten über Meddies (Mediterranean Water Eddies) , die in 1000 Meter Tiefe zwei Jahre lang stabil bleiben und dabei bis zu 1000 Kilometer weit kommen . Auch Torusformen von Luft-in-Luft halten recht lange: "Die mit zyklonalen Wirbeln gekoppelten troposphärischen Kaltlufttropfen sind häufig recht zählebig und lassen sich manchmal durch mehrere Wochen hindurch verfolgen." Wenn sie kleiner sind, halten sie trotzdem bemerkenswert lange, wobei der Meteorologe WARREN FAIDLEY als Zwölfjähriger eine interessante Erfahrung hatte. Mit seinen Freunden wettete er einmal (natürlich ohne Wissen der Eltern), daß er mit seinem Fahrrad in eine Windhose hineinfahren will. Ein Jahr lang machen sie in der Steppe die ihr Haus umgibt, Jagd auf Windhosen, bis er es eines Tages schafft, in ein größeres Exemplar hineinzufahren. Er wird dann zwar durch den Wirbel vom Rad gerissen, kann aber den Wirbel von innen anschauen. Es ist total windstill, schreibt er, kein Stäubchen rührt sich. Umgeben ist er von einem wirbelnden, runden, orangenfarbenen Turm, in den Zeitungspapier, Äste, Blätter und andere Gegenstände eingefügt sind. Schaut er nach oben, sieht er den blauen Himmel durch das Loch am Ende des Schlauches. Seine Freunde auf der Außenseite sind zu Tode erschrocken, sie können ihn nicht mehr sehen und denken, er wurde von der Windhose nach oben gerissen. Für eine Minute kann er mit seinem Fahrrad im 15 Meter dicken Schlauch herumfahren, bis er von einer Wand wieder eingeholt und das zweitemal vom Rad gerissen wird.
Ein sehr starkes Wirbelsystem in Luft ist der Tornado. Topologisch stellt er einen langgestreckten Torus dar. Nach C. A. MARCHAJ ist der Geschwindigkeits- und Druckverlauf innerhalb eines Tornados im Querschnitt wie in Abb. 37.

Wie man in der Skizze sieht, fällt die Geschwindigkeit im Kern rapide auf Null ab. Die gute Sichtbarkeit der Tornados, bei denen die Luft mit Geschwindigkeiten bis zu 140 Meter pro Sekunde rotiert, kommt vom Wasserdampf, welcher sich durch die adiabatische Abkühlung kondensiert. Der große Druckunterschied ist auch für die hohen Schäden der Tornados verantwortlich . po bedeutet in Abb. 37 den Druck in größerer Entfernung des Wirbels.
Nun behaupte ich nicht, daß die folgenden Ausführungen wirklich stimmen, es sind nur Überlegungen, zu welchen Schlußfolgerungen man mit etwas geänderten Voraussetzungen kommt. Nimmt man diesen Druckverlauf des Tornados als Analogie für die Dynamik der Topologie des 4-D-Raumes, so könnte man sich folgenden Vorgang als Prozeß zur Massebildung vorstellen. Bilden sich, aus Gründen die separat zu ermitteln sind, in der Topologie des Raumes Torusformen mit sehr hoher dynamischer Energie, so sinkt der Energielevel im Inneren durch adiabatische Abkühlung so stark ab, daß ein neuer dichterer Phasenzustand entsteht, den wir gewöhnlich als 'Masse' der Atomkernteilchen wie z.B. Protonen und Neutronen kennen .
Aber nicht alle Energie ist im kondensierten Zustand konzentriert. Ein Rest bleibt als 4-D-Toruswirbel erhalten, der den Kern im kondensierten Zustand erhält. Als diskretes Energiesystem formt sich ein fraktaler Torus mit der fraktalen Dimension 1,37. Vom 3-D aus ist der 4-D-Torus nur als 3-D-Sphäre zu erkennen. Allerdings, einmal kondensiert, ist der Kern einigermaßen stabil gegen eine Rückumwandlung. Beim Wasser kennt man einen ähnlichen Effekt. Wenn sich Eis einmal gebildet hat, bleibt es auch ohne Kühlung eine zeitlang im einmal eingenommenen Phasenzustand.
Die Form des Torus zur Massebildung ergibt sich auch aus einer anderen Überlegung. Da Energie quantisiert ist, unterliegt sie bestimmten Regeln der diskreten Chaos-Dynamik. Um stabile Formen einzunehmen, muß ein Attraktor vorgegeben sein, und im 3-D ist die wahrscheinlichste Form ein Torus, wie schon POINCARÉ bemerkte. Damit wird ein Modell für Substrukturen der Elementarteilchen möglich, das einige Probleme löst.
Von Eis weiß man, daß es mit der Zeit seine kondensierte Struktur verändert und unter Druck dichter wird. Falls die hier geäußerte Hypothese stimmt, sollte man einen analogen Effekt auch bei kondensierter Raumenergie feststellen können.
1883 fertigte man aus Platin-Iridium einen Zylinder an, der zum Ur-Kilogramm ernannt wurde. 1889 wurden 42 weitere Muster für verschiedene Länder gemacht. Bei jedem neuen darf die Abweichung nicht mehr als ein fünfzig Millionstel Gramm vom Urstück abweichen. 1988 entdeckte man bei Vergleichswägungen, daß das Urkilogramm angeblich leichter geworden sei. Die anderen 33 Gewichte könnten nicht gleichmäßig schwerer geworden sein.
Aus quanten- und chaostheoretischen Gründen müssen sich zeitstabile Systeme verändern, da statische Zustände hochgradig instabil sind. Damit die kondensierte Kernmasse von Atomen ihren dichten Zustand erhält, muß der Raumenergiezufluß um einen winzigen Betrag größer sein als der Abfluß, sonst würde die kondensierte Raumenergie wieder expandieren. Die Zunahme an Masse-Energie ist am Anfang der Massebildung größer als später. Wenn man Versuche in dieser Richtung machen würde, könnte man sicher auch eine Halbwertszeit der Gewichtszunahme für Massen ermitteln. Mit diesem Wert könnte man dann wiederum das Entstehungsalter der Masse bestimmen
Somit werden auch neu geformte Massen schneller schwerer als ältere. Also ist nicht das alte Urkilogramm leichter, sondern die neu gegossenen Vergleichskilogramme sind schneller schwerer geworden. Die Differenz der Schwerezunahme wurde von den Forschern gemessen.
Torusbildung aus linearer Dynamik.
Noch vor den Gebrüdern WRIGHT hatte F. W. LANCHESTER 1897 ein Patent angemeldet, welches an den Spitzen von Flugzeugflügeln Endscheiben vorsah, um Verwirbelungen und damit Energieverluste zu vermeiden. Die Verwirbelung entsteht deshalb, weil die oberen und unteren Strömungen der Luft hinter dem Flügel in einem gewissen Winkel zueinander liegen. Durch die Zähigkeit der Luft bildet sich die Trennschicht dieser Strömungen hinter dem Flügel aus einer schraubenförmigen Bewegung, die sich zuerst in viele kleine Wirbel aufteilt, um schließlich einen Zopf zu formen, wie es in Abb. 38a skizziert wurde. Die Skizze wurde nach Aufzeichnungen vom LANCHESTER angefertigt . Auch in Wasser bilden sich diese dynamischen Muster, über die L. HELMHOLTZ 1868 eine Studie veröffentlichte . Weitere Forschung folgte von A. OVERBECK (1877), W. BEZOLD (1885), J. J. THOMSON und H. F. NEWALL. (1885) und EMIL HATSCHECK (1918). Eine ausführliche Ausarbeitung und Anwendung auf biologische Topologien wurde dann von D'ARCY THOMPSON vollzogen .
Um diese Kenntnisse als Analogie auf den Raum anwenden zu können, muß man der Raumenergie eine gewisse 'Zähigkeit' zuschreiben. Anders ließe sich auch nicht eine Grenzgeschwindigkeit für Objekte im Raum erklären. Dann kommt dazu, daß die Energie in diskreten Quanten existiert und nach den Regeln der Chaostheorie - selbst bei idealisiertem linearem Fluß - irgendwann eine Abweichung auftreten muß. Das ist dann der Beginn der Verwirbelung (Abb. 38b), die am Schluß in einem Wirbelzopf endet.

LANCHESTER stützte sich bei seinen Veröffentlichungen auf eine Lehrsatz der Theorien von HELMHOLTZ welche besagt, daß ein einmal begonnener Wirbel eines Mediums im Medium nicht frei enden kann, sondern entweder an einer festen Wand anliegen, oder in sich geschlossen sein muß, d.h. einen Toruswirbel bilden. Solche geschlossenen Toruswirbel sind aus der Aerodynamik bekannt: Die Zirkulation am Tragflügel, der Anfahrwirbel und die beiden Randwirbel bilden eine gemeinsame Schraubenlinie. Es ist aus der Abb. 38 ersichtlich, daß der sich formende Torusring kein einschichtiges Produkt ist, sondern in sich viele kleinere Torusformen aufnimmt, welche um die größeren herumkreisen. Um die kleinere Ringe gibt es dann noch kleinere. Damit sind wir wieder beim Modell des fraktalen Torus mit seiner fraktalen Raumdimension 1,37 angelangt, einer Zahl, deren Ziffernfolge der Feinstrukturkonstante * verdächtig ähnlich ist.
Quarks und die Torusform: Leptonen.
Wie weit kommt man wohl mit der Spekulation, daß die Elementarteilchen und ihre Substrukturen, die Quarks, die geometrische Topologie des Torus haben? Das Folgende zeigt die Konsequenzen. In Abb. 39 ist ein Torus skizziert, in dem die Rotationen um die beiden Achsen im Verhältnis 1/2 stehen, d.h. das Objekt muß sich 'zweimal drehen um einmal voll gedreht zu haben'. Im Einklang mit den zuvor ausgeführten Ideen wird ein vierdimensionaler Torus angenommen. Um eine 3-D-Darstellung zu ermöglichen, wurden die x- und y-Achse zu einer zusammengefaßt. Bei einer Drehung der L-Achse um 360* ist die R-Achse um 180* gedreht worden. Es bedarf also einer weiteren 360* Drehung um L, damit alle Punkte des Torus wieder am gleichen Ort angelangt sind.
Nun setzen wir einmal willkürlich die Drehung um die L-Achse beim Spin 1/2 mit dem Begriff 'Ladung' gleich, die wir mit Q abkürzen und betrachten den Durchfluß des Torus durch eine Kontrollfläche, wie die bei der VI. Phase in Abb. 39. Der Torus in Abb. 39 hat zum einfacheren Verständnis ein Mittelloch. Hier nehmen wir aber einen ohne Mittelloch. Bei einer Drehung durchläuft die Mittellinie des Torus demnach die Strecke 2r*, was der Ladung Q entsprechen soll: Q = 2r*. Bei einem Torus ohne Mittelloch ist aber die Oberfläche des Torus ebenfalls 2r* und die gesamte Oberfläche, die sich bei einer Drehung durch die Kontrollfläche bewegt ist damit 4*2r2 = Q².

In den obigen Ausführungen habe ich gezeigt, daß die Schwingungsfrequenz der 3-D-Raummatrix dem Wert der sogenannten 'Lichtgeschwindigkeit' entspricht, also 'c'. Ist der zeitliche Drehtakt des Torus damit synchron, muß man ihn durch c dividieren und wir sind bei Q²/c angelangt. Da wir aber auch noch eine quantisiertes Objekt vor uns haben, dividieren wir noch durch die HEISENBERG-Konstante h/2* und erhalten insgesamt 2*Q²/ch. Dies ist zur Überraschung die gleiche Formel, welche von den Physikern für die Feinstrukturkonstante Alpha angegeben wird, wenn man für Q die Elektronenladung nimmt!
Zwei-Quark-Teilchen: Mesonen.
Die Ein-Quark-Teilchen werden in der Gruppe der 'Leptonen' zusammengefaßt. Teilchen mit 2 Quarks heißen allgemein 'Mesonen'. Der Schnitt von zwei Torusformen ineinander ist in Abb. 40 wiedergegeben. Jeder Teil-Torus kann unterschiedliche Bewegungszustände einnehmen, die sich dann jeweils überlagern. Die Kombinationen aus den Drehungen um die L- und R-Achsen werden von den Forschern mit 'Farbe' benannt. 'Antifarbe' entspricht dann der entgegengesetzten Drehung.

In Abb. 40 hat der äußere Torus des **-Mesons den Spin -1/2, der innere +1/2. Der Spin ist dann von außen gesehen bei allen Mesonen Null, da sich die entgegengesetzten Drehungen um die R-Achse insgesamt aufheben. Da wir die Rotation um die Zentralachse mit 'Ladung' gleichgesetzt haben, muß die Gesamtladung im dargestellten Fall Null sein. Wenn sich allerdings beide Schichten um die L-Achse gleichsinnig drehen, dann wird die Ladung Eins oder minus Eins.
Nun entsteht die Frage, was an der Grenzschicht der beiden gegenläufigen Torusschläuchen geschieht. Aus Studien an turbulenten Strömungen weiß man, daß sich hier fraktale Formen bilden, in diesem Fall sind es kleinere Torusformen, welche sich im Zwischenbereich den beiden größeren befinden. Sie fungieren wie die Kugeln in einem Kugellager. In Flüssen kann man an gegenläufigen Strömungen den gleichen Effekt beobachten. Bei atomaren Teilchen werden sie 'Isospin' genannt. In Abb. 41 ist ein Viertelschnitt durch ein Meson wiedergegeben.

Jetzt ist klar, daß einfache Teilchen wie die Leptonen keinen Isospin haben können, der kann erst bei mindestens zwei Unterteilungen auftauchen. Möglich ist auch, daß sich zwischen den Torusformen des Isospins noch feinere Strukturen befinden, die insgesamt eine fraktale Dimension von 1.37 bilden. Wenn beide Torusschläuche sich nicht bewegen, wie im Fall des *º, ist die Lebensdauer um das millionenfache kürzer, wie man aus der Tabelle entnehmen kann. Bei L=0 und R gegenläufig (keine Ladung, kein Spin) ergibt sich ein Isospin 1. Relativ gesehen lang ist die Dauer, wenn L für den inneren und äußeren Torus gleichsinnig und R gegensinnig dreht wie beim *+- oder *--Teilchen.
Mit den drei Größen Ladung (Drehung um die L-Achse), Spin (Drehung um die R-Achse) und Isospin (Drehung der Zwischenschicht) ist ein Dreibein gegeben, das man ausrichten kann und den Wert der Parität zuordnen, wie es in obigen Beispielen schon mehrmals geschah. Offensichtlich war dies bei den Leptonen nicht möglich, da diese nur 2 Größen hatten, die L- und R-Achse.
Drei-Quark-Teilchen: Baryonen.
Hier findet man die bekanntesten Atombausteine, die Protonen und Neutronen. Bei drei Zwischenschichten sind natürlich noch mehr Kombinationen möglich als in den vorigen Fällen. In Abb. 42 ist das Beispiel eines Protons gegeben. Die Inneren Schichten bewegen sich gegenläufig. Die Spinwerte sind auf der linken Seite des Aufschnittes gegeben; die Richtungen der u- und d-Quarks auf der rechten. Eine Ladungseinheit mit einer Umdrehung vom 360grad entspricht dem Wert 2pi, die 120grad-Drehung des d-Quarks demnach 2/3pi und 240pi des u-Quarks 4/3pi.
Zählt man die Spins zusammen, kommt man auf +½ -½ +½ = ½. Bei den Ladungsteilen ist der Wert +4/3pi -2/3pi +4/3pi = 2pi, d.h. eine volle Umdrehung mit der Ladungseinheit +1.
Der Isospin hat zwei Komponenten. Eine entsteht zwischen dem äußeren u- und d, das zweite zwischen dem inneren u- und dem mittleren d-Quark. Die Drehachsen sind parallel, aber gegenläufig, wodurch sich der Wert des Isospins für eine Schicht halbiert, da sich d zu u wie 1/2 verhält. Insgesamt summieren sich die Werte wieder zu ¼+¼=½ auf.
An dieser Stelle muß ich nochmals darauf hinweisen, daß der Aufschnitt von Abb. 42 nur einen Teilaspekt des gesamten 4-D-Torus darstellt! Aus Abb. 42 wird ersichtlich, daß der obige Torus im Verhältnis zum 4-D-Modell wie der Querschnitt einer Kreisscheibe zum 3-D-Torus steht.
Sind bei einem Teilchen alle drei Spins gleichgerichtet, so addieren sie sich zu 3/2 und da es dann auch keine Rotation der Zwischenschichten gibt, wird der Isospin Null, wie man beim Omega¯-Teilchen sieht.
Lagert man an einem Proton zusätzlich ein Elektron an, verschwindet nach außen hin die Ladung, weil sich die überlagernden Effekte der entgegengesetzten Drehungen +L(p) und -L(e) aufheben . Die Spins sind parallel laufend und entgegensetzt gerichtet. Die Kopplungsschicht dazwischen hat demnach keine Drehung um die L-Achse und ist elektrisch neutral.

Es ist das Antiteilchen des Neutrinos, welches vom Elektron abgeleitet ist. Nach außen erscheint nun diese Teilchenkombination elektrisch neutral und wurde dementsprechend 'Neutron' genannt . Schaut man in die Mesonen-Tabelle, so sieht man, daß die geladenen Teilchen etwas schwerer sind, als die ungeladenen, weil sie zusätzlich noch die Ladungsenergie tragen. Das Neutron macht da keine Ausnahme, es trägt sogar zwei Ladungsteile, den positiven des Protons und den negativen des Elektrons. Aber da diese Ladungen sich innerlich aufheben, erscheint das Teilchen nach außen ungeladen. Erst beim Zerfall in die drei ursprünglichen Partikel wird der Ladungsanteil an der Energie deutlich.

Ein grundlegender Unterschied besteht jedoch zwischen dem Proton und dem Elektron. Während das letztere einen reinen Raumenergiewirbel darstellt, hat das Proton wahrscheinlich einen kondensierten Energiekern der Art, wie er oben im Abschnitt über Massebildung beschrieben wurde. Die Gesamtenergie des Protons ist dann die Summe aus der Energie des Kerns aus verdichteter Energie und der Energie in Torusform, welche eine Hülle um diesen Kern bildet.
Die Frage ist, warum Protonen eine so lange Lebenszeit haben. Schaut man sich die Quarkschichtung an, welche aus Energieschwingungen bestehen, so stehen diese Frequenzen mit dem Spin im Verhältnis von 3 zu 2. Dieses Verhältnis findet man auch bei Gravitationsresonanzen im Asteroidengürtel. Normalerweise ordnen sich entsprechend der Verteilung der wechselnden Kräfte Massebruchstücke an gewissen Orten an, wo wenig Wechsel stattfinden und meiden solche mit vielen Wechseln. Diese Lücken findet man in der Astronomie vorwiegend bei Resonanzverhältnissen der Werte 2:1, 3:1, 4:1, 5:2 und 7:2. Eine Ausnahme bildet 3:2, wo man im Asteroidengürtel die 'Hilda-Gruppe' vorfindet, was zeigt, daß die 3:2 Resonanz etwas besonderes an sich haben muß.
Um das Spezielle der 3:2 Resonanz herauszufinden, bauten STEWARD, APPLEGATE, DOUGLAS, GÜRSEL und SUSSMAN einen speziellen Computer (Digital Orrery), der das Sonnensystem von 100 Millionen Jahren aus der Vergangenheit bis in 110 Millionen Jahren in die Zukunft berechnete. Das Ergebnis: die 3:2 Resonanz ist stabil und nicht chaotisch! "Mathematisch gesehen, ist jede Resonanz ein spezielles Biest mit seinen eigenen Eigenschaften. Es gibt keinen Grund, warum die 3:2 Resonanz sich wie die 3:1 oder 2:1 verhalten soll, wie auch die Zahl 3/2 ungleich 3 und 2 ist. Offensichtlich ist die effektive Abwesenheit von Chaos eine der auffälligen Aspekte der 3:2 Resonanz."
Wahrscheinlich ist es gerade die 3:2 Resonanz der Torushülle, welche dem Proton die lange Lebensdauer gibt. Das Neutron hat schon 2 Schichten mehr (das Antineutrino und das Elektron) weshalb die Lebensdauer kürzer ist und ca 15 Minuten beträgt.
Zusammengehalten werden die Masseteilchen in einem Atom mit einiger Wahrscheinlichkeit durch den doppelten Trichter der Mitte des Toruswirbels, der auch die Reichweite dieser 'Starken Kernkraft' bestimmt. Als Analogie kann man sich verschiedene Trichter vorstellen, die ineinandergesteckt werden. 'Automatisch' werden die Spitzen der Trichter auf einer Linie zu liegen bekommen, egal wie weit man sie von der Mitte weg eingeführt hat, mit der Bedingung, daß sich die Spitze zumindest irgendwo innerhalb des Randes bewegt. Auch die Trennung ist dann schwieriger, da zuerst der Anstieg des Trichterrandes überwunden werden muß.
-
nicole6

- ModeratorIn

- Beiträge: 2333
- Registriert: 11.09.2009, 13:01
- Wohnort: München
- Ich bin: ehemalige SexarbeiterIn
RE: Diskussionspapier: Modell für Zeit und Raum
(der folgende Punkt ist für mich einer der wichtigsten Ergebnissen
dieses Modells, denn bisher gibt es keine Herleitung der Gravitationsformel!
Aber mit der Annahme eines 4-dimensionalen
Raumes ist es möglich, wie ich hier zeige)
19. GRAVITATION.
Das Phänomen von Gravitation ist immer noch eines der großen Rätsel der Wissenschaft. Solange man einen 3-D-Raum als obere Grenze annimmt, kommt man auch auf keine Lösung. Aber mit der Hypothese der Existenz des 4-D, von dem der einsichtbare 3-D ein Teil davon ist, findet man nicht nur eine Erklärung, sondern kann die Formel der Gravitation direkt aus dieser Annahme ableiten (Siehe Anhang). Hier ist auch der Fehler von RICHARD FEYNMANs Überlegung, bei der er die Summierung vieler kleiner Impulse als Ursache für Gravitationswirkung verwarf . Er ging von einer Schwingung im 3-D aus, und hier stimmt seine Argumentation, aber mit der Annahme des 4-D stimmt sie nicht mehr, dann wirken die Impulse auch von innen auf die Masseteilchen und heben so die Effekte nach außen auf.
Weiter oben wurde die Hypothese der Matrixschwingung aufgestellt. In der Feinstruktur des Raumes gehe ich von den Folgerungen der Quantengeometrodynamik (QGMD) aus, die besagt, daß im submikroskopischen Bereich der Raum zwischen verschiedenen schaumartigen Strukturen resoniert. "Die konjugierten Variablen sind hier die 'innere Krümmung' des dreidimensionalen Raumes und die 'äußere Krümmung', die angibt, wie dieser Raum relativ zu einer ihn umhüllenden 4-dimensionalen Geometrie gebogen ist. Beide dynamische Größen können nicht gleichzeitig verschwinden, ohne HEISENBERGs Unschärferelation zu verletzen. Daher ist der Raum in der Größenordnung der Quantenlängen der Ort lebendigster Geometrodynamik, wie auch dort die elektromagnetischen Feldgrößen lebhaftesten Schwankungen unterworfen sind."
Als Analogie kann man sich eine stark bewegte Wasserfläche vorstellen, auf der die Wellen von allen Seiten kommen und gehen. Nun stellen wir uns ein Stück 3-D-Raum vor, in dem sich ein einzelnes Masseobjekt befindet, z.B. nur die weiße Kugel in Abb. 44.
Vom 4-D aus ist nicht nur die Oberfläche sichtbar, sondern auch jedes einzelne Atom liegt vom 4-D-Raum aus offen da, wie vom 3-D aus die Projektion der Objekte auf den 2-D das Innere der Kreise erkennen läßt! Die Kräfte der Quantenschwankungen wirken also nicht nur von allen Seiten auf das Objekt, sondern auch von Innen in jede Richtung! Zum Zusammenhang der Schwankungen mit der Raumenergie setzt JOHN ARCHIBALD WHEELER für die QGMD folgende Behauptung auf: (Krümmung)=(Dichte der Masse-Energie) .
Die Geschwindigkeiten der Quantenschwankungen sind sicher unterschiedlich. Durch ihre große Anzahl kann man statistisch eine mittlere Geschwindigkeit bestimmen, der man den Wert v zuschreibt. Nun bringen wir eine zweite Kugel (T2) in den Proberaum, in Abb. 44 ist es die dunkle. Sie schwächt das Feld der Quantenschwankungen zwischen den Objekten, die sich somit aufeinander zu bewegen. Als allgemeinen Fall muß man annehmen, daß beide Objekte relative Geschwindigkeiten zueinander haben. Dann kann man eines als Nullpunkt für die Koordinaten wählen, z.B. die weiße Kugel (T1), und die Geschwindigkeitsänderung der anderen relativ dazu berechnen. Die Kraft der Schwächung des Quantenfelds bewirkt eine Zentripedalbeschleunigung der dunklen Kugel zur weißen hin (Abb. 45).
Im Prinzip hat LEIBNITZ die Idee von Gravitation aus Stroßprozessen vorweggenommen, als er im 5. Brief an NEWTON's Vertreter CLARKE schrieb: Denn es ist eine sonderbare Fiktion, wenn man der ganzen Materie Schwere zuschreibt; und sogar Richtung auf jede andere Materie, als zöge jeder Körper in gleicher Weise jeden anderen Körper im Verhältnis der Massen und der Entfernung an; und das mit einer Anziehung im eigentlichen Sinne, die nicht einem verborgenen Stoßprozeß in den Körpern entstammt ... Ein Körper wird natürlicherweise nie anders als durch einen anderen Körper in Bewegung versetzt, der ihn durch Berührung stößt; und danach bleibt er in Bewegung, bis er durch einen anderen Körper, der ihn berührt, gehindert wird. Jede andere Einwirkung auf Körper ist entweder ein Wunder oder eine Einbildung."
Zuerst stellt man die Proportionalitäten klar. Die resultierende Kraft Fres (durch die Abschirmung) ist relativ zur mittleren Kraft Fm (der erzeugenden Impulse) gegeben. Fm läßt sich dabei durch die Dichte der Feldlinien darstellen. Erhöht man nun diese Energiedichte von Fm , unter der Voraussetzung sonst alles gleich zu lassen, so erniedrigt sich dabei das Verhältnis mit Fres. In Kurzschrift: Fm ~ 1/Fres, oder umformuliert
Fres ~ 1/Fm. (1)
Dann ist offensichtlich Fres auch mit F1 und F2 proportional, da Fres steigt, wenn F1 oder F2 steigt. In Formelschrift:
Fres ~ F1 und Fres ~ F2
Zusammengefaßt ergibt dies mit einer Proportionalkonstanten k:
Fres = k F1F2 /Fm . (1)
Mit m1 für die Masse von T1 und m2 für die Masse von T2 muß man für einen momentanen Abstand R der Massen m1 und m2 die Kräfte der Zentripedalbeschleunigung einsetzen, und erhält mit v als mittlere Geschwindigkeit der Quantenschwankungen des Feldes:
F1 = m1v²/R und F2 = m2v²/R (2)
(2) in (1) eingesetzt ergibt dann:
Fres. = km1m2v4/FmR² (3).
Nun faßt man in (3) die konstanten Werte zusammen und setzt für kv4/Fm die Konstante K. Die Einheiten von K sind: [m4s2/s4m kg] = [m3/s2kg]. und aus (3) wird
Fres. = Km1m2/R² (4)
Die Gleichung (4) hat genau die Form, und die Konstante K hat exakt die Einheiten der Gravitationsgleichung.
In diesen Überlegungen ist als Grundannahme der Zusammenhang von Quantenschwankungen mit Resonanzschwingungen des Raumes vorausgesetzt. Dies könnte eventuell zu einer Technik führen, die Antigravitation erzeugt. Man müßte ein Gerät erfinden, was genau in der mittleren Frequenz der Quantenschwingungen Energiewellen erzeugt. Diese würden dann die Abschwächung des Feldes zwischen zwei Körpern wieder aufheben, und bei entsprechender Stärke könnte der Apparat schweben, weil dann die Gravitation aufgehoben wäre.
20. TRÄGHEITSMOMENT
Bisher gibt es keine Erklärung für das 'Trägheitsgesetz' und für den Zusammenhang von Masse und Trägheitsmoment. Angeblich sollen Objekte, auf die keine Kraft wirkt, entweder ruhen oder sich gleichförmig geradeaus bewegen. In dieser Formulierung ist das 'Trägheitsgesetz' allerdings falsch. Wenn es nur ein einziges Objekt im Universum gäbe, könnte man auch nicht von 'Geschwindigkeit' sprechen, der Begriff wäre vollkommen sinnlos. Hat man allerdings mindestens 2 Objekte, so muß auf sie mindestens 1 Kraft wirken, die Gravitation. Dann aber bewegen sie sich unbehindert nicht auf Geraden, sondern auf Spiralen, egal ob die Kraft zwischen beiden linear, quadratisch oder in einer höheren Potenz ist. Um auf einer 'Geraden' zu laufen, braucht es einer weiteren Kraft, die genau diese Spiralbahn verhindert! Es gibt auch nirgends im Universum irgend eine Beobachtung die darauf hinweist, daß ein Objekt sich 'geradlinig' bewegt. Es kann auch nie ein Zustand geben, in dem keine Kraft auf das Objekt wirkt, da die Schwerkraft beliebig weit wirkt.
Wie ich schon im oberen Abschnitt erläuterte, wirken die Quantenschwankungen des Raumes von der vierten Dimension aus auf die Massekörper. Da vom 4-D aus das Innere der Körper so offen daliegt wie für uns im 3-D das Innere eines Kreises, so gleichen sich die Stöße der Quantenschwankungen aus, egal ob das Objekt sich im 3-D bewegt oder ob es ruht (Abb. 46).
Das Gleichgewicht des Drucks durch die Quantenschwankungen ist dynamisch. Wenn es Betragsänderungen der Geschwindigkeitsimpulse von Quantenschwankungen des Raumes gibt, dann liegen sie, wie ich weiter oben schon zeigte, in einer neuen Dimension. Dies entspricht einer Bewegung im rechten Winkel zum 3-D. Erst jetzt zeigt sich ein Effekt, den man von Objektbewegungen in Luft oder Wasser kennt. Der Unterschied ist allerdings, daß der Luftwiderstand von der Oberfläche des Objekts abhängt, der Widerstand gegen Beschleunigungen von allen Masseteilchen des Objekts.
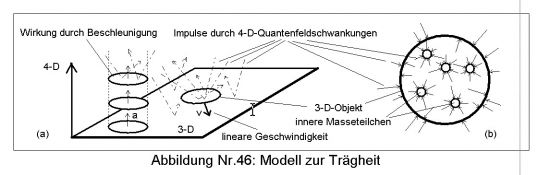
RICHARD FEYNMAN wunderte sich, ob das Gravitationsgesetz wirklich ein fundamentales Gesetz sei. Offensichtlich ist es ein abgeleitetes, wie ich oben zeigte. Da FEYNMAN die Ursache im 3-D suchte , konnte er auf keine Lösung kommen. Die Idee, Gravitation aus den Stößen von 'feiner Materie' her zu erklären, schlug 1888 LESAGE vor, was POINCARÉ zur Aussage veranlaßte: "Und wie steht es mit dem Newtonschen Gesetze selbst? Seine so lange verborgene Einfachheit ist vielleicht nur scheinbar. Wer kann wissen, ob sie nicht aus irgend einem komplizierten Mechanismus entsteht, aus dem Stoße irgend einer feinen unregelmäßig bewegten Materie, und ob sie nicht durch das Spiel der Mittelwerte und großen Zahl einfach wurde? Auf jeden Fall ist es schwierig, nicht vorauszusetzen, daß das wirkliche Gesetz ergänzende Glieder enthält, welche für kleine Entfernungen merkbar werden können."
(Jetzt kommt eine Analyse der Relativitätstheorie von Einstein,
und deren vielen Fehlern darin. Das lasse ich hier aber weg,
da es die Sache nur am Rand berührt.)
23. HENKELTOPOLOGIE UND SCHWACHE WECHSELWIRKUNG.
Um die folgende Skizze richtig zu interpretieren, muß ich nochmals daran erinnern, daß sich das Geschehen im 4-D abspielt. Auf einer Kugel sind viele Kreisumfänge simultan möglich, auf der Dimension darunter erscheint davon im Schnitt nur 1 Kreis. Der Schnitt eines 4-D-Torus erscheint im 3-D von außen als 1 Sphäre auch wenn im Original viele Teil-Torusformen darauf Platz haben. Die beiden getrennt gezeichnete Torusformen breiten sich in Wirklichkeit auf dem gesamten Umfang der Elektronenschicht aus.
Als Konvention treffen wir nun folgende Regeln: Die Drehung im Uhrzeigersinn der Hauptachse des Torus entspreche der positiven Ladung (L3), die im Gegenuhrzeigersinn der negativen Ladung (L1 und L2). Elektronen können sich paarweise auf einer Bahn nur mit antiparallelem Spin aufhalten. Also muß ein Spin nach oben (S1), der andere nach unten (S2) zeigen. Die Resultierenden (R1, R2 und R3) sind in der Abbildung mit einem dicken Pfeil eingezeichnet. Nimmt man nun eine energetische 'Henkel-Brücke' zwischen den Elektronen und dem Kern an, so können sie sich nur auf der in Abb. 49 gezeichneten Weise bilden.
Durch den Energiefluß des Kernspins muß ein linkshändiges Elektron oben und das rechtshändige unten andocken. Der Übersichtlichkeit halber wurde die Energiekopplung der Elektronen untereinander weggelassen. Solche torusartigen Kopplungsschläuche sind nichts ungewöhnliches in der Natur. Im dreidimensionalen Bereich kennt man sie bei Tornados. Übersteigt die Energiedifferenz zwischen zwei Schichten ein gewisses Maß , so läßt die geringste Störung der Grenzschicht die Trombe entstehen. Diese bewegt sich dann nicht wie ein aufrollender Elefantenrüssel zum Boden, sondern eher wie eine Teleskopantenne . Möglicherweise ist im Prinzip der gleiche Kopplungsmechanismus zwischen einem andockenden Elektron und dem Atomkern wirksam.
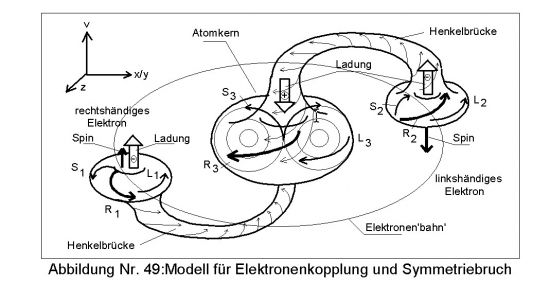
Nun, wie könnte man diese Topologie in einem Experiment nachweisen? Wie man sieht, haben aufgrund der Torusform des Kernspins die Ankopplungen der Elektronen verschiedenen Durchmesser. In Abb. 49 ist am Kern der untere Kopplungsschlauch dünner als der obere, weil er von innen an den rotierenden Torus ankoppelt. Nun soll die Annahme gelten, daß die Stärke der Kopplung proportional zur Energiedichte sei. Wenn man nun in einem starken Magnetfeld alle Spins parallel ausrichtet, dann ist damit die Wahrscheinlichkeit höher, daß bei einem Zerfall der obere Henkel des linkshändigen Elektrons abreißt, weil er eine geringere Energiedichte hat als der untere.
Dieser Versuch wurde 1956 von Frau WU und ihren Mitarbeitern an der Columbia Universität in New York gemacht. Kobaltatome wurden in einem Magnetfeld so ausgerichtet, daß alle Drehachsen parallel waren. Dann beobachtete man den Zerfall des Kobaltisotops 60 in Nickel, was dabei noch ein Elektron und ein Antineutrino abschickt. Da sich die Topologie von Abb. 49 im 4-D befindet, der auf allen Richtungen des 3-D senkrecht steht, hat die Ausrichtung des Magnetfeldes im 3-D keinen Einfluß auf die Asymmetrie der topologischen Kopplung der Elektronen im 4-D. Das Ergebnis des Versuchs war ein Symmetriebruch: es wurden ca 30% mehr linkshändige Elektronen abgeschickt .
(Der folgende Abschnitt, die Analyse des Kreiseleffekts, war
für mich der eigentliche Anlass mich tiefer in das Thema
einzuarbeiten, und eine widerspruchsfreie Erklärung zu finden,
denn die offizielle, die in allen Physikbüchern steht, ist schlicht
und einfach falsch!)
22. KREISELMOMENT.
Vom Kreisel gibt es eine Menge Beschreibungen, aber bisher fand ich noch keine Erklärung. Warum kippt ein drehender Kreisel nicht um, ein stillstehender aber schon? An der Schwerkraft kann es nicht liegen, denn durch eine liegende Anordnung (Abb. 50) kann man ihren Effekt auf die Richtungsstabilität der Drehachse ausschalten. Das Trägheitsmoment kann es auch nicht sein, denn es wirkt symmetrisch zur Drehachse und alle Vektoren gleichen sich zu Null aus. Es muß eine Kraft sein, welche von den bisher bekannten unabhängig ist, denn sie erzeugt ein Drehmoment, welches zu den anderen Kräften rechtwinklig steht.
Die Scheibe in Abb. 92 ist auf einem allseitig drehbaren Lager durch ein Ausgleichsgewicht so ausbalanciert, daß die Drehachse gerade waagerecht liegt. Bei stillstehender Scheibe kippt die Achse einfach nach links unten, wenn man das Gewicht K auf den Waageteller legt. Rotiert jedoch die Scheibe, dann geschieht etwas völlig anderes. Dreht sie sich im angegebenen Sinn der Abb. 50 nach rechts, dann kippt die Achse nicht mehr nach unten, sondern beginnt sich im Gegenuhrzeigersinn zu drehen. Würde sich die Scheibe nach links drehen, wäre die Rotationsrichtung des Systems im Uhrzeigersinn. Bis hierher sind dies Beschreibungen.
Wie kann man es erklären? Die Gravitation erklärte ich weiter oben durch Quantenschwankungen des vierdimensionalen Raumes im Sinn der QGMD. Lineare Bewegungen werden dadurch nicht beeinflußt, da vom 4-D aus die Kräfte auch von innen auf die 3-D-Objekte wirken.
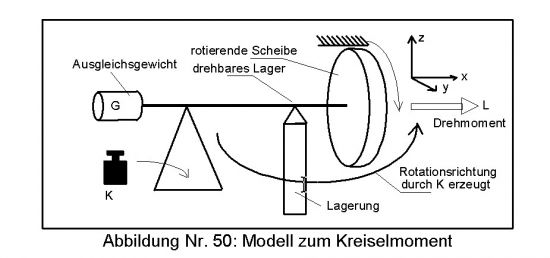
Beschleunigungen jedoch führen zu einer Änderung der mittleren Impulsrate der Quantenschwankungen des Raumes, worauf die Trägheit zurückzuführen ist. Der gleiche Effekt wirkt in diesem Fall. Vom 3-D-Raum aus steht die vierte Raumdimension senkrecht auf allen drei Dimensionen. Wenn sich der Kreisel dreht, führt also jede Neigung der Drehachse zu einer Impulsänderung in Richtung des 4-D, weshalb der Kreisel stabil bleibt. Legt man im obigen Fall von Abb. 50 ein zusätzliches Gewicht auf die Drehachse, so wirkt es in Richtung -z mit einer Kraft des Rades in Richtung +z. Vom 4-D aus wirken nun auf jedes einzelne Atom des Rades vom 4-D aus die Quantenimpulse und drücken das Rad nach unten. Durch die Rotation selbst hat dies einen Effekt, als ob das Rad von oben in Kontakt mit einer Platte kommt, wie es Abb. 50 zeigt. Bei anderer Drehrichtung ist der Effekt eben umgekehrt. Nach meiner Einschätzung ist dies einer der überzeugendsten Beweise für die Existenz der Wirkungen von Quantenschwankungen des vierdimensionalen Raumes auf Objekte des 3-D.
23. TOPOLOGIE DES MAGNETISMUS.
Im oberen Abschnitt wurden das elektrische Feld mit der Topologie eines Henkels beschrieben. Die Form selbst wird dabei aus der Raumenergie gebildet. An den Rändern dieser henkelförmigen Wirbel werden weitere Raumenergieteilchen mitgerissen und bilden einen Wirbelschlauch, ähnlich einem Tornado, dessen Wirkung mit dem Abstand schnell abnimmt.
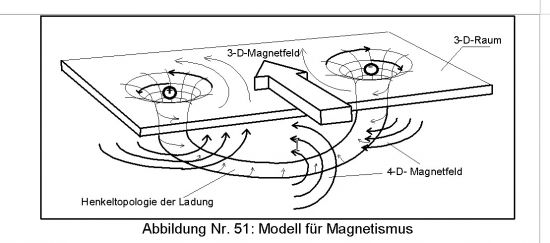
In Abb. 51 ist die Situation skizziert. Die torusförmigen Ladungsträger sind hier der Einfachheit halber mit '+' und '-' symbolisiert. Der Schlauch entspricht einem Henkel der Art von Abb. 49. Aus der Rotationsrichtung des vierdimensionalen Schlauches ergibt sich konsequenterweise die Rotationsrichtung der vierdimensionalen Wirbelbildung.
Im 3-D erscheint nur noch die Projektion dieser Wirbel mit dem Effekt der unter 'Magnetismus bekannt ist. Somit ist klar, daß es keine Monopole von Magneten geben kann, aber einzelne elektrische Ladungen.
Im Neutron heben sich die Rotationen um die Hauptachse des Torus auf, da der überlagerte Elektrontorus die Drehung in Gegenrichtung hat. Was sich nicht aufhebt, ist die Drehung um die Schlauchachse, welche das magnetische Moment des Neutrons beibehält. Ein Elektron hat keinen kondensierten Kern wie ein Proton und stellt einen reinen Wirbel aus Raumenergie dar, weshalb das magnetische Moment auch entsprechend stark ist .
24. DER 'TUNNELEFFEKT' UND DIE 'STARKE KERNKRAFT'.
In einem Atomkern werden die Teilchen durch die 'Starke Kernkraft' zusammengehalten, welcher ich im vorigen Abschnitt die topologische Form eines Torus gab. Im dreidimensionalen Raum kann man sich den Potentialtrichter als einen Vulkanschlund vorstellen. Solange sich ein Teilchen im inneren Schlund befindet, kann es dem Vulkan nicht 'den Buckel 'runter rutschen'. Doch wenn es auch nur wenig über dem Rand ist, entfernt es sich unaufhörlich vom Kegelrand. Normalerweise hat aber ein Teilchen nicht genug Energie um über die Barriere zu springen, denn sonst wäre es nicht mehr darin. Innerhalb des von mir vorgeschlagenen Modells befindet sich aber der 3-D-Raum in ständigem Schwingungszustand und da kann es geschehen, daß solch ein Raumschwingung (K) zu dem Zeitpunkt an einem Atom vorbeikommt, an dem ein Teilchen im Potentialtrichter sich gerade nach oben bewegt (Abb. 52a).
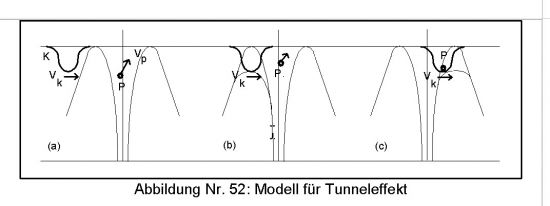
Die Raumschwingung erniedrigt bei der Ankunft eine Seite des Trichters (b). Wenn nun bei der Passage des Schlundes das Teilchen sich gerade auf dem Umkehrpunkt der Bewegung befindet, dann kann es von der Raumschwingung aufgenommen und nach außen getragen werden (c). In diesem Modell braucht sich das Teilchen keine 'Energie von der HEISENBERGschen Unschärferelation zu leihen', wie bisher der Effekt erklärt wird . Das klingt, als ob die Wortbildung der Forscher eine reale Institution wäre, wie das Elektrizitätswerk oder eine Bank.
25. DIE 'WECHSELWIRKUNG DES NEUTRALEN STROMES’.
Wenn ein Elektron auf Materie trifft, ändert es zwar seine Energie und den Impuls, bleibt aber ein Elektron. Von Neutrinos, die elektrisch neutral sind, kennt man den Effekt, daß sie sich beim Zusammenstoß in ein geladenes Teilchen (Lepton) verwandeln. Doch man fand auch Reaktionen, bei denen dies nicht stattfand. Man benannte den Effekt: Wechselwirkung des neutralen Stromes.
Mit Hilfe der Topologie des Torus läßt sich dieser Effekt erklären. Ein Neutrino hat nur eine Rotation um die Schlauchachse des Torus und keine um die Zentralachse, weshalb es keine Ladung trägt.
Wenn es nun auf einen 4-D-Torus eines Masseteilchens stößt, dann bekommt der Torus des Neutrinos einen Drehimpuls um die Zentralachse, was sich nach außen als Ladung zeigt. In Ab. 96 entspricht dies der Bahn 2. Trifft das Neutrino jedoch im rechten Winkel auf den Teilchentorus, dann bekommt der Drehimpuls der Schlauchachse keine Überlagerung und die neutrale Ladung bleibt erhalten. Da sich das Ganze in quantisierten Systemen abspielt, gibt es vom rechten Winkel aus eine gewisse zulässige Breite der Abweichung, innerhalb der noch kein Ladungsimpuls erzeugt wird.
(Nun, als nächstes muss ich eine Selektion treffen und sie
auf Englisch übersetzen. Die Arbeit hier ist zu lang und zu
ausführlich für eine Veröffentlichung in einer Fachzeitschrift.
Ich werde auch nicht alles Wissen auf einmal herzeigen.
Ich lies hier auch die Zitierreferenzen weg.
Morgen werde ich noch eine kurze Abhandlung zu den
gravierenden Fehlern in Einsteins Theorie zur Relativität hochladen.
Ihr braucht davor nicht zurück zu schrecken!
Die Fehler sind so offensichtlich und gravierend, dass das
Wissen eines normalen Schulabschlusses ausreicht um die Sache
zu verstehen!)
dieses Modells, denn bisher gibt es keine Herleitung der Gravitationsformel!
Aber mit der Annahme eines 4-dimensionalen
Raumes ist es möglich, wie ich hier zeige)
19. GRAVITATION.
Das Phänomen von Gravitation ist immer noch eines der großen Rätsel der Wissenschaft. Solange man einen 3-D-Raum als obere Grenze annimmt, kommt man auch auf keine Lösung. Aber mit der Hypothese der Existenz des 4-D, von dem der einsichtbare 3-D ein Teil davon ist, findet man nicht nur eine Erklärung, sondern kann die Formel der Gravitation direkt aus dieser Annahme ableiten (Siehe Anhang). Hier ist auch der Fehler von RICHARD FEYNMANs Überlegung, bei der er die Summierung vieler kleiner Impulse als Ursache für Gravitationswirkung verwarf . Er ging von einer Schwingung im 3-D aus, und hier stimmt seine Argumentation, aber mit der Annahme des 4-D stimmt sie nicht mehr, dann wirken die Impulse auch von innen auf die Masseteilchen und heben so die Effekte nach außen auf.
Weiter oben wurde die Hypothese der Matrixschwingung aufgestellt. In der Feinstruktur des Raumes gehe ich von den Folgerungen der Quantengeometrodynamik (QGMD) aus, die besagt, daß im submikroskopischen Bereich der Raum zwischen verschiedenen schaumartigen Strukturen resoniert. "Die konjugierten Variablen sind hier die 'innere Krümmung' des dreidimensionalen Raumes und die 'äußere Krümmung', die angibt, wie dieser Raum relativ zu einer ihn umhüllenden 4-dimensionalen Geometrie gebogen ist. Beide dynamische Größen können nicht gleichzeitig verschwinden, ohne HEISENBERGs Unschärferelation zu verletzen. Daher ist der Raum in der Größenordnung der Quantenlängen der Ort lebendigster Geometrodynamik, wie auch dort die elektromagnetischen Feldgrößen lebhaftesten Schwankungen unterworfen sind."
Als Analogie kann man sich eine stark bewegte Wasserfläche vorstellen, auf der die Wellen von allen Seiten kommen und gehen. Nun stellen wir uns ein Stück 3-D-Raum vor, in dem sich ein einzelnes Masseobjekt befindet, z.B. nur die weiße Kugel in Abb. 44.
Vom 4-D aus ist nicht nur die Oberfläche sichtbar, sondern auch jedes einzelne Atom liegt vom 4-D-Raum aus offen da, wie vom 3-D aus die Projektion der Objekte auf den 2-D das Innere der Kreise erkennen läßt! Die Kräfte der Quantenschwankungen wirken also nicht nur von allen Seiten auf das Objekt, sondern auch von Innen in jede Richtung! Zum Zusammenhang der Schwankungen mit der Raumenergie setzt JOHN ARCHIBALD WHEELER für die QGMD folgende Behauptung auf: (Krümmung)=(Dichte der Masse-Energie) .

Die Geschwindigkeiten der Quantenschwankungen sind sicher unterschiedlich. Durch ihre große Anzahl kann man statistisch eine mittlere Geschwindigkeit bestimmen, der man den Wert v zuschreibt. Nun bringen wir eine zweite Kugel (T2) in den Proberaum, in Abb. 44 ist es die dunkle. Sie schwächt das Feld der Quantenschwankungen zwischen den Objekten, die sich somit aufeinander zu bewegen. Als allgemeinen Fall muß man annehmen, daß beide Objekte relative Geschwindigkeiten zueinander haben. Dann kann man eines als Nullpunkt für die Koordinaten wählen, z.B. die weiße Kugel (T1), und die Geschwindigkeitsänderung der anderen relativ dazu berechnen. Die Kraft der Schwächung des Quantenfelds bewirkt eine Zentripedalbeschleunigung der dunklen Kugel zur weißen hin (Abb. 45).

Im Prinzip hat LEIBNITZ die Idee von Gravitation aus Stroßprozessen vorweggenommen, als er im 5. Brief an NEWTON's Vertreter CLARKE schrieb: Denn es ist eine sonderbare Fiktion, wenn man der ganzen Materie Schwere zuschreibt; und sogar Richtung auf jede andere Materie, als zöge jeder Körper in gleicher Weise jeden anderen Körper im Verhältnis der Massen und der Entfernung an; und das mit einer Anziehung im eigentlichen Sinne, die nicht einem verborgenen Stoßprozeß in den Körpern entstammt ... Ein Körper wird natürlicherweise nie anders als durch einen anderen Körper in Bewegung versetzt, der ihn durch Berührung stößt; und danach bleibt er in Bewegung, bis er durch einen anderen Körper, der ihn berührt, gehindert wird. Jede andere Einwirkung auf Körper ist entweder ein Wunder oder eine Einbildung."
Zuerst stellt man die Proportionalitäten klar. Die resultierende Kraft Fres (durch die Abschirmung) ist relativ zur mittleren Kraft Fm (der erzeugenden Impulse) gegeben. Fm läßt sich dabei durch die Dichte der Feldlinien darstellen. Erhöht man nun diese Energiedichte von Fm , unter der Voraussetzung sonst alles gleich zu lassen, so erniedrigt sich dabei das Verhältnis mit Fres. In Kurzschrift: Fm ~ 1/Fres, oder umformuliert
Fres ~ 1/Fm. (1)
Dann ist offensichtlich Fres auch mit F1 und F2 proportional, da Fres steigt, wenn F1 oder F2 steigt. In Formelschrift:
Fres ~ F1 und Fres ~ F2
Zusammengefaßt ergibt dies mit einer Proportionalkonstanten k:
Fres = k F1F2 /Fm . (1)
Mit m1 für die Masse von T1 und m2 für die Masse von T2 muß man für einen momentanen Abstand R der Massen m1 und m2 die Kräfte der Zentripedalbeschleunigung einsetzen, und erhält mit v als mittlere Geschwindigkeit der Quantenschwankungen des Feldes:
F1 = m1v²/R und F2 = m2v²/R (2)
(2) in (1) eingesetzt ergibt dann:
Fres. = km1m2v4/FmR² (3).
Nun faßt man in (3) die konstanten Werte zusammen und setzt für kv4/Fm die Konstante K. Die Einheiten von K sind: [m4s2/s4m kg] = [m3/s2kg]. und aus (3) wird
Fres. = Km1m2/R² (4)
Die Gleichung (4) hat genau die Form, und die Konstante K hat exakt die Einheiten der Gravitationsgleichung.
In diesen Überlegungen ist als Grundannahme der Zusammenhang von Quantenschwankungen mit Resonanzschwingungen des Raumes vorausgesetzt. Dies könnte eventuell zu einer Technik führen, die Antigravitation erzeugt. Man müßte ein Gerät erfinden, was genau in der mittleren Frequenz der Quantenschwingungen Energiewellen erzeugt. Diese würden dann die Abschwächung des Feldes zwischen zwei Körpern wieder aufheben, und bei entsprechender Stärke könnte der Apparat schweben, weil dann die Gravitation aufgehoben wäre.
20. TRÄGHEITSMOMENT
Bisher gibt es keine Erklärung für das 'Trägheitsgesetz' und für den Zusammenhang von Masse und Trägheitsmoment. Angeblich sollen Objekte, auf die keine Kraft wirkt, entweder ruhen oder sich gleichförmig geradeaus bewegen. In dieser Formulierung ist das 'Trägheitsgesetz' allerdings falsch. Wenn es nur ein einziges Objekt im Universum gäbe, könnte man auch nicht von 'Geschwindigkeit' sprechen, der Begriff wäre vollkommen sinnlos. Hat man allerdings mindestens 2 Objekte, so muß auf sie mindestens 1 Kraft wirken, die Gravitation. Dann aber bewegen sie sich unbehindert nicht auf Geraden, sondern auf Spiralen, egal ob die Kraft zwischen beiden linear, quadratisch oder in einer höheren Potenz ist. Um auf einer 'Geraden' zu laufen, braucht es einer weiteren Kraft, die genau diese Spiralbahn verhindert! Es gibt auch nirgends im Universum irgend eine Beobachtung die darauf hinweist, daß ein Objekt sich 'geradlinig' bewegt. Es kann auch nie ein Zustand geben, in dem keine Kraft auf das Objekt wirkt, da die Schwerkraft beliebig weit wirkt.
Wie ich schon im oberen Abschnitt erläuterte, wirken die Quantenschwankungen des Raumes von der vierten Dimension aus auf die Massekörper. Da vom 4-D aus das Innere der Körper so offen daliegt wie für uns im 3-D das Innere eines Kreises, so gleichen sich die Stöße der Quantenschwankungen aus, egal ob das Objekt sich im 3-D bewegt oder ob es ruht (Abb. 46).
Das Gleichgewicht des Drucks durch die Quantenschwankungen ist dynamisch. Wenn es Betragsänderungen der Geschwindigkeitsimpulse von Quantenschwankungen des Raumes gibt, dann liegen sie, wie ich weiter oben schon zeigte, in einer neuen Dimension. Dies entspricht einer Bewegung im rechten Winkel zum 3-D. Erst jetzt zeigt sich ein Effekt, den man von Objektbewegungen in Luft oder Wasser kennt. Der Unterschied ist allerdings, daß der Luftwiderstand von der Oberfläche des Objekts abhängt, der Widerstand gegen Beschleunigungen von allen Masseteilchen des Objekts.

RICHARD FEYNMAN wunderte sich, ob das Gravitationsgesetz wirklich ein fundamentales Gesetz sei. Offensichtlich ist es ein abgeleitetes, wie ich oben zeigte. Da FEYNMAN die Ursache im 3-D suchte , konnte er auf keine Lösung kommen. Die Idee, Gravitation aus den Stößen von 'feiner Materie' her zu erklären, schlug 1888 LESAGE vor, was POINCARÉ zur Aussage veranlaßte: "Und wie steht es mit dem Newtonschen Gesetze selbst? Seine so lange verborgene Einfachheit ist vielleicht nur scheinbar. Wer kann wissen, ob sie nicht aus irgend einem komplizierten Mechanismus entsteht, aus dem Stoße irgend einer feinen unregelmäßig bewegten Materie, und ob sie nicht durch das Spiel der Mittelwerte und großen Zahl einfach wurde? Auf jeden Fall ist es schwierig, nicht vorauszusetzen, daß das wirkliche Gesetz ergänzende Glieder enthält, welche für kleine Entfernungen merkbar werden können."
(Jetzt kommt eine Analyse der Relativitätstheorie von Einstein,
und deren vielen Fehlern darin. Das lasse ich hier aber weg,
da es die Sache nur am Rand berührt.)
23. HENKELTOPOLOGIE UND SCHWACHE WECHSELWIRKUNG.
Um die folgende Skizze richtig zu interpretieren, muß ich nochmals daran erinnern, daß sich das Geschehen im 4-D abspielt. Auf einer Kugel sind viele Kreisumfänge simultan möglich, auf der Dimension darunter erscheint davon im Schnitt nur 1 Kreis. Der Schnitt eines 4-D-Torus erscheint im 3-D von außen als 1 Sphäre auch wenn im Original viele Teil-Torusformen darauf Platz haben. Die beiden getrennt gezeichnete Torusformen breiten sich in Wirklichkeit auf dem gesamten Umfang der Elektronenschicht aus.
Als Konvention treffen wir nun folgende Regeln: Die Drehung im Uhrzeigersinn der Hauptachse des Torus entspreche der positiven Ladung (L3), die im Gegenuhrzeigersinn der negativen Ladung (L1 und L2). Elektronen können sich paarweise auf einer Bahn nur mit antiparallelem Spin aufhalten. Also muß ein Spin nach oben (S1), der andere nach unten (S2) zeigen. Die Resultierenden (R1, R2 und R3) sind in der Abbildung mit einem dicken Pfeil eingezeichnet. Nimmt man nun eine energetische 'Henkel-Brücke' zwischen den Elektronen und dem Kern an, so können sie sich nur auf der in Abb. 49 gezeichneten Weise bilden.
Durch den Energiefluß des Kernspins muß ein linkshändiges Elektron oben und das rechtshändige unten andocken. Der Übersichtlichkeit halber wurde die Energiekopplung der Elektronen untereinander weggelassen. Solche torusartigen Kopplungsschläuche sind nichts ungewöhnliches in der Natur. Im dreidimensionalen Bereich kennt man sie bei Tornados. Übersteigt die Energiedifferenz zwischen zwei Schichten ein gewisses Maß , so läßt die geringste Störung der Grenzschicht die Trombe entstehen. Diese bewegt sich dann nicht wie ein aufrollender Elefantenrüssel zum Boden, sondern eher wie eine Teleskopantenne . Möglicherweise ist im Prinzip der gleiche Kopplungsmechanismus zwischen einem andockenden Elektron und dem Atomkern wirksam.

Nun, wie könnte man diese Topologie in einem Experiment nachweisen? Wie man sieht, haben aufgrund der Torusform des Kernspins die Ankopplungen der Elektronen verschiedenen Durchmesser. In Abb. 49 ist am Kern der untere Kopplungsschlauch dünner als der obere, weil er von innen an den rotierenden Torus ankoppelt. Nun soll die Annahme gelten, daß die Stärke der Kopplung proportional zur Energiedichte sei. Wenn man nun in einem starken Magnetfeld alle Spins parallel ausrichtet, dann ist damit die Wahrscheinlichkeit höher, daß bei einem Zerfall der obere Henkel des linkshändigen Elektrons abreißt, weil er eine geringere Energiedichte hat als der untere.
Dieser Versuch wurde 1956 von Frau WU und ihren Mitarbeitern an der Columbia Universität in New York gemacht. Kobaltatome wurden in einem Magnetfeld so ausgerichtet, daß alle Drehachsen parallel waren. Dann beobachtete man den Zerfall des Kobaltisotops 60 in Nickel, was dabei noch ein Elektron und ein Antineutrino abschickt. Da sich die Topologie von Abb. 49 im 4-D befindet, der auf allen Richtungen des 3-D senkrecht steht, hat die Ausrichtung des Magnetfeldes im 3-D keinen Einfluß auf die Asymmetrie der topologischen Kopplung der Elektronen im 4-D. Das Ergebnis des Versuchs war ein Symmetriebruch: es wurden ca 30% mehr linkshändige Elektronen abgeschickt .
(Der folgende Abschnitt, die Analyse des Kreiseleffekts, war
für mich der eigentliche Anlass mich tiefer in das Thema
einzuarbeiten, und eine widerspruchsfreie Erklärung zu finden,
denn die offizielle, die in allen Physikbüchern steht, ist schlicht
und einfach falsch!)
22. KREISELMOMENT.
Vom Kreisel gibt es eine Menge Beschreibungen, aber bisher fand ich noch keine Erklärung. Warum kippt ein drehender Kreisel nicht um, ein stillstehender aber schon? An der Schwerkraft kann es nicht liegen, denn durch eine liegende Anordnung (Abb. 50) kann man ihren Effekt auf die Richtungsstabilität der Drehachse ausschalten. Das Trägheitsmoment kann es auch nicht sein, denn es wirkt symmetrisch zur Drehachse und alle Vektoren gleichen sich zu Null aus. Es muß eine Kraft sein, welche von den bisher bekannten unabhängig ist, denn sie erzeugt ein Drehmoment, welches zu den anderen Kräften rechtwinklig steht.
Die Scheibe in Abb. 92 ist auf einem allseitig drehbaren Lager durch ein Ausgleichsgewicht so ausbalanciert, daß die Drehachse gerade waagerecht liegt. Bei stillstehender Scheibe kippt die Achse einfach nach links unten, wenn man das Gewicht K auf den Waageteller legt. Rotiert jedoch die Scheibe, dann geschieht etwas völlig anderes. Dreht sie sich im angegebenen Sinn der Abb. 50 nach rechts, dann kippt die Achse nicht mehr nach unten, sondern beginnt sich im Gegenuhrzeigersinn zu drehen. Würde sich die Scheibe nach links drehen, wäre die Rotationsrichtung des Systems im Uhrzeigersinn. Bis hierher sind dies Beschreibungen.
Wie kann man es erklären? Die Gravitation erklärte ich weiter oben durch Quantenschwankungen des vierdimensionalen Raumes im Sinn der QGMD. Lineare Bewegungen werden dadurch nicht beeinflußt, da vom 4-D aus die Kräfte auch von innen auf die 3-D-Objekte wirken.

Beschleunigungen jedoch führen zu einer Änderung der mittleren Impulsrate der Quantenschwankungen des Raumes, worauf die Trägheit zurückzuführen ist. Der gleiche Effekt wirkt in diesem Fall. Vom 3-D-Raum aus steht die vierte Raumdimension senkrecht auf allen drei Dimensionen. Wenn sich der Kreisel dreht, führt also jede Neigung der Drehachse zu einer Impulsänderung in Richtung des 4-D, weshalb der Kreisel stabil bleibt. Legt man im obigen Fall von Abb. 50 ein zusätzliches Gewicht auf die Drehachse, so wirkt es in Richtung -z mit einer Kraft des Rades in Richtung +z. Vom 4-D aus wirken nun auf jedes einzelne Atom des Rades vom 4-D aus die Quantenimpulse und drücken das Rad nach unten. Durch die Rotation selbst hat dies einen Effekt, als ob das Rad von oben in Kontakt mit einer Platte kommt, wie es Abb. 50 zeigt. Bei anderer Drehrichtung ist der Effekt eben umgekehrt. Nach meiner Einschätzung ist dies einer der überzeugendsten Beweise für die Existenz der Wirkungen von Quantenschwankungen des vierdimensionalen Raumes auf Objekte des 3-D.
23. TOPOLOGIE DES MAGNETISMUS.
Im oberen Abschnitt wurden das elektrische Feld mit der Topologie eines Henkels beschrieben. Die Form selbst wird dabei aus der Raumenergie gebildet. An den Rändern dieser henkelförmigen Wirbel werden weitere Raumenergieteilchen mitgerissen und bilden einen Wirbelschlauch, ähnlich einem Tornado, dessen Wirkung mit dem Abstand schnell abnimmt.

In Abb. 51 ist die Situation skizziert. Die torusförmigen Ladungsträger sind hier der Einfachheit halber mit '+' und '-' symbolisiert. Der Schlauch entspricht einem Henkel der Art von Abb. 49. Aus der Rotationsrichtung des vierdimensionalen Schlauches ergibt sich konsequenterweise die Rotationsrichtung der vierdimensionalen Wirbelbildung.
Im 3-D erscheint nur noch die Projektion dieser Wirbel mit dem Effekt der unter 'Magnetismus bekannt ist. Somit ist klar, daß es keine Monopole von Magneten geben kann, aber einzelne elektrische Ladungen.
Im Neutron heben sich die Rotationen um die Hauptachse des Torus auf, da der überlagerte Elektrontorus die Drehung in Gegenrichtung hat. Was sich nicht aufhebt, ist die Drehung um die Schlauchachse, welche das magnetische Moment des Neutrons beibehält. Ein Elektron hat keinen kondensierten Kern wie ein Proton und stellt einen reinen Wirbel aus Raumenergie dar, weshalb das magnetische Moment auch entsprechend stark ist .
24. DER 'TUNNELEFFEKT' UND DIE 'STARKE KERNKRAFT'.
In einem Atomkern werden die Teilchen durch die 'Starke Kernkraft' zusammengehalten, welcher ich im vorigen Abschnitt die topologische Form eines Torus gab. Im dreidimensionalen Raum kann man sich den Potentialtrichter als einen Vulkanschlund vorstellen. Solange sich ein Teilchen im inneren Schlund befindet, kann es dem Vulkan nicht 'den Buckel 'runter rutschen'. Doch wenn es auch nur wenig über dem Rand ist, entfernt es sich unaufhörlich vom Kegelrand. Normalerweise hat aber ein Teilchen nicht genug Energie um über die Barriere zu springen, denn sonst wäre es nicht mehr darin. Innerhalb des von mir vorgeschlagenen Modells befindet sich aber der 3-D-Raum in ständigem Schwingungszustand und da kann es geschehen, daß solch ein Raumschwingung (K) zu dem Zeitpunkt an einem Atom vorbeikommt, an dem ein Teilchen im Potentialtrichter sich gerade nach oben bewegt (Abb. 52a).

Die Raumschwingung erniedrigt bei der Ankunft eine Seite des Trichters (b). Wenn nun bei der Passage des Schlundes das Teilchen sich gerade auf dem Umkehrpunkt der Bewegung befindet, dann kann es von der Raumschwingung aufgenommen und nach außen getragen werden (c). In diesem Modell braucht sich das Teilchen keine 'Energie von der HEISENBERGschen Unschärferelation zu leihen', wie bisher der Effekt erklärt wird . Das klingt, als ob die Wortbildung der Forscher eine reale Institution wäre, wie das Elektrizitätswerk oder eine Bank.
25. DIE 'WECHSELWIRKUNG DES NEUTRALEN STROMES’.
Wenn ein Elektron auf Materie trifft, ändert es zwar seine Energie und den Impuls, bleibt aber ein Elektron. Von Neutrinos, die elektrisch neutral sind, kennt man den Effekt, daß sie sich beim Zusammenstoß in ein geladenes Teilchen (Lepton) verwandeln. Doch man fand auch Reaktionen, bei denen dies nicht stattfand. Man benannte den Effekt: Wechselwirkung des neutralen Stromes.
Mit Hilfe der Topologie des Torus läßt sich dieser Effekt erklären. Ein Neutrino hat nur eine Rotation um die Schlauchachse des Torus und keine um die Zentralachse, weshalb es keine Ladung trägt.

Wenn es nun auf einen 4-D-Torus eines Masseteilchens stößt, dann bekommt der Torus des Neutrinos einen Drehimpuls um die Zentralachse, was sich nach außen als Ladung zeigt. In Ab. 96 entspricht dies der Bahn 2. Trifft das Neutrino jedoch im rechten Winkel auf den Teilchentorus, dann bekommt der Drehimpuls der Schlauchachse keine Überlagerung und die neutrale Ladung bleibt erhalten. Da sich das Ganze in quantisierten Systemen abspielt, gibt es vom rechten Winkel aus eine gewisse zulässige Breite der Abweichung, innerhalb der noch kein Ladungsimpuls erzeugt wird.
(Nun, als nächstes muss ich eine Selektion treffen und sie
auf Englisch übersetzen. Die Arbeit hier ist zu lang und zu
ausführlich für eine Veröffentlichung in einer Fachzeitschrift.
Ich werde auch nicht alles Wissen auf einmal herzeigen.
Ich lies hier auch die Zitierreferenzen weg.
Morgen werde ich noch eine kurze Abhandlung zu den
gravierenden Fehlern in Einsteins Theorie zur Relativität hochladen.
Ihr braucht davor nicht zurück zu schrecken!
Die Fehler sind so offensichtlich und gravierend, dass das
Wissen eines normalen Schulabschlusses ausreicht um die Sache
zu verstehen!)
-
nicole6

- ModeratorIn

- Beiträge: 2333
- Registriert: 11.09.2009, 13:01
- Wohnort: München
- Ich bin: ehemalige SexarbeiterIn
RE: Diskussionspapier: Modell für Zeit und Raum
Hier kommt nun die versprochene Kritik an Einsteins Theorie
der Relativität. Ich möchte noch voraus schicken, dass die
meisten Leute nicht wissen, dass Einstein seinen Nobelpreis
dafür erhielt, dass er theoretisch nachwies, dass Licht sowohl
Welleneigenschaften hat, wie auch Partikel sein kann.
Seine Relativitätstheorie hat ihm das Nobelpreiskomitee
"vergeben". Sie meinten damals, auch bekannte Physiker
machen Fehler!
Die folgende Arbeit ist ein Vortrag, den ich bei einer Physik-
Konferenz (8.11.-10.11.2002) an der Uni Tübingen vor
KollegInnen hielt.
Das heisst aber nicht, dass der Inhalt für Laien nicht zu
verstehen ist, im Gegenteil! Interesse vorausgesetzt,
kann jede(r) die einen Schulabschluss hat, den Gedankengang
nachvollziehen!
Noch eine Bemerkung: Eine "Theorie" besteht aus unterschiedlichen Teilen:
1) ein Modell, 2) eine mathematische Form, 3) einen Text,
der Modell und Formel verknüpft.
"Interne Gültigkeit" hat eine Theorie, wenn sie mit ihren
Ergebnissen und Voraussagen nicht den Voraussetzungen
widerspricht.
"Externe Gültigkeit" hat sie, wenn die Voraussagen für die
materielle Welt Übereinstimmung findet.
Was ich hier zeige ist, dass die Relation zwischen Modell und
Formel ungültig ist, sowohl für die interne, als auch externe
Gültigkeit. Dass die mathematischen Formeln manchmal
Ergebnisse bringen, heisst noch nicht, dass die Theorie stimmt!
######################################
21. EINSTEINS ZAUBERTRICKS.
1. Zaubertrick: das Kaninchen aus dem Hut.
In seinem Buch Über die spezielle und allgemeine Relativitätstheorie (1988,.(1917) Vieweg,
Braunschweig) , schreibt ALBERT EINSTEIN, daß die Wirkung der Beschleunigung durch die
Gravitation "weder vom Material noch vom physikalischen Zustande des Körpers im
geringsten abhängt".( Seite 42).
Dann aber bringt er ein Beispiel, bei dem ein Mann in einem Eisenbahnwagon sitzt, der
gleichförmig fährt. Wenn nun der Zug bremst, dann spürt der Mann eine Beschleunigung
nach vorne. Nun behauptet EINSTEIN, daß der Mann sein Erlebnis auch so deuten könne:
"Mein Bezugskörper (der Wagen) bleibt dauernd in Ruhe. Es herrscht aber (während der
Bremsungsperiode) in bezug auf denselben ein nach vorn gerichtetes, zeitlich veränderliches
Schwerefeld. Unter dem Einfluß des letzteren bewegt sich der Bahndamm samt der Erde
ungleichförmig derart, daß dessen ursprüngliche, nach rückwärts gerichtete Geschwindigkeit
immer mehr abnimmt. Dies Schwerefeld ist es auch, welches den Ruck des Beobachters
bewirkt" (Seite 46).
In Abb. 47 ist EINSTEINs Szenerie illustriert. In (a) schaut der Mann zum Fenster hinaus
und stellt sich vor, daß der Zug steht, aber die Landschaft und der Bahndamm ziehen
an ihm vorbei. Die relative Geschwindigkeit ist mit einem Pfeil symbolisiert. Wenn der
Zug nun bremst (negative Beschleunigung w), sieht der Mann nicht nur eine
Verlangsamung der relativen Geschwindigkeit der Objekte vor dem Fenster (b, unten),
sondern spürt zusätzlich dazu noch eine Beschleunigung m in Bezug zum Zugabteil
an seinem Leib.
Was wäre geschehen, wenn wirklich, wie EINSTEIN behauptet, auf den Zug "ein nach
vorne gerichtetes, zeitlich veränderliches Schwerefeld" gewirkt hätte? In der Abbildung
oben ist rechts eine Masse mit dem zeitlich veränderlichen Schwerefeld G eingetragen.
Nun, da gibt uns EINSTEIN selbst genau zwei Seiten zuvor die Antwort: Die Gravitation
wirkt auf alle Körper in gleicher Weise! Wenn also der Zug und der Bahndamm in ein
veränderliches Schwerefeld kommen, dann natürlich auch der Fahrgast darin, da die
Gravitation durch alle Objekte hindurch wirkt. Da die Gravitation für alle Massen
unabhängig vom Gewicht die gleiche Beschleunigung hervorruft, kann es unter keinen
Umständen im relativen Bezug zwischen Fahrgast, Zugabteil, Bahndamm und
Landschaft irgend einen Unterschied in der Beschleunigung geben. Ein typisches
Beispiel dafür ist das Eintreten einer Raumfähre in das Schwerefeld der Erde.
AstronautInnen und Raumfähre passieren ein zeitlich veränderliches Schwerefeld. In
der Kabine herrscht dann absolute Schwerelosigkeit. Wenn allerdings die
Bremsraketen zünden, dann spüren die Personen in der Fähre eine Beschleunigung.
Aber die hat eindeutig keinen Ursprung in der Gravitation. EINSTEINs geht hier unter die
Wortmagier und Zauberkünstler, die mit ihren Tricks das Publikum einwickeln können
und Kaninchen aus dem Hut herauszaubern.
2. Zaubertrick: die Taube aus der Hosentasche.
Ein Mann schwebe in einem geräumigen Kasten in der Größe eines Zimmers im
schwerelosen Bereich des Weltraums. Nun würde jemand von außen den Kasten an
einem Seil beschleunigen, welches an der Decke befestigt ist. Der Mann im Zimmer
spürt jetzt eine Kraft nach unten. Laut EINSTEIN könne er nicht feststellen, um welche
Art von Kraft es sich handeln soll, selbst wenn er die Naturgesetze kenne und mit ihrer
Messung vertraut sei.
Tauschen wir den Mann durch eine Wissenschaftlerin aus und lassen sie einmal
messen. Das Zimmer ist vier Meter hoch. Nun mißt sie mit einer empfindlichen
Federwaage die Beschleunigungskräfte im Abstand von einem Meter und hat damit
fünf Meßpunkte, welche sie auf ein Papier überträgt. Dabei sind drei Möglichkeiten
gegeben:
1.) Alle Werte sind gleich: es handelt sich um eine lineare Beschleunigung des
Kastens in Richtung zur Decke. (F = konstant)
2.) die Werte nehmen linear ab: Der Kasten rotiert um ein Zentrum, welches in der
Verlängerung zur Decke liegt. (F ~ 1/R)
3.) die Werte nehmen in nicht-linearer Weise ab: Der Kasten steht in einem Schwerefeld. (F ~ 1/R²)
Die Wissenschaftlerin kann also auf Grund der Proportionalitäten eindeutig bestimmen, welche Art von Kraft auf sie und das Zimmer wirkt.
3. Zaubertrick: Der Elefant aus der Kaffeetasse.
EINSTEIN geht von einem Gebiet aus, in dem Schwerelosigkeit herrscht. In Bezug zu
einem Punkt der die Koordinaten festlegt, soll sich eine drehende Scheibe befinden,
auf der ein Beobachter sitzt. Den Beobachter schätzt EINSTEIN als so dumm ein,
daß er nicht merkt, daß er auf einer drehenden Scheibe sitzt, sondern dieser solle
glauben, EINSTEINs Relativitätstheorie sei richtig und die Zentripedalkraft die er spürt,
solle von einem zugegebenermaßen etwas 'seltsamen' Schwerefeld kommen.
Zwei gleiche Uhren werden nun von dem Mann so auf der Scheibe verteilt, daß sich
die eine im Mittelpunkt M, die andere am Rand R der Scheibe befinde (nächste Abbildung).
Nun behauptet EINSTEIN, daß die Uhr am Rand R im Bezug zum Koordinatensystem
langsamer gehe, als die in der Mitte M. Er bezieht sich dabei auf §12. Schaut man dort
nach, so beschreibt er dort keine Beschleunigungen (die Uhr am Rand ist einer
Kreisbeschleunigung unterworfen), sondern lineare Bewegungen. Außerdem benutzt
er als Formel die Lorenztransformationen, die
1.) nur für lineare Transformationen verwendbar sind, denn es wird y'=y und z'=z gesetzt, und die
2.) für die x-Koordinate eine Geschwindigkeit im Zähler haben, d.h. einen Vektor und nicht den Betrag der Geschwindigkeit !
Für die x-Richtung ist die LORENTZ-Transformation: x' = (x-vt)(1-v²/c²)-1/2..
EINSTEIN läßt aber den Vektorstatus von v verschwinden und schreibt einfach v.
Solange man nur parallele Geschwindigkeiten in eine Richtung betrachtet, ist dies ok,
nicht aber wenn Beschleunigungen und Richtungsänderungen erfolgen!
Die Vertuschung des Vektorstatus der Geschwindigkeit v ist der eigentliche Zaubertrick
EINSTEINs, denn nur so kann er seine Wortmagie weiterführen. Wenn aber das
Zeitverhalten von Uhren von der linearen Geschwindigkeit der Uhr abhängt,
dann sind in seinem Beispiel die Geschwindigkeitsvektoren A und A', bzw. B und B'
entgegengesetzt, heben sich als Vektoren auf und werden Null. Dies gilt für jeden
Punkt der drehenden Scheibe! Fazit: beide Uhren gehen genau gleich.
Doch die Wortmagie hört hier noch nicht auf. Der Mann soll nun den Umfang und den
Durchmesser der Scheibe messen und laut EINSTEIN würde er, wegen der postulierten
Verkürzung des Randes, bei der Division der Meßergebnisse eine größere Zahl als Pi
finden. Dies setzt aber selbst innerhalb EINSTEINs Theorie voraus, daß sich der
Maßstab nicht mitdreht und sich nicht auf der Scheibe befindet. Andernfalls würde er
nämlich die gleiche Verkürzung erfahren wie der Rand, und bei der Division käme doch
die Zahl Pi heraus.
Mit diesen Worttricks versucht EINSTEIN dann im Anhang (Seite 87-91) die
Rotverschiebung mit abenteuerlichen Argumentationssprüngen zu begründen:
Von den linearen Formeln der LORENTZ-Transformationen schließt er auf rotierende
Systeme. Die darin wirkende Zentripedalkraft setzt er dann mit den Wirkungen der
Gravitation gleich, auch wenn die Formeln völlig unterschiedliche Proportionalitäten
zeigen (F1 ~ 1/R und F2 ~ 1/R²). Von dort aus nimmt er seinen Uhrentrick und setzt die
Uhr mit einem Spektrallinien emittierenden Atom gleich. Als Schlußfolgerung zieht er
nun die Behauptung, die Frequenz emittierter Photonen sei vom Potential des
Gravitationsfeldes abhängig. EINSTEIN weiß, daß sein Wortzauber mit der Definition
von 'Gleichzeitigkeit' zusammenhängt, wie er es in der speziellen Relativitätstheorie
gemacht hat.
Doch hier würde diese Überlegung versagen, weshalb er mit folgenden
Worten ablenkt: "Eine vernünftige Definition der Zeit mit Hilfe von relativ zum
Bezugskörper ruhend angeordneten Uhren ist also nicht möglich. Eine ähnliche
Schwierigkeit zeigt sich, wenn man versucht, unsere frühere Definition der
Gleichzeitigkeit hier anzuwenden, worauf ich nicht weiter eingehen will.".
(EINSTEIN, ALBERT; 1988; Uber die spezielle und die allgemeine Relativitätstheorie;
Vieweg, Braunschweig, , (Nachdruck von 1917); Seite 53.)
Offensichtlich kann er nicht darauf eingehen, denn sonst käme der Trick an die
Öffentlichkeit. Solche Wortmagie wird oft von Wissenschaftlern verwendet,
wenn sie glauben eine gute Idee zu haben, aber keine rationalen Argumente dafür
angeben können. PAUL FEYERABEND nennt ein Beispiel mit GALILEI: "Galilei behält
wegen seines Stils und seiner geschickten Überredungsmethoden die Oberhand,
weil er auch in italienisch und nicht nur in lateinisch schreibt und weil er sich an Leute
wendet, die gefühlsmäßig gegen die alten Ideen und die mit ihnen verbundenen
Maßstäbe der Gelehrsamkeit eingenommen sind
(FEYERABEND, PAUL; 1991; Wider den Methodenzwang; Suhrkamp, Frankfurt, Seite 184.)
Doch es war EINSTEIN schon damals klar, daß die Konsequenzen aus seinen
Konstruktionen zu Widersprüchen führen: "Es ergibt sich aber eine merkwürdige
Schwierigkeit. Die (theoretisch kaum bezweifelbare) Interpretation der von HUBBLE
gefundenen galaktischen Linienverschiebungen als Expansion führt auf einen Anfang
der Expansion, die 'nur' etwa 109 Jahre zurückliegt, während die physikalische
Astronomie es wahrscheinlich erscheinen läßt, daß die Entwicklung der einzelnen
Sterne und Sternsysteme erheblich größere Zeiten erforderte."
(EINSTEIN, ALBERT; 1988; Uber die spezielle und die allgemeine Relativitätstheorie;
Vieweg, Braunschweig, , (Nachdruck von 1917); Seite 91.)
Diese Schwierigkeiten haben bis heute nicht aufgehört, wie die Veröffentlichungen zeigen:
Eine ausführliche Beschreibung der Probleme findet man bei:
TREFIL, JAMES; 1993; Fünf Gründe, warum es die Welt nicht geben kann. Die Astrophysik der dunklen Materie; Rowohlt, Hamburg;
Weitere Informationen:
KAYSER, RAINER; 1996; Tempolimit im All. Galaxien im Gleichschritt erschüttern das Weltbild der Kosmologen; ZEIT, 12/1996;
KLEIN, STEFAN; 1995; Schildbürgertraum. Einstein sagte ihre Existenz voraus, doch bislang sind weder Gravitationswellen noch schwarze Löcher im All wirklich nachgewiesen; ZEIT, 4/1995
SCHNABEL, ULRICH;1992; Wenn Astronomen Rot sehen. "Hubble Bubbles" und gestückelte
Geschwindigkeiten im Universum bereiten den Forschern Kopfzerbrechen; ZEIT, 46/1992
1992; Krach um den Urknall.Seit zwanzig Jahren streiten die Kosmologen über die Expansion des Weltraums. Ist das Universum etwa jünger als seine Sterne ?; ZEIT, 36/1992;
1993; Krach um den Urknall; ZEIT, 24/1993;
1994; Urknall auf der Bühne; ZEIT, 45/1994;
1994; Unbeirrbarer Urknallrebell. Seit über vierzig Jahren denkt Sir Fred Hoyle gegen das
Wissenschaftliche Establishment an; ZEIT, 1/1995;
1996; Das große Gehubble um den Urknall; ZEIT, 51/1995;
TAMMAN, ANDREAS; 1995; Streit um Jahrmilliarden; GEO, 1/1995, (S.172-176);
der Relativität. Ich möchte noch voraus schicken, dass die
meisten Leute nicht wissen, dass Einstein seinen Nobelpreis
dafür erhielt, dass er theoretisch nachwies, dass Licht sowohl
Welleneigenschaften hat, wie auch Partikel sein kann.
Seine Relativitätstheorie hat ihm das Nobelpreiskomitee
"vergeben". Sie meinten damals, auch bekannte Physiker
machen Fehler!
Die folgende Arbeit ist ein Vortrag, den ich bei einer Physik-
Konferenz (8.11.-10.11.2002) an der Uni Tübingen vor
KollegInnen hielt.
Das heisst aber nicht, dass der Inhalt für Laien nicht zu
verstehen ist, im Gegenteil! Interesse vorausgesetzt,
kann jede(r) die einen Schulabschluss hat, den Gedankengang
nachvollziehen!
Noch eine Bemerkung: Eine "Theorie" besteht aus unterschiedlichen Teilen:
1) ein Modell, 2) eine mathematische Form, 3) einen Text,
der Modell und Formel verknüpft.
"Interne Gültigkeit" hat eine Theorie, wenn sie mit ihren
Ergebnissen und Voraussagen nicht den Voraussetzungen
widerspricht.
"Externe Gültigkeit" hat sie, wenn die Voraussagen für die
materielle Welt Übereinstimmung findet.
Was ich hier zeige ist, dass die Relation zwischen Modell und
Formel ungültig ist, sowohl für die interne, als auch externe
Gültigkeit. Dass die mathematischen Formeln manchmal
Ergebnisse bringen, heisst noch nicht, dass die Theorie stimmt!
######################################
21. EINSTEINS ZAUBERTRICKS.
1. Zaubertrick: das Kaninchen aus dem Hut.
In seinem Buch Über die spezielle und allgemeine Relativitätstheorie (1988,.(1917) Vieweg,
Braunschweig) , schreibt ALBERT EINSTEIN, daß die Wirkung der Beschleunigung durch die
Gravitation "weder vom Material noch vom physikalischen Zustande des Körpers im
geringsten abhängt".( Seite 42).
Dann aber bringt er ein Beispiel, bei dem ein Mann in einem Eisenbahnwagon sitzt, der
gleichförmig fährt. Wenn nun der Zug bremst, dann spürt der Mann eine Beschleunigung
nach vorne. Nun behauptet EINSTEIN, daß der Mann sein Erlebnis auch so deuten könne:
"Mein Bezugskörper (der Wagen) bleibt dauernd in Ruhe. Es herrscht aber (während der
Bremsungsperiode) in bezug auf denselben ein nach vorn gerichtetes, zeitlich veränderliches
Schwerefeld. Unter dem Einfluß des letzteren bewegt sich der Bahndamm samt der Erde
ungleichförmig derart, daß dessen ursprüngliche, nach rückwärts gerichtete Geschwindigkeit
immer mehr abnimmt. Dies Schwerefeld ist es auch, welches den Ruck des Beobachters
bewirkt" (Seite 46).
In Abb. 47 ist EINSTEINs Szenerie illustriert. In (a) schaut der Mann zum Fenster hinaus
und stellt sich vor, daß der Zug steht, aber die Landschaft und der Bahndamm ziehen
an ihm vorbei. Die relative Geschwindigkeit ist mit einem Pfeil symbolisiert. Wenn der
Zug nun bremst (negative Beschleunigung w), sieht der Mann nicht nur eine
Verlangsamung der relativen Geschwindigkeit der Objekte vor dem Fenster (b, unten),
sondern spürt zusätzlich dazu noch eine Beschleunigung m in Bezug zum Zugabteil
an seinem Leib.

Was wäre geschehen, wenn wirklich, wie EINSTEIN behauptet, auf den Zug "ein nach
vorne gerichtetes, zeitlich veränderliches Schwerefeld" gewirkt hätte? In der Abbildung
oben ist rechts eine Masse mit dem zeitlich veränderlichen Schwerefeld G eingetragen.
Nun, da gibt uns EINSTEIN selbst genau zwei Seiten zuvor die Antwort: Die Gravitation
wirkt auf alle Körper in gleicher Weise! Wenn also der Zug und der Bahndamm in ein
veränderliches Schwerefeld kommen, dann natürlich auch der Fahrgast darin, da die
Gravitation durch alle Objekte hindurch wirkt. Da die Gravitation für alle Massen
unabhängig vom Gewicht die gleiche Beschleunigung hervorruft, kann es unter keinen
Umständen im relativen Bezug zwischen Fahrgast, Zugabteil, Bahndamm und
Landschaft irgend einen Unterschied in der Beschleunigung geben. Ein typisches
Beispiel dafür ist das Eintreten einer Raumfähre in das Schwerefeld der Erde.
AstronautInnen und Raumfähre passieren ein zeitlich veränderliches Schwerefeld. In
der Kabine herrscht dann absolute Schwerelosigkeit. Wenn allerdings die
Bremsraketen zünden, dann spüren die Personen in der Fähre eine Beschleunigung.
Aber die hat eindeutig keinen Ursprung in der Gravitation. EINSTEINs geht hier unter die
Wortmagier und Zauberkünstler, die mit ihren Tricks das Publikum einwickeln können
und Kaninchen aus dem Hut herauszaubern.
2. Zaubertrick: die Taube aus der Hosentasche.
Ein Mann schwebe in einem geräumigen Kasten in der Größe eines Zimmers im
schwerelosen Bereich des Weltraums. Nun würde jemand von außen den Kasten an
einem Seil beschleunigen, welches an der Decke befestigt ist. Der Mann im Zimmer
spürt jetzt eine Kraft nach unten. Laut EINSTEIN könne er nicht feststellen, um welche
Art von Kraft es sich handeln soll, selbst wenn er die Naturgesetze kenne und mit ihrer
Messung vertraut sei.
Tauschen wir den Mann durch eine Wissenschaftlerin aus und lassen sie einmal
messen. Das Zimmer ist vier Meter hoch. Nun mißt sie mit einer empfindlichen
Federwaage die Beschleunigungskräfte im Abstand von einem Meter und hat damit
fünf Meßpunkte, welche sie auf ein Papier überträgt. Dabei sind drei Möglichkeiten
gegeben:
1.) Alle Werte sind gleich: es handelt sich um eine lineare Beschleunigung des
Kastens in Richtung zur Decke. (F = konstant)
2.) die Werte nehmen linear ab: Der Kasten rotiert um ein Zentrum, welches in der
Verlängerung zur Decke liegt. (F ~ 1/R)
3.) die Werte nehmen in nicht-linearer Weise ab: Der Kasten steht in einem Schwerefeld. (F ~ 1/R²)
Die Wissenschaftlerin kann also auf Grund der Proportionalitäten eindeutig bestimmen, welche Art von Kraft auf sie und das Zimmer wirkt.
3. Zaubertrick: Der Elefant aus der Kaffeetasse.
EINSTEIN geht von einem Gebiet aus, in dem Schwerelosigkeit herrscht. In Bezug zu
einem Punkt der die Koordinaten festlegt, soll sich eine drehende Scheibe befinden,
auf der ein Beobachter sitzt. Den Beobachter schätzt EINSTEIN als so dumm ein,
daß er nicht merkt, daß er auf einer drehenden Scheibe sitzt, sondern dieser solle
glauben, EINSTEINs Relativitätstheorie sei richtig und die Zentripedalkraft die er spürt,
solle von einem zugegebenermaßen etwas 'seltsamen' Schwerefeld kommen.
Zwei gleiche Uhren werden nun von dem Mann so auf der Scheibe verteilt, daß sich
die eine im Mittelpunkt M, die andere am Rand R der Scheibe befinde (nächste Abbildung).
Nun behauptet EINSTEIN, daß die Uhr am Rand R im Bezug zum Koordinatensystem
langsamer gehe, als die in der Mitte M. Er bezieht sich dabei auf §12. Schaut man dort
nach, so beschreibt er dort keine Beschleunigungen (die Uhr am Rand ist einer
Kreisbeschleunigung unterworfen), sondern lineare Bewegungen. Außerdem benutzt
er als Formel die Lorenztransformationen, die
1.) nur für lineare Transformationen verwendbar sind, denn es wird y'=y und z'=z gesetzt, und die
2.) für die x-Koordinate eine Geschwindigkeit im Zähler haben, d.h. einen Vektor und nicht den Betrag der Geschwindigkeit !
Für die x-Richtung ist die LORENTZ-Transformation: x' = (x-vt)(1-v²/c²)-1/2..
EINSTEIN läßt aber den Vektorstatus von v verschwinden und schreibt einfach v.
Solange man nur parallele Geschwindigkeiten in eine Richtung betrachtet, ist dies ok,
nicht aber wenn Beschleunigungen und Richtungsänderungen erfolgen!

Die Vertuschung des Vektorstatus der Geschwindigkeit v ist der eigentliche Zaubertrick
EINSTEINs, denn nur so kann er seine Wortmagie weiterführen. Wenn aber das
Zeitverhalten von Uhren von der linearen Geschwindigkeit der Uhr abhängt,
dann sind in seinem Beispiel die Geschwindigkeitsvektoren A und A', bzw. B und B'
entgegengesetzt, heben sich als Vektoren auf und werden Null. Dies gilt für jeden
Punkt der drehenden Scheibe! Fazit: beide Uhren gehen genau gleich.
Doch die Wortmagie hört hier noch nicht auf. Der Mann soll nun den Umfang und den
Durchmesser der Scheibe messen und laut EINSTEIN würde er, wegen der postulierten
Verkürzung des Randes, bei der Division der Meßergebnisse eine größere Zahl als Pi
finden. Dies setzt aber selbst innerhalb EINSTEINs Theorie voraus, daß sich der
Maßstab nicht mitdreht und sich nicht auf der Scheibe befindet. Andernfalls würde er
nämlich die gleiche Verkürzung erfahren wie der Rand, und bei der Division käme doch
die Zahl Pi heraus.
Mit diesen Worttricks versucht EINSTEIN dann im Anhang (Seite 87-91) die
Rotverschiebung mit abenteuerlichen Argumentationssprüngen zu begründen:
Von den linearen Formeln der LORENTZ-Transformationen schließt er auf rotierende
Systeme. Die darin wirkende Zentripedalkraft setzt er dann mit den Wirkungen der
Gravitation gleich, auch wenn die Formeln völlig unterschiedliche Proportionalitäten
zeigen (F1 ~ 1/R und F2 ~ 1/R²). Von dort aus nimmt er seinen Uhrentrick und setzt die
Uhr mit einem Spektrallinien emittierenden Atom gleich. Als Schlußfolgerung zieht er
nun die Behauptung, die Frequenz emittierter Photonen sei vom Potential des
Gravitationsfeldes abhängig. EINSTEIN weiß, daß sein Wortzauber mit der Definition
von 'Gleichzeitigkeit' zusammenhängt, wie er es in der speziellen Relativitätstheorie
gemacht hat.
Doch hier würde diese Überlegung versagen, weshalb er mit folgenden
Worten ablenkt: "Eine vernünftige Definition der Zeit mit Hilfe von relativ zum
Bezugskörper ruhend angeordneten Uhren ist also nicht möglich. Eine ähnliche
Schwierigkeit zeigt sich, wenn man versucht, unsere frühere Definition der
Gleichzeitigkeit hier anzuwenden, worauf ich nicht weiter eingehen will.".
(EINSTEIN, ALBERT; 1988; Uber die spezielle und die allgemeine Relativitätstheorie;
Vieweg, Braunschweig, , (Nachdruck von 1917); Seite 53.)
Offensichtlich kann er nicht darauf eingehen, denn sonst käme der Trick an die
Öffentlichkeit. Solche Wortmagie wird oft von Wissenschaftlern verwendet,
wenn sie glauben eine gute Idee zu haben, aber keine rationalen Argumente dafür
angeben können. PAUL FEYERABEND nennt ein Beispiel mit GALILEI: "Galilei behält
wegen seines Stils und seiner geschickten Überredungsmethoden die Oberhand,
weil er auch in italienisch und nicht nur in lateinisch schreibt und weil er sich an Leute
wendet, die gefühlsmäßig gegen die alten Ideen und die mit ihnen verbundenen
Maßstäbe der Gelehrsamkeit eingenommen sind
(FEYERABEND, PAUL; 1991; Wider den Methodenzwang; Suhrkamp, Frankfurt, Seite 184.)
Doch es war EINSTEIN schon damals klar, daß die Konsequenzen aus seinen
Konstruktionen zu Widersprüchen führen: "Es ergibt sich aber eine merkwürdige
Schwierigkeit. Die (theoretisch kaum bezweifelbare) Interpretation der von HUBBLE
gefundenen galaktischen Linienverschiebungen als Expansion führt auf einen Anfang
der Expansion, die 'nur' etwa 109 Jahre zurückliegt, während die physikalische
Astronomie es wahrscheinlich erscheinen läßt, daß die Entwicklung der einzelnen
Sterne und Sternsysteme erheblich größere Zeiten erforderte."
(EINSTEIN, ALBERT; 1988; Uber die spezielle und die allgemeine Relativitätstheorie;
Vieweg, Braunschweig, , (Nachdruck von 1917); Seite 91.)
Diese Schwierigkeiten haben bis heute nicht aufgehört, wie die Veröffentlichungen zeigen:
Eine ausführliche Beschreibung der Probleme findet man bei:
TREFIL, JAMES; 1993; Fünf Gründe, warum es die Welt nicht geben kann. Die Astrophysik der dunklen Materie; Rowohlt, Hamburg;
Weitere Informationen:
KAYSER, RAINER; 1996; Tempolimit im All. Galaxien im Gleichschritt erschüttern das Weltbild der Kosmologen; ZEIT, 12/1996;
KLEIN, STEFAN; 1995; Schildbürgertraum. Einstein sagte ihre Existenz voraus, doch bislang sind weder Gravitationswellen noch schwarze Löcher im All wirklich nachgewiesen; ZEIT, 4/1995
SCHNABEL, ULRICH;1992; Wenn Astronomen Rot sehen. "Hubble Bubbles" und gestückelte
Geschwindigkeiten im Universum bereiten den Forschern Kopfzerbrechen; ZEIT, 46/1992
1992; Krach um den Urknall.Seit zwanzig Jahren streiten die Kosmologen über die Expansion des Weltraums. Ist das Universum etwa jünger als seine Sterne ?; ZEIT, 36/1992;
1993; Krach um den Urknall; ZEIT, 24/1993;
1994; Urknall auf der Bühne; ZEIT, 45/1994;
1994; Unbeirrbarer Urknallrebell. Seit über vierzig Jahren denkt Sir Fred Hoyle gegen das
Wissenschaftliche Establishment an; ZEIT, 1/1995;
1996; Das große Gehubble um den Urknall; ZEIT, 51/1995;
TAMMAN, ANDREAS; 1995; Streit um Jahrmilliarden; GEO, 1/1995, (S.172-176);
-
nicole6

- ModeratorIn

- Beiträge: 2333
- Registriert: 11.09.2009, 13:01
- Wohnort: München
- Ich bin: ehemalige SexarbeiterIn
RE: Diskussionspapier: Modell für Zeit und Raum
so, jetzt ist es soweit. Da es hier kalt ist und Dauerregen hat,
entschloss ich mich endlich, meine Theorie von oben der
weltweit wichtigsten Fachzeitschrift für Physik anzubieten,
nämlich Physical Review Letters. Die Artikel sind im Umfang limitiert.
So habe ich nun zu Beginn nur die wichtigsten Inhalte ins
englische übersetzt und hingeschickt.
Zur Absicherung, dass mir niemand diese Ideen klauen kann,
und als eigene veröffentlichen, lade ich hier die englisch Fassung hoch.
Nicole
entschloss ich mich endlich, meine Theorie von oben der
weltweit wichtigsten Fachzeitschrift für Physik anzubieten,
nämlich Physical Review Letters. Die Artikel sind im Umfang limitiert.
So habe ich nun zu Beginn nur die wichtigsten Inhalte ins
englische übersetzt und hingeschickt.
Zur Absicherung, dass mir niemand diese Ideen klauen kann,
und als eigene veröffentlichen, lade ich hier die englisch Fassung hoch.
Nicole
-
nicole6

- ModeratorIn

- Beiträge: 2333
- Registriert: 11.09.2009, 13:01
- Wohnort: München
- Ich bin: ehemalige SexarbeiterIn
RE: Diskussionspapier: Modell für Zeit und Raum
Conclusions from a model for a real 5-D-Space
Abstract: the fact, that we have no direct experiences with more than three space dimensions should not stop us from studying the possibility of a real existence. For many other objects in science their existence was proofed only indirectly by deduction, or by the effects. This indirect proof is also possible for a real 5-D space. With this hypothesis a lot of problems find a logic explanation. But the most pleasant effect is, it leads to a geometrical model for charge and magnetism that enhances a general understanding of electric forces and the inner structure of particles. In addition, it allows a deduction of the gravitational formula.
Key words: gravitation, quarks, mass formation.
About parity transformation
To imagine space with more than three dimensions is nothing new. Here we draw the conclusions, if space contains real five dimension. Just to go one step further to four real space dimensions would not be valid mathematically, because any space that allows parity transformation must be surrounded by two dimensions higher as the space where the transformation occurs. Nearly two hundred years ago the mathematician Möbius produced for this statement the general proof .
A Necker-cube is am object that produces visually a parity transformation experience in 3-D space. If one looks for a while to the cube skeleton on the left of figure 1(a), it will change in a certain rhythm its appearance. For a while one sees the view like in (b), then for another while like in (c). But these two versions, (b) and (c) are different cubes, like the right and left gloves for hands! If we take for instance the corner E: in (b): the corner A is before E, but in (c) it is in the back! Here a parity conversion occurs in front of our eyes! As it is the same cube when we look at it, the parity transformation turns the inside of the cube outside! In three dimensional space this is not possible, but we can still observe it! That means, we have to ad at least two more dimensions to be in line with he Möbius theorem.
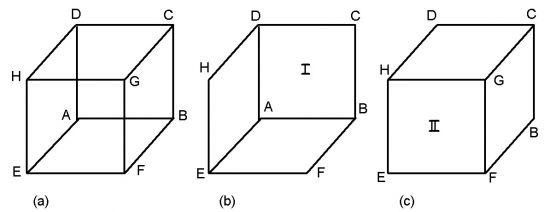
figure 01: the Necker-cube.
A definition of "time"
What kind of laws would be observable if space would have real 5 dimensions?
Before one can study these laws, one has to find a solid definition for the term "time". To start with it, a theorem of Poincaré is used. It proves, that nature changes in quantum steps . With this, the definition of quantum-time is:
"time" is the gap between the appearance of an object, and the exchange by another.
This definition works for all kind of time models, even for human sciences, like psychology and sociology!
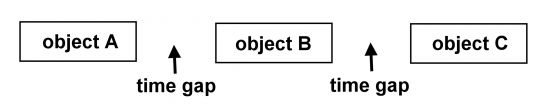
figure 02: "time" definition.
With this definition of time, combined with the Einstein-Minkowsky formula, one can create a formula for space with any number of dimensions:
t(sec) x c(m/sec) x i = s(m),
with "t" as the quantum time in seconds, "c" as the constant for light in m/sec, and "i" as the imaginary unit that turns the time vector 90 degrees.
This leads to a model of quantum space.
Now it is possible to create a model for a 4-D space, embedded in a 5-D space. In figure 03 the x and y dimensions of a 3-D space got compressed into one. The point A stands still until it starts moving at time (0), and stops at time point (4). Projected over the time scale, the point describes a kind of s-shape with infinite ends. But one can see it also in a different way: the s-shape is a given object extended in 4-D, and the 3-D-frame moves through 4D. For observers inside the 3-D the results would be the same.
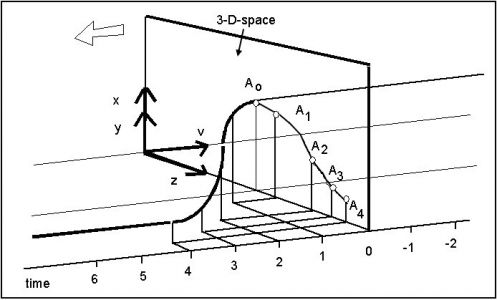
figure03: time and 4-D space
Co-dimension
Normally one needs for the mathematical representation as many equations as there are dimensions. For a space with one hundred dimensions one needs as many equations. But if one observes an object in space, the number on equations is reduced to the difference between the object dimension and the embedding space. So, an object with 99 dimensions in a embedding space of 100 dimensions needs only one equation! Here the term co-dimension is in use. Objects with the same co-dimension have the same features. A 2-D plane divides a 3-D space in two parts, and in an object with the c-dimension 1. Working with co-dimensions becomes interesting, if one does not know exactly how many elements take part, and where the number of elements even can change. Then one talks about fuzzy elements. In general, the basic features of a co-dimension remain, even if one takes off the "superfluous" elements.
An example: a cut of a sphere with a 2-D space creates the co-dimension 3-2=1.
That means, the cut area "C" can be described by one equation, even if it is a multi-dimensional object; C=2r*.
If one considers the existence of higher spaces, then the conclusion is, that the 3-D space-matrix, as we perceive it, can vibrate into the 4-D, like a shaken tapestry into 3-D-sapce. That would add to the longitudinal and transversal waves a third kind of wave pattern, that we can call "matrix-wave". This matrix wave will have effects also inside 3-D objects, because from the 4-D, the inside of 3-D is as open as the inside of a circle can be seen from 3-D ! As an ad-hoc hypothesis one can assume, that the waves of the 4-D-spaces matrix moves with he the so called "sped of light". Later in this paper more proof will be presented to make this hypothesis more probable.
Deduction of the gravitational formula.
In the 5th letter to Newton (Clarke), Leibnitz wrote about the explanation of gravitation by impulse forces . This is not possible with pure 3-D objects in a 3-D only space. But if the objects takes part inside a 4-D space, then the explanation is as easy as follows:
To understand the procedure it is important to remind oneself, that forces from the 4-D-space have effects also on the inside of solid 3-D-objects! Withou this fact, the procedure is not valid, because this represents the fundamental difference to forces in 3-D-space on 3-D objects!
Supposed, the 4-D space is agitated like the waves in a harbor, coming criss-cross from all sides. A single floating object in the water would just remain where it is. It would vibrate, but the average of the impulses coming from the waves would be zeroed out.
The situation changes with a second object in this condition: each object will now block the wave impulses along a line between each other. With time they will come close together! This is the basic idea behind the following deduction for two 3-D objects, T1 and T2 , embedded in a 4-D-space.
Now, the resulting force Fres , through the mutual shielding of T1 and T2 , is caused by the average force Fm of the impulses from the 4-D. Fm can be represented by the density of the impulse field. If the energy density of Fm is rising, under the condition that the rest remains as it is, then the proportion with Fres is lowering. In short: Fm ~ 1/Fres.
Fres ~ 1/Fm. (1)
F1 is the force on the object T1 , and F2 is the force on the object T2 . Then, obviously Fres is proportional with F1 and F2 , because Fres rises if F1 or F2 rises. In short:
Fres ~ F1 and Fres ~ F2 (2)
Taken together, with the proportional constant k we get:
Fres = k F1F2 /Fm (3)
In general terms, one must start with the condition, that both objects are in a moving state. Then one of it can be considered as a relative reference stand still point, and the second as moving relative to the first one.
With m1 for the mass of T1 , m2 for the mass of T2 , and R for the distance of m1 and m2, one needs to insert for the active forces the centripetal laws. Together, with v as the average speed of the quantum impulses from the above mentioned matrix wave field, one gets
F1 = m1v²/R und F2 = m2v²/R (4)
Now we put (4) into (3) and get
Fres. = km1m2v4/FmR² (5).
Next, we unite all constants into one unit K, and kv4/Fm becomes K.
The values of K are: : [m4s2/s4m kg] = [m3/s2kg]
And the formula (5) becomes
Fres. = Km1m2/R² [m3/s2kg] (6)
This equation (6) has exactly the same features and units as the gravitational formula!
figure 04: 4-D gravitation model
anti-gravity
The considerations above imagined a field of impulses from a 4-D space with a certain average frequency. If one could find out this frequency and produce it artificially with a certain intensity, one could enhance the weakened field between the objects and produce anti-gravity.
inertia
This model allows also an explanation of inertia. As the inside of 3-D mass objects are accessible and open from 4-D, the average of the sum of impulses from 4_D are the same if the 3-D object moves steadily or stands still. Acceleration is change of speed, and this needs a new dimension: now the effects of the 4-D-impulses become sensible as we know it from the difference in air or water by through speed changes! The same difference is active for a 3-D-object embedded in 4-D, changing from linear speed to acceleration! The difference is only, that for a 3-D-object in 3-D space the air resistance depends on the surface, but for the acceleration of a 3-D object embedded in a 4-D space it depends on all particles of the object, also those that are found inside.
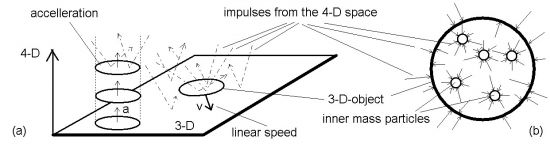
figure05: inertia model
The torus as a spin model for elementary particles
So far, science uses as a model for particles spheres. If our visible and touchable 3-D-objects would be part of a higher dimensional real existing space, then another model would also be possible: a 4-D-hyper-torus. A torus has a very particular feature, that sets it apart from all other objects: it can contain two independent rotary axes. A bicycle tube is a good example to understand the principles: The bike tube has a valve, that we will use as a reference point. Usually it is mounted in a way, that it points towards the bicycle hub. Now, the tube can turn around the hub H, then the valve points always inside. But the tube can also turn around its middle axis A! Then it turns from the inside out and back inside. These two ways of turns are totally independent!
That means, any kind of combination is possible. Let us start with the easiest: the tube moves in a way, that for a 360 degree turn around H the valve turns 180 degrees around A. Another 360 degree turn around H is needed, before the valve and all other particles of the bike tube are in the original position.
The proportion of the two turns A and H are then ½. Obviously, with this model all kind of proportions are possible! This feature of a torus makes it a perfect model for explaining spin for elementary particles!
Each of the two turning axes A and H of the torus can be in one of the three kind of states, two moving ones and one stand still. That makes up to a 9-fold pattern of 8 moving combinations, and one with zero movement.
figure 06: torus dynamic combination table
J. A. Wheeler showed also a connection between spin ½ and the torus. He explains it using a projection of a 4-D hyper-cube, where the corners of two cubes are connected by lines. Turning one of these cubes two times 360 degrees will twist the strings. If we turn now the twisted cube around the other, the strings will be free again! As a very simple experiment one can take a stiff belt and fix one end on the table. The four edges of the belts represent the four strings. Now the free end of the belt gets twisted two times 360 degrees. Then the twisted free end has to be turned around the fixed end, keeping the orientation. As a result the twist disappears! But this does not work if the belt gets twisted only one time 360 degrees!
The torus model and charge
For an easier understanding, the torus in the graphic shows at the center an opening. But for the following calculation a torus with no opening is considered!
During one turn the center of the torus covers the distance 2r*, that will be ad-hoc identified with the electric charge Q: 2r* = Q.
A torus with no hole inside has a surface of 2r*.
So, the whole surface that moves through the control area in one turn is
4*2r2 = Q².
Above is mentioned, that the propagation of the 4-D-wave pattern follows the speed of light c. In case, the turns of the torus are proportional with this pattern, then we have to divide the charge by c, getting Q²/c. For quantum objects we also have to divide this with the Heisenberg Constant h/2*, and we will get 2*Q²/ch. If we set for Q the charge of an electron, the result is the Fine-Structure-Constant Alpha!
An interesting coincidence has to be mentioned: K. R. Sreenivasan and C. Menevau studied turbulent jet streams surrounded by quiet liquids. They used a theorem of Helmholz that states, a vortex cannot be stable unless its ends are on solid ground, or with closed ends, forming a torus. A torus is the only known geometrical form where a movement of medium in medium remains stable. They found a fractal dimension of the turbulences with the value of 1,37. This sequence of numbers is the same as the "mysterious" Fine Structure Constant alpha!
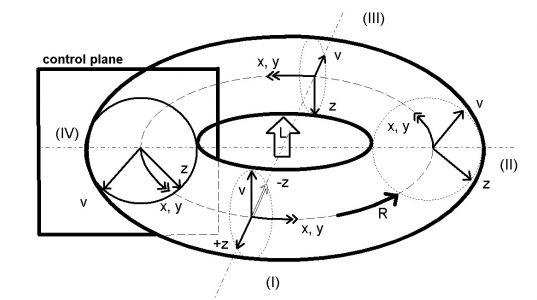
figure 07: a geometric model for electric charge
The torus model for mesons.
The torus as a model for inner quark structure in elementary particles works perfectly for mesons. In the graphic the outer torus has the spin -1/2, the inner one +1/2. Together they become zero. Before it was defined, that the turn around the hub axis represents charge. In this case the myon has no charge. But if both parts of the torus turn in the same direction, the charge will be +1 or -1.
figure 08: a geometric model for mesons
Having two layers, the question comes up, what happens at the contact layers? Studies on turbulent streams lead to the conclusion of fractal torus forms. At the level of particles, the torus stream layer in between the main torus parts could be identified as isospin! The function of the isospin should be similar as with rolls in bearings
figure 09: a geometric model for isospin
With this model it is clear that leptons cannot have isospin. It may be possible that between the iso-spin structure even finer structures are to be found.
If non of the two torus sections are moving, the life time is drastically shorter, as it is the case with *º. With L=0 and R turning in opposite directions (no charge, no spin), the isospin becomes 1. Longer lifetimes are given if the inner and outer torus is moving in the same, and R in the opposite direction, as it is for *+- or *-- particles.
The torus model for baryons.
In the graphic below the three layered torus is used for a model representing the quark structure of a proton. The inner layers run in opposite directions. The spin values one finds on the left side. The directions of the u- und d-quark are on the right side.
A charge unit of a 360 degree turn is 2*. The 120 degree turn of the d-quark enters with 2/3*, and he 240 degree turn of the u-quark is given by 4/3*.
Adding up all spins, the result is +½ -½ +½ = ½.
For the charge units the result is +4/3* -2/3* +4/3* = 2*, that means a full turn with the charge of +1.
Concerning the isospin, one component of it is found between the outer u and the d-quark, the second one is between the inner u and the d-quark. The turning directions are parallel, but in opposing directions. That diminishes the values for the isospin layers fifty percent. Together they make up with ¼ + ¼ = ½.
In case all three spins are going in the same direction, . they add up to 3/2. Then there is no fraction in between the layers, and the isospin becomes zero, as it is with the *¯-particle.
A proton combined with an electron shows up with a zero charge, because the turns of the proton around the axis + Lp and the electron around - Le run in opposite directions. The spins are parallel orientated and turning in opposite directions, thus the layer in between has no turn around the L-axis and the whole object becomes electrically neutral.
Abstract: the fact, that we have no direct experiences with more than three space dimensions should not stop us from studying the possibility of a real existence. For many other objects in science their existence was proofed only indirectly by deduction, or by the effects. This indirect proof is also possible for a real 5-D space. With this hypothesis a lot of problems find a logic explanation. But the most pleasant effect is, it leads to a geometrical model for charge and magnetism that enhances a general understanding of electric forces and the inner structure of particles. In addition, it allows a deduction of the gravitational formula.
Key words: gravitation, quarks, mass formation.
About parity transformation
To imagine space with more than three dimensions is nothing new. Here we draw the conclusions, if space contains real five dimension. Just to go one step further to four real space dimensions would not be valid mathematically, because any space that allows parity transformation must be surrounded by two dimensions higher as the space where the transformation occurs. Nearly two hundred years ago the mathematician Möbius produced for this statement the general proof .
A Necker-cube is am object that produces visually a parity transformation experience in 3-D space. If one looks for a while to the cube skeleton on the left of figure 1(a), it will change in a certain rhythm its appearance. For a while one sees the view like in (b), then for another while like in (c). But these two versions, (b) and (c) are different cubes, like the right and left gloves for hands! If we take for instance the corner E: in (b): the corner A is before E, but in (c) it is in the back! Here a parity conversion occurs in front of our eyes! As it is the same cube when we look at it, the parity transformation turns the inside of the cube outside! In three dimensional space this is not possible, but we can still observe it! That means, we have to ad at least two more dimensions to be in line with he Möbius theorem.

figure 01: the Necker-cube.
A definition of "time"
What kind of laws would be observable if space would have real 5 dimensions?
Before one can study these laws, one has to find a solid definition for the term "time". To start with it, a theorem of Poincaré is used. It proves, that nature changes in quantum steps . With this, the definition of quantum-time is:
"time" is the gap between the appearance of an object, and the exchange by another.
This definition works for all kind of time models, even for human sciences, like psychology and sociology!

figure 02: "time" definition.
With this definition of time, combined with the Einstein-Minkowsky formula, one can create a formula for space with any number of dimensions:
t(sec) x c(m/sec) x i = s(m),
with "t" as the quantum time in seconds, "c" as the constant for light in m/sec, and "i" as the imaginary unit that turns the time vector 90 degrees.
This leads to a model of quantum space.
Now it is possible to create a model for a 4-D space, embedded in a 5-D space. In figure 03 the x and y dimensions of a 3-D space got compressed into one. The point A stands still until it starts moving at time (0), and stops at time point (4). Projected over the time scale, the point describes a kind of s-shape with infinite ends. But one can see it also in a different way: the s-shape is a given object extended in 4-D, and the 3-D-frame moves through 4D. For observers inside the 3-D the results would be the same.

figure03: time and 4-D space
Co-dimension
Normally one needs for the mathematical representation as many equations as there are dimensions. For a space with one hundred dimensions one needs as many equations. But if one observes an object in space, the number on equations is reduced to the difference between the object dimension and the embedding space. So, an object with 99 dimensions in a embedding space of 100 dimensions needs only one equation! Here the term co-dimension is in use. Objects with the same co-dimension have the same features. A 2-D plane divides a 3-D space in two parts, and in an object with the c-dimension 1. Working with co-dimensions becomes interesting, if one does not know exactly how many elements take part, and where the number of elements even can change. Then one talks about fuzzy elements. In general, the basic features of a co-dimension remain, even if one takes off the "superfluous" elements.
An example: a cut of a sphere with a 2-D space creates the co-dimension 3-2=1.
That means, the cut area "C" can be described by one equation, even if it is a multi-dimensional object; C=2r*.
If one considers the existence of higher spaces, then the conclusion is, that the 3-D space-matrix, as we perceive it, can vibrate into the 4-D, like a shaken tapestry into 3-D-sapce. That would add to the longitudinal and transversal waves a third kind of wave pattern, that we can call "matrix-wave". This matrix wave will have effects also inside 3-D objects, because from the 4-D, the inside of 3-D is as open as the inside of a circle can be seen from 3-D ! As an ad-hoc hypothesis one can assume, that the waves of the 4-D-spaces matrix moves with he the so called "sped of light". Later in this paper more proof will be presented to make this hypothesis more probable.
Deduction of the gravitational formula.
In the 5th letter to Newton (Clarke), Leibnitz wrote about the explanation of gravitation by impulse forces . This is not possible with pure 3-D objects in a 3-D only space. But if the objects takes part inside a 4-D space, then the explanation is as easy as follows:
To understand the procedure it is important to remind oneself, that forces from the 4-D-space have effects also on the inside of solid 3-D-objects! Withou this fact, the procedure is not valid, because this represents the fundamental difference to forces in 3-D-space on 3-D objects!
Supposed, the 4-D space is agitated like the waves in a harbor, coming criss-cross from all sides. A single floating object in the water would just remain where it is. It would vibrate, but the average of the impulses coming from the waves would be zeroed out.
The situation changes with a second object in this condition: each object will now block the wave impulses along a line between each other. With time they will come close together! This is the basic idea behind the following deduction for two 3-D objects, T1 and T2 , embedded in a 4-D-space.
Now, the resulting force Fres , through the mutual shielding of T1 and T2 , is caused by the average force Fm of the impulses from the 4-D. Fm can be represented by the density of the impulse field. If the energy density of Fm is rising, under the condition that the rest remains as it is, then the proportion with Fres is lowering. In short: Fm ~ 1/Fres.
Fres ~ 1/Fm. (1)
F1 is the force on the object T1 , and F2 is the force on the object T2 . Then, obviously Fres is proportional with F1 and F2 , because Fres rises if F1 or F2 rises. In short:
Fres ~ F1 and Fres ~ F2 (2)
Taken together, with the proportional constant k we get:
Fres = k F1F2 /Fm (3)
In general terms, one must start with the condition, that both objects are in a moving state. Then one of it can be considered as a relative reference stand still point, and the second as moving relative to the first one.
With m1 for the mass of T1 , m2 for the mass of T2 , and R for the distance of m1 and m2, one needs to insert for the active forces the centripetal laws. Together, with v as the average speed of the quantum impulses from the above mentioned matrix wave field, one gets
F1 = m1v²/R und F2 = m2v²/R (4)
Now we put (4) into (3) and get
Fres. = km1m2v4/FmR² (5).
Next, we unite all constants into one unit K, and kv4/Fm becomes K.
The values of K are: : [m4s2/s4m kg] = [m3/s2kg]
And the formula (5) becomes
Fres. = Km1m2/R² [m3/s2kg] (6)
This equation (6) has exactly the same features and units as the gravitational formula!

figure 04: 4-D gravitation model
anti-gravity
The considerations above imagined a field of impulses from a 4-D space with a certain average frequency. If one could find out this frequency and produce it artificially with a certain intensity, one could enhance the weakened field between the objects and produce anti-gravity.
inertia
This model allows also an explanation of inertia. As the inside of 3-D mass objects are accessible and open from 4-D, the average of the sum of impulses from 4_D are the same if the 3-D object moves steadily or stands still. Acceleration is change of speed, and this needs a new dimension: now the effects of the 4-D-impulses become sensible as we know it from the difference in air or water by through speed changes! The same difference is active for a 3-D-object embedded in 4-D, changing from linear speed to acceleration! The difference is only, that for a 3-D-object in 3-D space the air resistance depends on the surface, but for the acceleration of a 3-D object embedded in a 4-D space it depends on all particles of the object, also those that are found inside.

figure05: inertia model
The torus as a spin model for elementary particles
So far, science uses as a model for particles spheres. If our visible and touchable 3-D-objects would be part of a higher dimensional real existing space, then another model would also be possible: a 4-D-hyper-torus. A torus has a very particular feature, that sets it apart from all other objects: it can contain two independent rotary axes. A bicycle tube is a good example to understand the principles: The bike tube has a valve, that we will use as a reference point. Usually it is mounted in a way, that it points towards the bicycle hub. Now, the tube can turn around the hub H, then the valve points always inside. But the tube can also turn around its middle axis A! Then it turns from the inside out and back inside. These two ways of turns are totally independent!
That means, any kind of combination is possible. Let us start with the easiest: the tube moves in a way, that for a 360 degree turn around H the valve turns 180 degrees around A. Another 360 degree turn around H is needed, before the valve and all other particles of the bike tube are in the original position.
The proportion of the two turns A and H are then ½. Obviously, with this model all kind of proportions are possible! This feature of a torus makes it a perfect model for explaining spin for elementary particles!
Each of the two turning axes A and H of the torus can be in one of the three kind of states, two moving ones and one stand still. That makes up to a 9-fold pattern of 8 moving combinations, and one with zero movement.

figure 06: torus dynamic combination table
J. A. Wheeler showed also a connection between spin ½ and the torus. He explains it using a projection of a 4-D hyper-cube, where the corners of two cubes are connected by lines. Turning one of these cubes two times 360 degrees will twist the strings. If we turn now the twisted cube around the other, the strings will be free again! As a very simple experiment one can take a stiff belt and fix one end on the table. The four edges of the belts represent the four strings. Now the free end of the belt gets twisted two times 360 degrees. Then the twisted free end has to be turned around the fixed end, keeping the orientation. As a result the twist disappears! But this does not work if the belt gets twisted only one time 360 degrees!
The torus model and charge
For an easier understanding, the torus in the graphic shows at the center an opening. But for the following calculation a torus with no opening is considered!
During one turn the center of the torus covers the distance 2r*, that will be ad-hoc identified with the electric charge Q: 2r* = Q.
A torus with no hole inside has a surface of 2r*.
So, the whole surface that moves through the control area in one turn is
4*2r2 = Q².
Above is mentioned, that the propagation of the 4-D-wave pattern follows the speed of light c. In case, the turns of the torus are proportional with this pattern, then we have to divide the charge by c, getting Q²/c. For quantum objects we also have to divide this with the Heisenberg Constant h/2*, and we will get 2*Q²/ch. If we set for Q the charge of an electron, the result is the Fine-Structure-Constant Alpha!
An interesting coincidence has to be mentioned: K. R. Sreenivasan and C. Menevau studied turbulent jet streams surrounded by quiet liquids. They used a theorem of Helmholz that states, a vortex cannot be stable unless its ends are on solid ground, or with closed ends, forming a torus. A torus is the only known geometrical form where a movement of medium in medium remains stable. They found a fractal dimension of the turbulences with the value of 1,37. This sequence of numbers is the same as the "mysterious" Fine Structure Constant alpha!

figure 07: a geometric model for electric charge
The torus model for mesons.
The torus as a model for inner quark structure in elementary particles works perfectly for mesons. In the graphic the outer torus has the spin -1/2, the inner one +1/2. Together they become zero. Before it was defined, that the turn around the hub axis represents charge. In this case the myon has no charge. But if both parts of the torus turn in the same direction, the charge will be +1 or -1.

figure 08: a geometric model for mesons
Having two layers, the question comes up, what happens at the contact layers? Studies on turbulent streams lead to the conclusion of fractal torus forms. At the level of particles, the torus stream layer in between the main torus parts could be identified as isospin! The function of the isospin should be similar as with rolls in bearings

figure 09: a geometric model for isospin
With this model it is clear that leptons cannot have isospin. It may be possible that between the iso-spin structure even finer structures are to be found.
If non of the two torus sections are moving, the life time is drastically shorter, as it is the case with *º. With L=0 and R turning in opposite directions (no charge, no spin), the isospin becomes 1. Longer lifetimes are given if the inner and outer torus is moving in the same, and R in the opposite direction, as it is for *+- or *-- particles.
The torus model for baryons.
In the graphic below the three layered torus is used for a model representing the quark structure of a proton. The inner layers run in opposite directions. The spin values one finds on the left side. The directions of the u- und d-quark are on the right side.
A charge unit of a 360 degree turn is 2*. The 120 degree turn of the d-quark enters with 2/3*, and he 240 degree turn of the u-quark is given by 4/3*.
Adding up all spins, the result is +½ -½ +½ = ½.
For the charge units the result is +4/3* -2/3* +4/3* = 2*, that means a full turn with the charge of +1.
Concerning the isospin, one component of it is found between the outer u and the d-quark, the second one is between the inner u and the d-quark. The turning directions are parallel, but in opposing directions. That diminishes the values for the isospin layers fifty percent. Together they make up with ¼ + ¼ = ½.
In case all three spins are going in the same direction, . they add up to 3/2. Then there is no fraction in between the layers, and the isospin becomes zero, as it is with the *¯-particle.
A proton combined with an electron shows up with a zero charge, because the turns of the proton around the axis + Lp and the electron around - Le run in opposite directions. The spins are parallel orientated and turning in opposite directions, thus the layer in between has no turn around the L-axis and the whole object becomes electrically neutral.
-
nicole6

- ModeratorIn

- Beiträge: 2333
- Registriert: 11.09.2009, 13:01
- Wohnort: München
- Ich bin: ehemalige SexarbeiterIn
RE: Diskussionspapier: Modell für Zeit und Raum
figure 10: a geometric model for a proton
In general, charged particles are a little bit heavier as uncharged ones. The neutron is no exception to this, even if it seems paradox because of its nomination! It carries even two charges: one of the proton, and one of an electron. The third particle in between them is an electron-anti-neutrino. The torus model below could be a geometric outer representation of a neutron. The inside structure is as in figure 10.
figure 11: a geometric model for a neutron
This torus model allows also an explanation why protons and neutrons are very stable. The quark layers inside have a frequency proportion of 3/2. This number shows also up in astronomy. Usually parts of the asteroid belt are found in higher numbers where less changes of gravitational forces occur. On places with lots of changes one finds only few objects. Those gaps one finds at proportions like 2:1, 3:1, 4:1, 5:2 and 7:2. But an exception is at 3:2, called the Hilda-group. That means, this proportion carries particular features. Computer simulations for a period of over 100 million years show, that the 3:2 proportion is stable!
A hypothesis for mass formation.
Studies of tornados show that towards the vortex center the speed of the tube drops very fast towards zero. The good visibility of a tornado is caused by adiabatic cooling, when high pressure differences induce condensation of air humidity. An analog pattern could work when a 4-D energy field forms a dynamic torus shape. At the center inside the torus the energy could "condense" into mass by an analogical process as the adiabatic cooling effect. The condensed energy could remain stable in the same way as frozen water remains stable for a long time. Protons and neutrons might contain such a condensed nucleus of energy, better known as "mass", at the center of the surrounding torus pattern.
The involvement of the torus shape is probable also by another feature. As energy is quantisized, it has to follow certain rules of discrete chaos dynamic. To reach stable forms, an attractor is needed. Poincaré mentioned, that in 3-D space the torus offers the highest probability for an attractor.
The weak force and the torus
To understand the following graphic in the right way, I must remember, that it is a 4-D-model!
The intersection of a 4-D torus with a 3-D space appears as one sphere!
As a conventional rule the clockwise turn of the central torus axis will represent the positive charge (L3), the other direction stands for the negative one (L1 and L2).
In a shell electrons can be paired only with opposing spin. Supposed there is an energy connection between the nucleus and the electrons. If all participating objects have dynamic torus shapes, it can only happen in the way as it is shown in figure 12. One of the energy bridges must link up from the top, the other from the bottom of the nucleus torus. But this connection is not symmetrical! Due to the dynamic torus pattern the "upper" connection of the left handed electron will be wider as the "lower" one, because the energy handle from the right handed electron will be pulled inside the torus center. In this way the energy bridge of the right handed electron becomes physically smaller, and as a result it will have a higher energy density!
figue 12: a model for symmetry breaking
If a group of atoms find themselves inside a strong magnetic field, they will all be orientated. Then, the probability that the left handed electron of the upper link is breaking apart, will be higher as for the lower one. This might be the reason for the result of the experiment of Mrs. Wu and her collaborators 1956 at the University of New York, when they observed the decay of the Cobalt isotope 60 with 30% more left-handed Electrons.
The gyroscope
In the following figure 13 a horizontal turning disk, balanced on a tip, is counter weighted on the other side. If one puts an additional weight K on the left side, the axis does not go up, as it would be if the disk does not turn, but it starts to turn horizontally counter clock wise. With the hypothesis of a real existing 4-D, it is easy to explain. The reason for this effect has the same roots as inertia!
As long as the gyroscope is turning, any positional change causes a change of impulse towards the 4-D, as the 4th dimension is rectangular to all three dimensions of the 3-D! That makes he gyroscope stable. An additional weight K on the left side lifts the turning wheel on the right side up, inducing friction from the 4-D. It is, as if then on top a kind of solid mass appears, where the wheel will roll along. Consequently the axis must turn counter clock wise!
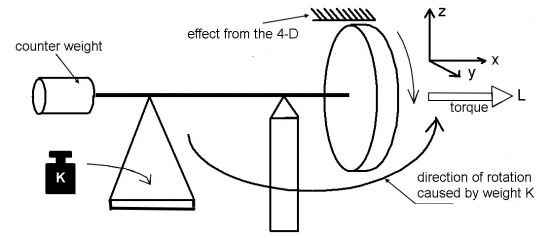
figure 13: the gyroscopic effect and 4-D
Neutral current effects in nuclei
With the torus as a model, a neutrino does not turn around the central hub axis, but only around the tube axis. As a result it does not carry charge, because with this model, charge means turn around the hub. In case a neutrino hits an object, the neutrino torus receives an impulse and starts turning, what can be measured as charge (case 2 in figure 14). But in those few cases where the neutrino hits the object perpendicular (case 1 in figure 14), there will be no horizontal energy input, and the neutral appearance of the neutrino remains. As these events happen in regions where quantum laws reign, there will be a certain leeway for the deviation from the exact rectangular angle.